Equation de Kepler hyperbolique

Auteur : Marc Fouchard.

Le but de cet exercice est de résoudre l'équation de Kepler dans le cas hyperbolique. On a déjà vu ici comment résoudre l'équation de Kepler dans le cas elliptique. On va voir ci une méthode similaire pour une trajectoire hyperbolique. Dans ce cas l'équation de Kepler est :

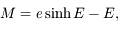
où 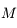est l'anomalie moyenne, 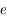est l'excentricité (qui est 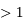dans le cas hyperbolique) et 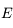est l'anomalie excentrique. On peut voir ici une animation avec le lien entre les trois anomalies dans le cas hyperbolique. ( 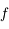correspond à l'anomalie vraie)