Univers à courbure négative

Auteur: Jérôme Thiébaut

Les équations d'Einstein de la relativité générale appliquées à l'univers que l'on suppose être un fluide homogène et isotrope, aboutissent à l'équation de Friedmann,

,

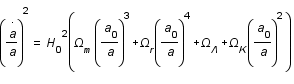décrivant l'évolution de l'univers en fonction de son contenu. Ce contenu est défini par les paramètres de densité de matière, 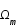, de rayonnement, 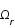, de constante cosmologique, 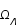et de courbure, 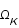. 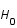est la constante de Hubble et 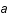est le facteur d'échelle décrivant l'évolution de l'univers. La composition de l'univers évoluant avec le temps, les différents paramètres de densité ont des importances relatives différentes en fonction de l'ère cosmologique considérée. 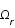Ils sont tour à tour dominants ( puis 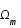et 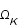et enfin 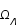) ou négligeables. On se propose dans cet exercice d'étudier un modèle d'univers dominé par la matière avec une courbure négative et de vérifier si il peut coïncider avec les observations actuelles.