Ex: désintégration radioactive

Auteurs: Alain Vienne, Stéphane Erard

Auteur: Stéphane Erard

Désintégration radioactive

Difficulté : ☆ Temps : 15 min

Question 1)

On considère une seule espèce radioactive. Soit N(t) le nombre d'atomes à l'instant t, quel est le nombre de désintégrations dN pendant l'intervalle de temps dt ?

Aide Solution

Question 2)

En déduire le nombre d'atomes présents à l'instant t.

Aide Solution

Question 3)

Au bout de quel intervalle de temps 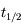$t_{1/2}$ le nombre d'atomes radioactifs est-il réduit de moitié ?

Tracer la courbe d'évolution et sa tangente à l'instant initial. Reporter 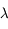$\lambda$ et $t_{1/2}$ .

Solution

Question 4)

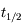On définit l'activité A comme le nombre de désintégrations par seconde d'une espèce. C'est une grandeur observable, qui se mesure en Becquerels (Bq) dans le Système International. Exprimer celle-ci en fonction du temps.

Solution

Auteur: Stéphane Erard

Datation de météorites

Difficulté : ☆ Temps : 30 min

On utilise la loi de décroissance radioactive pour dater un échantillon de météorite. Les âges étant élevés (de l'ordre de l'âge du Système solaire, ~5 milliards d'années) on utilise des isotopes à longue période.

Le rubidium 87 décroît par radioactivité 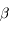$\beta$ en strontium 87 avec une demi-vie de 49 milliards d'années, selon la réaction suivante :

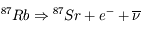
$^{87} Rb \Rightarrow ^{87} Sr + e^- + \overline{\nu}$

Un des neutrons se transforme en proton (radioactivité 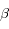$\beta$ ). Le nombre de masse (87) est inchangé, le nombre de charges varie (de 37 à 38). La charge totale est conservée par l'émission d'un électron. La quatrième particule est un anti-neutrino symétrique de l'électron, dont la présence est requise par la conservation du moment cinétique.

Question 1)

Ecrire la quantité de 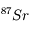$^{87} Sr$ à l'instant de la mesure t en fonction des quantités de 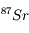$^{87} Sr$ initiale et de 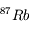$^{87}Rb$ actuelle et initiale.

Solution

Question 2)

Récrire cette équation pour éliminer une des quantités inconnues.

En pratique, on mesure des rapports d'abondance ; en l'occurrence on rapporte toutes les abondances à celle du 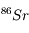$^{86} Sr$ , isotope stable du strontium qui n'est pas un produit de désintégration (son abondance n'est donc pas fonction du temps). Faire apparaître ces rapports. Commentaires ?

Solution

Question 3)

On lève l'indétermination précédente en effectuant cette mesure sur différents minéraux présents dans la même météorite, et formés au même moment. Reporter les points de mesures attendus sur un graphique dérivé de la fonction précédente.

Aide Solution

Question 4)

Les mesures des rapports isotopiques dans l'exemple sont les suivantes :

Rapports isotopiques
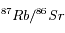
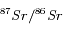
$^{87}Rb/^{86}Sr$	$^{87}Sr/^{86}Sr$
0.059	0.703
0.137	0.708
0.158	0.709
0.295	0.718
0.323	0.720
0.376	0.724
0.386	0.724

Trouver un ordre de grandeur de l'âge de la météorite à l'aide des chiffres fournis. Que mesure-t-on exactement avec cette méthode ?

Aide Solution