 |  |  |  |  |  |
Ex: Univers à courbure négative |
Univers à courbure négativeDifficulté : ☆☆ Temps : 30 mn
On considère un univers dominé par la matière non relativiste et avec une courbure négative. Dans ce cas, l'équation de Friedmann s'écrit:
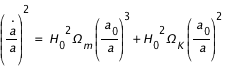
où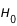 
est la constante de Hubble, 
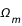le paramètre de densité et 
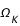le paramètre de courbure.
La solution sous une forme paramétrique est:
, 
,
où 
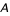et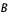 
sont des constantes.
Dériver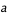 
et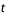 
par rapport au temps et éliminer la dépendance en 
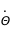de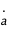 
.
Calculer les constantes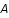 
et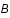 
comme fonction de la constante de Hubble et des paramètres de densité et de courbure.
Calculer le paramètre de décélération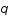 
défini comme: 
.
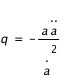Les observations actuelles montrent que l'univers est dans une phase d'accélération. Ce type d'univers a t'il une phase accélérée ? Peut-il représenter notre univers ?
 |  |
,
,
.
,
.
et
.
et 
.
Le paramètre de décélération étant toujours positif, ce type d'univers n'a pas de phase d'accélération. Il n'est donc pas compatible avec le nôtre puisque nous sommes dans une phase d'expansion accélérée.