 |  |  |  |  |  |
Ex: équation de Kepler hyperbolique |
équation de Kepler hyperboliqueDifficulté : ☆☆ Temps : 1h
Soit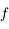 
la fonction définie par 
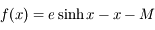sur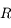 
avec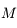 
une constante. Montrer que 
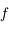est continue dérivable 2 fois, que 
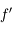est strictement supérieure à zéro et que 
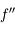est supérieure à zéro pour 
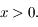On rappelle que dans le cas hyperbolique 
.
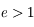Soit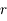 
, le nombre réel positif tel que 
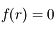. Montrer que pour 
, 
.
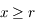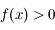Montrer que la courbe représentative de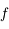 
est au-dessus de sa tangente sur 
.
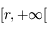En déduire que la suite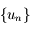 
converge et que sa limite est 
.
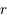Cette propriété de la suite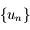 
est utilisée pour résoudre par itération et de manière approchée l'équation de Kepler.
 |  |
est continue, dérivable deux fois sur 
.
. Pour tout 
, 
. Comme 
on en déduit que 
pour 
.
. Pour 
on a donc bien 
.
est strictement croissante sur 
. Comme 
et que 
on a bien 
, on a:
![g(x)=f(x)-[f(x_0)+f'(x_0)(x-x_0)]](../pages_hyper/equations_hyper/equation79.png)
.
et 
. Ainsi 
est une fonction croissante au voisinage de 
, donc 
est négative pour 
et positive pour 
. Donc 
correspond à un minimum pour 
. Ainsi au voisinage de 
on a 
ce qui montre que la courbe représentative de 
est effectivement au-dessus de sa tangente.
définie par:
, est décroissante et minorée par 
.
et 
sont positives sur 
, la suite 
est effectivement décroissante tant que les valeurs de la suite restent dans 
.
D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse 
est le point d'intersection de la tangente au point d'abscisse 
à la courbe représentative de 
avec l'axe des abscisses, on en déduit que 
puisque la tangente est en-dessous de la courbe représentative de 
. Comme 
est croissante et que 
on a bien 
.
étant décroissante et minorée par 
elle converge vers une limite 
. A la limite on a :
,
. Ainsi on a bien 
.