L'Astronomie dans l'apprentissage des Mathématiques
L'Astronomie dans l'apprentissage des Mathématiques
Entrée du siteSommaireGlossairePage pour l'impression<-->
- Les réels et les suites
- Suites réelles
• Equation de Kepler elliptique
• Ex: equation de Kepler elliptique

Ex: equation de Kepler elliptique
Auteur: Marc Fouchard
Auteur: Marc Fouchard
calcotron

exerciceéquation de Kepler elliptique

Difficulté : ☆   Temps : 30 mn

Question 1)

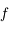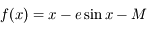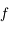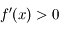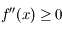Soit f la fonction définie par f(x)=x-e\sin x -M, avec M \in [0;2\pi] une constante. Montrer que f est continue, dérivable deux fois et que f'(x)>0 et pour x\in [0;\pi] , f''(x)\ge 0.

Solution

Question 2)

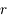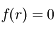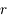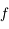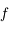Soit r le nombre réel tel que f(r)=0 (on peut montrer rapidement que r existe d'après la continuité de f et le théorème de la valeur intermédiaire). Montrer que pour x\in]r;\pi], f est strictement positive.

Solution

Question 3)

Montrer que la courbe représentative de 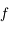f est au dessus de sa tangente sur [r;\pi].

Solution

Question 4)

En déduire que la suite 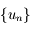\left\lbrace u_n \right\rbrace définie par:

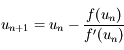u_{n+1}=u_n-\frac{f(u_n)}{f'(u_n)},

avec 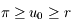\pi\ge u_0 \ge r, est décroissante et minorée par r.

Solution

Question 5)

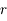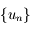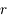En déduire que la suite \left\lbrace u_n \right\rbrace converge et que sa limite est r.

Solution

Page précédentePage suivante