Auteur: Marc Fouchard
 loi de Stefan
loi de Stefan
Difficulté : ☆☆
Temps : 1h
Question 2)
L'énergie totale 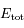 est donnée par :
est donnée par :
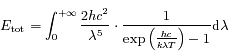 .
.
Montrer, en effectuant un changement de variable approprié, que 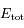 peut s'écrire sous la forme:
peut s'écrire sous la forme:
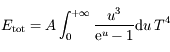
où 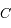 est une constante que l'on déterminera.
est une constante que l'on déterminera.
On pourra faire le changement de variable 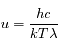 .
.
Question 3)
Montrer que l'intégrale
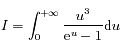
est convergente.
 Remarque
Remarque
Cette intégrale est une fonction zeta de Reimann. On peut montrer que 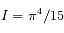 .
.
Question 4)
En déduire la loi de Stefan:
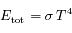
où 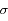 est une constante que l'on déterminera.
est une constante que l'on déterminera.
Auteur: Stéphane Erard
On considère un gaz en équilibre, pour lequel on veut connaître les vitesses des molécules. La théorie cinétique des gaz ne donne qu'une valeur moyenne (la vitesse quadratique moyenne) :
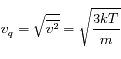
où m est la masse des molécules, T est la température, k la constante de Boltzman.
On cherche ici la distribution de vitesse, c'est-à-dire la probabilité d'avoir une vitessse comprise entre v et v+dv. Le calcul qui suit est classique (non quantique) et reproduit l'étude de Maxwell au XIXe siècle.
Auteur: Stéphane Erard
 Intégrales gaussiennes
Intégrales gaussiennes
Difficulté : ☆☆
Temps : 60 min
Le calcul des propriétés de la loi normale suppose l'intégration de la fonction gaussienne, et des intégrales similaires apparaissent dans le calcul suivant.
Le moment d'ordre n de la loi normale réduite (de moyenne nulle) est :
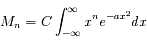
où a > 0 et n ≥ 0, C étant une constante de normalisation. On s'intéresse ici à :
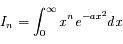
Question 1)
Trouver une relation de récurrence entre les intégrales 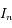 .
.
On intègre par partie en posant
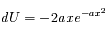
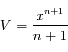
Question 2)
Calculer 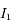 . Que représente cette quantité ?
. Que représente cette quantité ?
Question 3)
Calculer l'intégrale de Gauss 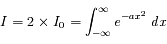
Question 4)
En déduire les moments de la loi normale centrée.
Auteur: Stéphane Erard
 Distribution des vitesses
Distribution des vitesses
Difficulté : ☆☆
Temps : 60 min
La probabilité pour qu'une molécule ait une vitesse comprise entre 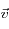 et
et 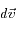 est notée
est notée 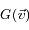 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
Question 1)
Ecrire les conditions d'indépendance entre les composantes du vecteur vitesse, et d'isotropie.
Question 2)
En déduire la forme de G.
Question 3)
Identifier deux conditions qui permettent de calculer les coefficients ci-dessus.
Question 4)
Calculer les intégrales 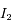 et
et 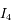 de l'exercice précédent.
de l'exercice précédent.
Question 5)
En dériver l'expression de 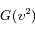 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
Question 6)
En dériver l'expression de 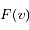 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.
Question 7)
Tracer cette fonction, expliquer sa forme.
Question 8)
Comment peut-on utiliser cette fonction pour expliquer l'évolution des atmosphères planétaires ?
Auteur : S. Renner
On estime ici la durée de vie d'une étoile de type solaire, en supposant tout d'abord que la seule source d'énergie est la gravitation, puis en considérant le cas réel des réactions de fusion thermonucléaire de l'hydrogène en hélium. La première hypothèse (dissipation de l'énergie gravitationnelle) est une idée qui apparaît avec les travaux de Kelvin au XIXe siècle.
Auteur: S. Renner
 Temps de vie d'une étoile
Temps de vie d'une étoile
Difficulté : ☆
Temps : 1h
On assimile l'étoile à une sphère homogène de masse 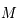 et de rayon
et de rayon 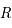 .
.
Question 1)
Montrer que son énergie de liaison gravitationnelle est 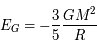 .
.
On considérera le travail élémentaire 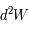 d'une couronne sphérique d'épaisseur
d'une couronne sphérique d'épaisseur 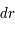 .
.
L'énergie de liaison gravitationnelle sera alors donnée par 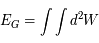 , en prenant les bornes d'intégration adéquates.
, en prenant les bornes d'intégration adéquates.
Question 3)
Même question en considérant le cas réel des réactions de fusion nucléaire de l'hydrogène en hélium au coeur du Soleil. On suppose que 10% de la masse 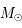 est convertie en hélium et que la luminosité
est convertie en hélium et que la luminosité 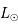 reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie
reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie 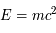 .
.
Question 4)
Le Soleil brille depuis 4.5 milliards d'années. Combien a t-il perdu en masse ?
-
Question 1
Solution :
En posant 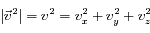
l'indépendance entre composantes de vitesse s'écrit :
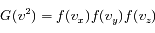
L'isotropie se traduit par :
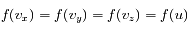 Soit :
Soit : 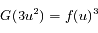
On peut donc écrire :
![G(v_x^2+v_y^2+v_z^2) = \left[G(3v_x^2) G(3v_y^2) G(3v_z^2)\right]^{1/3}](../pages_int-gen/equations_int-gen/equation66.png)
-
Question 2
Solution :
On prend le logarithme et on pose 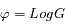 :
:
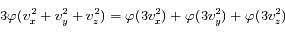
C'est la définition d'une fonction linéaire. On a donc :
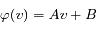
Soit
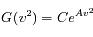
-
Question 3
Solution :
G est une densité de probabilité, elle est donc normalisée :
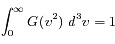
Par ailleurs on connaît la vitesse quadratique moyenne :
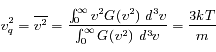
-
Question 4
Solution :
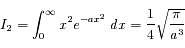
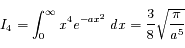
-
Question 5
Solution :
La condition de normalisation est :
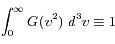
où 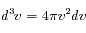 en coordonnées sphériques. Ceci donne :
en coordonnées sphériques. Ceci donne :
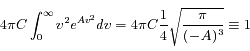
La vitesse quadratique moyenne donne :
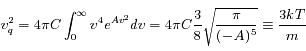
Le rapport des deux conditions conduit à :
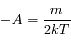 d'où
d'où 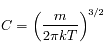
On en conclut :
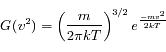
-
Question 6
Solution :
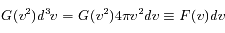
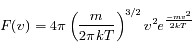
qu'on appelle distribution de Maxwell-Boltzman.
-
Question 7
Solution :
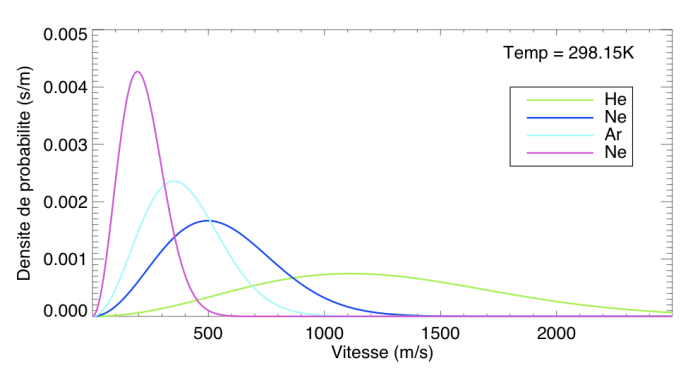
Distributions de Maxwell pour différents gaz rares à température ambiante.
Le maximum de la fonction n'est pas dû à la gaussienne elle-même (il est loin de la moyenne de celle-ci qui est centrée), mais au produit de la queue de la gaussienne par un polynôme de degré 2.
-
Question 8
Solution :
En utilisant la température qui règne au sommet de l'atmosphère, la fonction permet de calculer la distribution de vitesse des différentes espèces moléculaires ou atomiques. On peut comparer celle-ci à la vitesse d'échappement de la planète, qui dépend de sa gravité et de son rayon (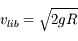 ).
).
Si une fraction significative des molécules a une vitesse supérieure à la vitesse de libération, cette espèce s'échappera rapidement de la haute atmosphère — c'est la raison première pour laquelle la Lune n'a pas d'atmosphère, alors que la Terre conserve la sienne à la même distance du Soleil.
En dehors de ce mécanisme d'échappement thermique, il existe d'autres mécanismes d'échappement atmosphérique.
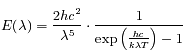
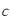 correspond à la vitesse de la lumière dans le vide,
correspond à la vitesse de la lumière dans le vide, 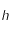 est la constante de Planck,
est la constante de Planck, 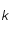 la constante de Boltzmann,
la constante de Boltzmann, 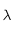 la longueur d'onde à laquelle le rayonnement est émis et
la longueur d'onde à laquelle le rayonnement est émis et 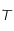 la température de surface du corps noir.
la température de surface du corps noir.
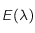 pour différente température de surface du corps noir. Sachant que l'énergie totale
pour différente température de surface du corps noir. Sachant que l'énergie totale 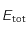 émise par le corps noir par seconde et par unité de surface correspond à l'aire comprise en l'axe des abcisses et la courbe, on remarque que
émise par le corps noir par seconde et par unité de surface correspond à l'aire comprise en l'axe des abcisses et la courbe, on remarque que 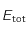 augmente avec la température de surface du corps noir (il ne faut pas cocher la case "normaliser").
augmente avec la température de surface du corps noir (il ne faut pas cocher la case "normaliser").
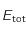 et la température de surface
et la température de surface 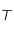 du corps noir.
du corps noir.

 Remarque
Remarque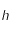 ,
, 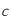 et
et 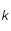 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 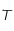 étant mesurée en degré Kelvin est aussi strictement positive, montrer que
étant mesurée en degré Kelvin est aussi strictement positive, montrer que 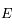 est de classe
est de classe 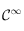 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation18.png) et est toujours strictement positive sur cet intervalle.
et est toujours strictement positive sur cet intervalle.
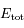 est donnée par :
est donnée par :
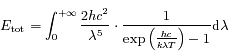 .
.
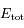 peut s'écrire sous la forme:
peut s'écrire sous la forme:
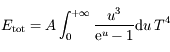
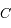 est une constante que l'on déterminera.
est une constante que l'on déterminera.
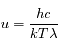 .
.
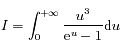
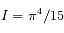 .
.
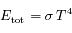
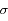 est une constante que l'on déterminera.
est une constante que l'on déterminera.
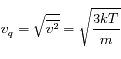
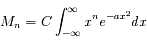
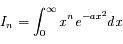
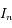 .
.
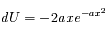
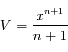
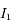 . Que représente cette quantité ?
. Que représente cette quantité ?
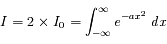
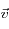 et
et 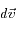 est notée
est notée 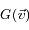 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une 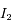 et
et 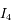 de l'exercice précédent.
de l'exercice précédent.
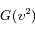 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
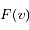 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.
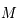 et de rayon
et de rayon 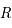 .
.
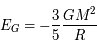 .
.
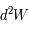 d'une couronne sphérique d'épaisseur
d'une couronne sphérique d'épaisseur 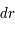 .
.
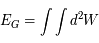 , en prenant les bornes d'intégration adéquates.
, en prenant les bornes d'intégration adéquates.
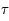 du Soleil sur ses seules ressources gravitationnelles. On rappelle que la luminosité (puissance totale rayonnée) du Soleil est
du Soleil sur ses seules ressources gravitationnelles. On rappelle que la luminosité (puissance totale rayonnée) du Soleil est 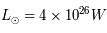 , sa masse
, sa masse 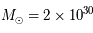 kg et son rayon
kg et son rayon 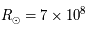 m.
m.
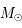 est convertie en hélium et que la luminosité
est convertie en hélium et que la luminosité 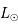 reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie
reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie 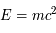 .
.
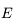 s'écrit comme un produit de fonctions ou de composition de fonctions qui sont de classe
s'écrit comme un produit de fonctions ou de composition de fonctions qui sont de classe 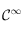 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation21.png) , donc
, donc 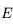 est aussi de
classe classe
est aussi de
classe classe 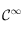 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation24.png) . Le signe s'optient de la même manière, en considérant le signe de chaque fonction intervenant dans le calcul de
. Le signe s'optient de la même manière, en considérant le signe de chaque fonction intervenant dans le calcul de 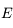 sur cet intervalle.
sur cet intervalle.
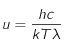 .Ainsi
.Ainsi 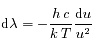 , et en substituant dans l'expression de
, et en substituant dans l'expression de 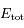 on obtient:
on obtient:
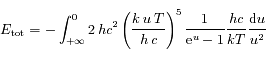 ,
,
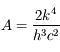 .
.
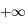 l'intégrande est équivalente à
l'intégrande est équivalente à 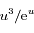 , dont l'intégrale converge en
, dont l'intégrale converge en 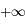 puisque l'exponentielle l'emporte sur tout polynôme;
puisque l'exponentielle l'emporte sur tout polynôme; 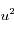 , dont l'intégrale converge 0
, dont l'intégrale converge 0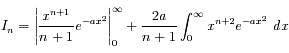
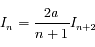
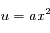 on trouve :
on trouve :
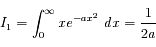
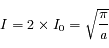
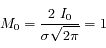 (normalisation de la densité de probabilité).
(normalisation de la densité de probabilité).
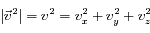
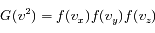
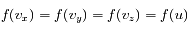 Soit :
Soit : 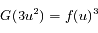
![G(v_x^2+v_y^2+v_z^2) = \left[G(3v_x^2) G(3v_y^2) G(3v_z^2)\right]^{1/3}](../pages_int-gen/equations_int-gen/equation66.png)
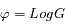 :
:
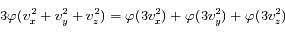
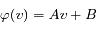
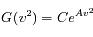
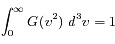
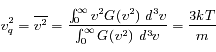
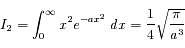
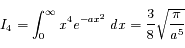
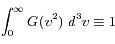
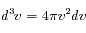 en coordonnées sphériques. Ceci donne :
en coordonnées sphériques. Ceci donne :
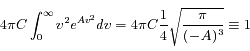
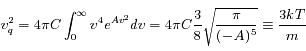
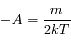 d'où
d'où 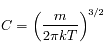
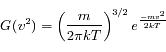
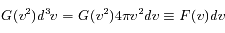
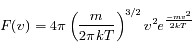

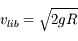 ).
).
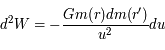
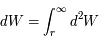
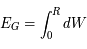
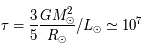 ans.
ans.
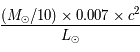 = 10 milliards d'années.
= 10 milliards d'années.
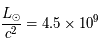 kg/s.
kg/s.
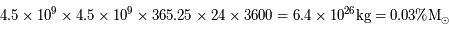 .
.