Auteur: Alain Vienne
Lors de la découverte d'un nouvel objet dans le système solaire, on souhaite rapidement connaitre sa trajectoire. Celle-ci est généralement héliocentrique et, dans un premier temps, on la suppose képlérienne. Or les observations terrestres donnent uniquement la direction de l'astre mais pas sa distance. La méthode de Laplace propose un moyen qui, à partir de 3 observations de direction faites à des dates assez rapprochées, donne les vecteurs position et la vitesse de l'astre. Le détail de la méthode peut être vu dans le cours suivant: Dynamique du système solaire. On peut y voir notamment que la méthode conduit à chercher les racines d'un polynôme de degré 8.
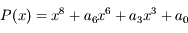
Il y est affirmé qu'il y a 4 racines réelles (1 négative, 3 positives) et 4 complexes non réelles. Cette affirmation est étudiée et montrée dans l'exercice Les racines du polynôme de la méthode de Laplace. Ici, on montre que 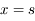 où
où 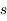 est la distance Terre-Soleil, et, on utilise cette racine pour factoriser le polynôme.
est la distance Terre-Soleil, et, on utilise cette racine pour factoriser le polynôme.
Voici à titre d'exemple le graphe du polynôme dans le cas de 3 observations de Jupiter à son opposition (courbe "complète" et un agrandissement):
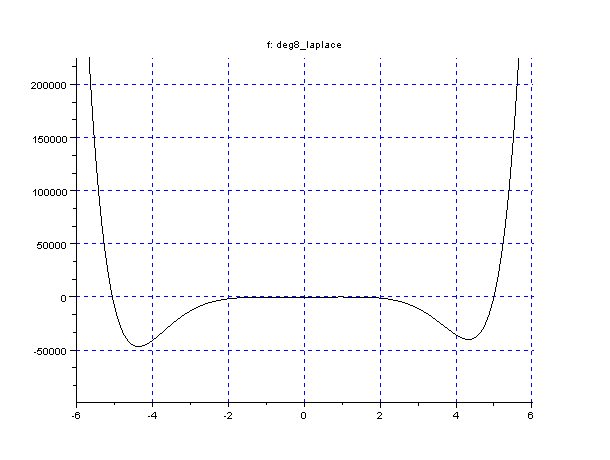
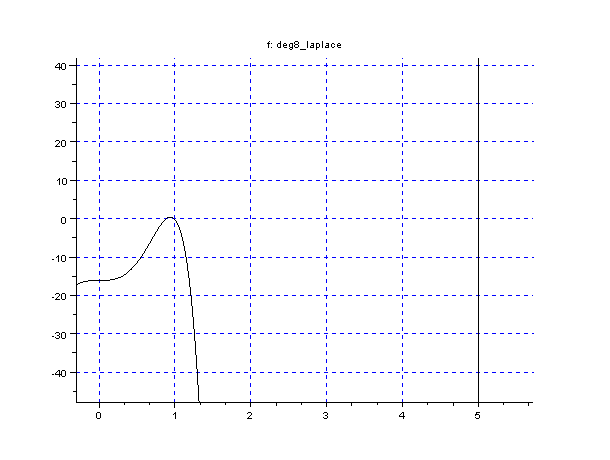
Le polynome de la méthode de Laplace dans le cas de 3 observations de Jupiter (courbe "complète" et un agrandissement). L'axe horizontal est gradué en ua. On note que ce polynôme n'est pas très bien conditionné car la vue d'ensemble ne donne pas une idée des racines ni même du nombre de ces racines. La deuxième figure est agrandissement sur la partie utile. On note la racine
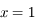
ua (
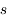
) et les 2 autres racines dont celle à 5 ua.
Auteur: Alain Vienne
 Factorisation du polynôme de la méthode de Laplace
Factorisation du polynôme de la méthode de Laplace
Difficulté : ☆
Temps : 30mn
Le polynôme issu de la méthode de Laplace a la forme suivante:
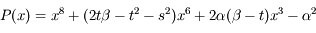
où 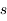 est la distance Terre-Soleil et
est la distance Terre-Soleil et 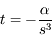 .
.
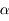 et
et 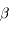 sont des coefficients réels issus de la géométrie du problème.
sont des coefficients réels issus de la géométrie du problème.
Question 1)
Vérifier que 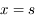 est racine de
est racine de 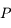 .
.
Question 2)
Mettre en facteur 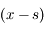 dans
dans 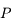 .
.
Faire le changement de variables 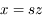 pour éliminer les fractions.
pour éliminer les fractions.
Auteur: Alain Vienne
En Mécanique Céleste, on est souvent conduit à utiliser les polynômes de Legendre que l'on note ici 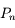 .
.
C'est le cas, par exemple, dans le développement du potentiel terrestre. Si on suppose que la Terre est un sphéroïde, le potentiel peut s'écrire:
![U(r,\varphi)=\frac{KM_T}{r} \ [1 - \sum_{m=1}^{\infty} J_{2m} (\frac{a_e}{r})^{2m} P_{2m}(\sin\varphi) \ ]](../pages_poly/equations_poly/equation23.png)
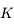 est la constante de gravitation de la Terre,
est la constante de gravitation de la Terre, 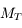 la masse totale de la Terre,
la masse totale de la Terre, 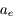 son rayon équatorial et
son rayon équatorial et 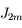 des coefficients numériques.
des coefficients numériques. 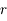 et
et 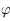 sont le rayon et la latitude du point pour lequel on évalue le potentiel
sont le rayon et la latitude du point pour lequel on évalue le potentiel 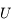 .
.
Un autre exemple d'utilisation est de considérer 2 corps 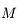 et
et 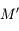 décrivant autour d'un centre
décrivant autour d'un centre 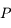 des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre
des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre 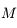 et
et 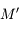 , on doit écrire l'inverse de la dsitance entre
, on doit écrire l'inverse de la dsitance entre 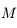 et
et 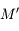 ,
, 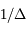 , en fonction de leurs éléments d'orbite. On montre facilement que:
, en fonction de leurs éléments d'orbite. On montre facilement que:
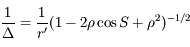
Avec 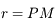 ,
, 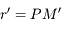 ,
, 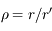 et
et 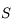 l'angle entre
l'angle entre 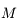 et
et 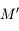 vu de
vu de 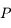 .
.
Cette dernière expression est développée en puissance de 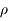 grâce aux polynômes de Legendre:
grâce aux polynômes de Legendre:
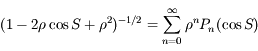
Ce développement est rapidement convergent si 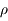 est petit. C'est le cas si, par exemple,
est petit. C'est le cas si, par exemple, 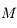 est la Terre,
est la Terre, 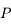 le Soleil et
le Soleil et 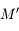 un satellite artificiel.
un satellite artificiel.
Plus de détails de ces développement peuvent être vus dans le cours de Mécanique Céleste de Luc Duriez.
Les polynômes de Legendre ont de nombreuses propriétés. Celle que nous allons utiliser dans l'exercice qui suit est la formule de Rodrigues:
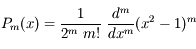
Cette formule va nous permettre de montrer que l'équation 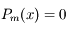 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_poly/equations_poly/equation55.png) et en a
et en a 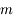 distinctes.
distinctes.
Auteur: Alain Vienne
 Les racines des polynômes de Legendre
Les racines des polynômes de Legendre
Difficulté : ☆☆
Temps : 1h (pour une rédaction correcte)
Les polynômes de Legendre, bien connus en Mécanique Céleste, peuvent se déterminer par la formule de Rodrigues:
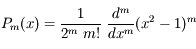
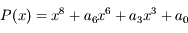
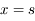 où
où 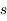 est la distance Terre-Soleil, et, on utilise cette racine pour factoriser le polynôme.
est la distance Terre-Soleil, et, on utilise cette racine pour factoriser le polynôme.


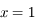 ua (
ua (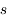 ) et les 2 autres racines dont celle à 5 ua.
) et les 2 autres racines dont celle à 5 ua.
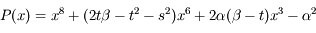
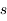 est la distance Terre-Soleil et
est la distance Terre-Soleil et 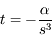 .
.
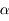 et
et 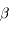 sont des coefficients réels issus de la géométrie du problème.
sont des coefficients réels issus de la géométrie du problème.
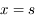 est racine de
est racine de 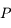 .
.
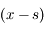 dans
dans 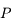 .
.
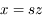 pour éliminer les fractions.
pour éliminer les fractions.
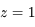 (ou équivalemment
(ou équivalemment 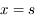 de la question précédente), repérer les groupes de termes qui s'annulent afin de mettre
de la question précédente), repérer les groupes de termes qui s'annulent afin de mettre 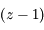 en facteur dans chacun de ces groupes
en facteur dans chacun de ces groupes
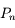 .
.
![U(r,\varphi)=\frac{KM_T}{r} \ [1 - \sum_{m=1}^{\infty} J_{2m} (\frac{a_e}{r})^{2m} P_{2m}(\sin\varphi) \ ]](../pages_poly/equations_poly/equation23.png)
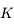 est la constante de gravitation de la Terre,
est la constante de gravitation de la Terre, 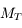 la masse totale de la Terre,
la masse totale de la Terre, 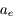 son rayon équatorial et
son rayon équatorial et 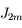 des coefficients numériques.
des coefficients numériques. 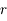 et
et 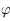 sont le rayon et la latitude du point pour lequel on évalue le potentiel
sont le rayon et la latitude du point pour lequel on évalue le potentiel 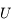 .
.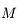 et
et 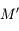 décrivant autour d'un centre
décrivant autour d'un centre 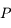 des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre
des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre 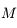 et
et 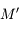 , on doit écrire l'inverse de la dsitance entre
, on doit écrire l'inverse de la dsitance entre 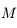 et
et 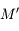 ,
, 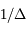 , en fonction de leurs éléments d'orbite. On montre facilement que:
, en fonction de leurs éléments d'orbite. On montre facilement que:
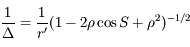
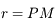 ,
, 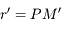 ,
, 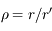 et
et 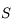 l'angle entre
l'angle entre 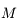 et
et 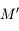 vu de
vu de 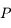 .
.
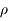 grâce aux polynômes de Legendre:
grâce aux polynômes de Legendre:
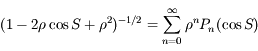
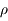 est petit. C'est le cas si, par exemple,
est petit. C'est le cas si, par exemple, 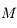 est la Terre,
est la Terre, 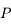 le Soleil et
le Soleil et 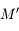 un satellite artificiel.
un satellite artificiel.
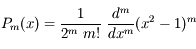
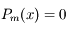 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_poly/equations_poly/equation55.png) et en a
et en a 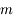 distinctes.
distinctes.
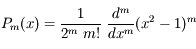
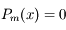 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_poly/equations_poly/equation59.png) et en a
et en a 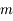 distinctes.
distinctes.
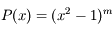 a
a 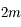 racines. Elles sont non disctinctes car il s'agit de
racines. Elles sont non disctinctes car il s'agit de 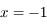 et
et 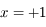 chacune d'elles étant d'ordre
chacune d'elles étant d'ordre 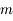 .
.
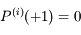 et
et 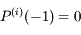 pour tout
pour tout 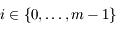 , où
, où
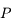 sur l'intervalle
sur l'intervalle ![[-1,+1]](../pages_poly/equations_poly/equation70.png)
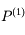 qui s'annulle en
qui s'annulle en 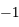 ,
, 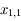 et
et 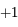 (ces trois racines sont distinctes)
(ces trois racines sont distinctes)
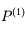 sur l'intervalle
sur l'intervalle ![[-1,x_{1,1}]](../pages_poly/equations_poly/equation76.png) , puis sur
, puis sur ![[x_{1,1},+1]](../pages_poly/equations_poly/equation77.png) . On a donc les racines
. On a donc les racines 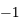 ,
, 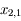 ,
, 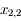 et
et 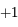 (ces quatres racines sont distinctes). Rédigez ensuite la récurrence. Une rédaction propre n'est pas si aisée. Faites la avec soin et choissisez bien vos notations (par exemple, bien différencier l'indice du polynôme et l'indice de la récurrence).
(ces quatres racines sont distinctes). Rédigez ensuite la récurrence. Une rédaction propre n'est pas si aisée. Faites la avec soin et choissisez bien vos notations (par exemple, bien différencier l'indice du polynôme et l'indice de la récurrence).
![(z-1)\ \ [s^8 z^6 (z+1) - 2 \alpha \beta s^3 z^3 (z^2+z+1) - \alpha^2 (z-1) (z^2+z+1)^2]](../pages_poly/equations_poly/equation19.png)
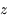 par
par 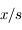 .
.