Les racines du polynôme de la méthode de Laplace

Auteurs: Alain Vienne, Marc Fouchard

Auteur: Alain Vienne

Lors de la découverte d'un nouvel objet dans le système solaire, on souhaite rapidement connaitre sa trajectoire. Celle-ci est généralement héliocentrique et, dans un premier temps, on la suppose képlérienne. Or les observations terrestres donnent uniquement la direction de l'astre mais pas sa distance. La méthode de Laplace propose un moyen qui, à partir de 3 observations de direction faites à des dates assez rapprochées, donne les vecteurs position et la vitesse de l'astre. Le détail de la méthode peut être trouvé dans le cours suivant: Dynamique du système solaire. On peut y voir notamment que la méthode conduit à chercher les racines d'un polynôme de degré 8. Il y est affirmé qu'il y a 4 racines réelles (1 négative, 3 positives) et 4 complexes non réelles. C'est cette affirmation qui est étudiée dans l'exercice qui suit.

Le polynôme est de la forme:

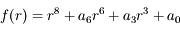
f(r)=r^8 + a_6 r^6 + a_3 r^3 + a_0

On sait que 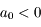a_0 < 0 et qu'il existe au moins 2 solutions distinctes strictement positives. L'une des deux est 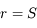r=S où 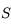est la distance Terre-Soleil. On peut aller voir l'exercice qui vérifie cette racine ici. La deuxième solution distincte de 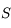et strictement positive suppose que les 3 observations ont été bien faites et correspondent physiquement à un même objet du système solaire. Elle n'est pas garantie mathématiquement mais s'appuie sur l'argument que cette solution "doit exister".

Voici à titre d'exemple le graphe du polynôme dans le cas de 3 observations de Jupiter à son opposition (courbe "complète" et un agrandissement):

Le polynome de la méthode de Laplace dans le cas de 3 observations de Jupiter (courbe "complète" et un agrandissement). L'axe horizontal est gradué en ua. On note que ce polynôme n'est pas très bien conditionné car la vue d'ensemble ne donne pas une idée des racines ni même du nombre de ces racines. La deuxième figure est agrandissement sur la partie utile. On voit la racine r=1

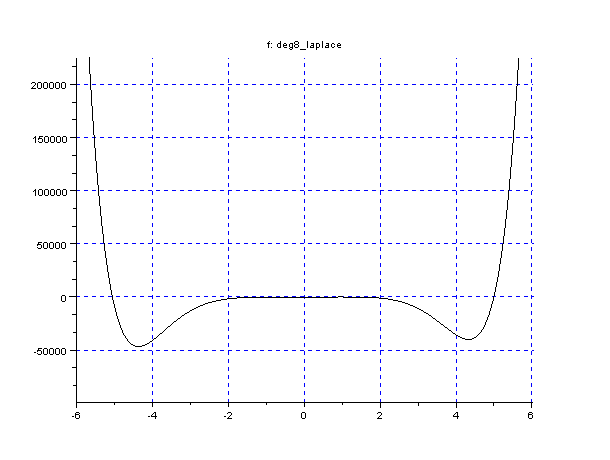
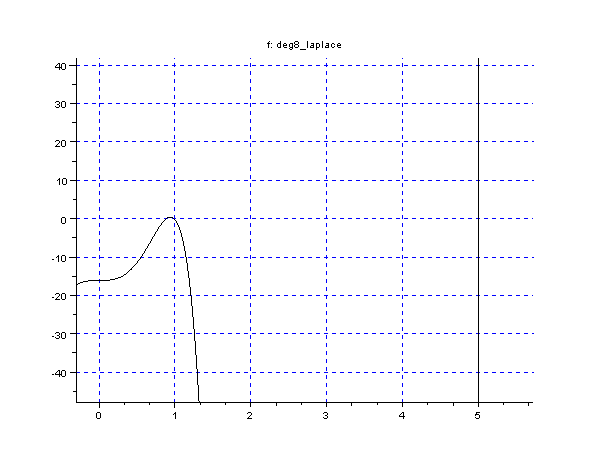
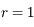ua (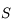

) et les 2 autres racines dont celle qui nous intéresse à 5 ua.

Crédit : Astrophysique sur Mesure / Vienne