Auteur: Alain Vienne

 Les racines du polynôme de la méthode de Laplace
Les racines du polynôme de la méthode de Laplace
Difficulté : ☆☆
Temps : 1h
Soit un polynôme à coefficients réels de la forme:
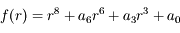
On sait que 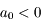 et qu'il existe au moins 2 solutions distinctes strictement positives.
et qu'il existe au moins 2 solutions distinctes strictement positives.
Question 1)
Calculer 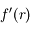 et étudier le polynôme
et étudier le polynôme 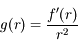 dans le cas où
dans le cas où 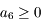
Question 2)
En déduire que 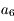 est strictement négatif
est strictement négatif
AideSolution
Voir que, dans ce cas, 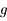 est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
Question 3)
Montrer que 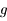 s'annule en un point
s'annule en un point 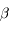 positif
positif
AideSolution
Utiliser le théorème de Rolle pour 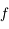 sur l'intervalle définie par ses 2 racines positives
sur l'intervalle définie par ses 2 racines positives
Question 5)
Monter que 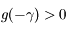 .
.
Aide
Question 7)
Etudier les 2 cas 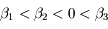 et
et 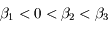 . Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
. Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
Aide
Dresser le tableau de variation de 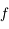 dans ces 2 cas.
dans ces 2 cas.
Question 8)
Conclure.
Solution
Comme on a supposé qu'il y avait au moins 2 racines positives, il y en a exactement 3. La question précédente avait montré une racine négative. Il y a donc exactement 4 racines réelles.
Or si on considère le polynôme 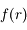 dans
dans ![\mathbb{C} [X]](../pages_af/equations_af/equation48.png) , le polynôme a 8 racines complexes. On en déduit que
, le polynôme a 8 racines complexes. On en déduit que 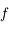 admet aussi 4 racines complexes non réelles.
admet aussi 4 racines complexes non réelles.


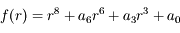
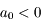 et qu'il existe au moins 2 solutions distinctes strictement positives.
et qu'il existe au moins 2 solutions distinctes strictement positives.
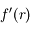 et étudier le polynôme
et étudier le polynôme 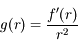 dans le cas où
dans le cas où 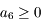
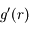 peut donc s'écrire
peut donc s'écrire 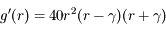 (avec
(avec 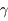 positif). Monter que
positif). Monter que 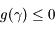 .
.
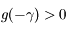 .
.
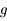 s'annule en
s'annule en 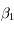 ,
, 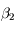 et
et 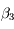 tels que
tels que 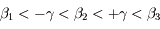
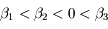 et
et 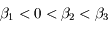 . Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
. Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives