

Ex : projection de Mollweide |
Difficulté : ☆☆ Temps : 1h30
Nous allons commencer par étudier la fonction:
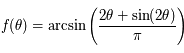 ,
,
sur l'intervalle ![I=[-\pi/2,\pi/2]](../pages_af/equations_af/equation124.png) .
.
Montrer que 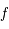 est définie et continue sur
est définie et continue sur 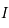 et qu'elle est impaire.
et qu'elle est impaire.
En déduire que 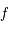 est strictement croissante de
est strictement croissante de 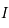 dans lui-même et donc qu'il existe une fonction réciproque, notée
dans lui-même et donc qu'il existe une fonction réciproque, notée 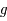 .
Déterminer les propriétés principales de
.
Déterminer les propriétés principales de 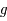 et en particulier que
et en particulier que ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation157.png)
On remarque que pour 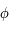 donné,
donné, 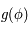 est la solution de l'équation (*).
est la solution de l'équation (*).
En déduire l'image des points, ou des ensembles de points suivants, par la projection de Mollweide :
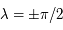 .
.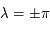 .
.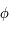 .
.
La fonction 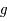 n'est pas définie analytiquement. On va montrer ici qu'on peut estimer
n'est pas définie analytiquement. On va montrer ici qu'on peut estimer 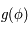 par la méthode de Newton-Raphson.
Soit
par la méthode de Newton-Raphson.
Soit 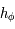 la fonction définie sur
la fonction définie sur ![[-\pi/2,\pi/2]](../pages_af/equations_af/equation219.png) par :
par :
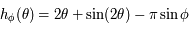 .
.
Résoudre l'équation (*) revient donc à résoudre 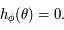
Montrer que si 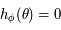 alors
alors 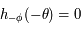 et que si
et que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation224.png) alors la solution de
alors la solution de 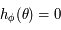 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation226.png) .
De même montrer que
.
De même montrer que 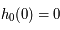 et
et 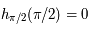 .
.
Ainsi on peut se limiter à résoudre 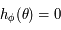 pour
pour ![\phi\in]0,\pi/2[](../pages_af/equations_af/equation239.png) . On sait déjà que la solution se trouve dans
. On sait déjà que la solution se trouve dans ![]0,\pi/2[](../pages_af/equations_af/equation240.png) d'après la question 3.
Montrer que, pour
d'après la question 3.
Montrer que, pour ![\phi\in]0,\pi/2[](../pages_af/equations_af/equation241.png) ,
, 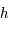 est définie continue dérivable et strictement croissante sur
est définie continue dérivable et strictement croissante sur 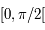 et que sa dérivée est définie continue, strictement positive et strictement décroissante sur
et que sa dérivée est définie continue, strictement positive et strictement décroissante sur 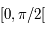 .
.
Soit 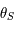 la solution de
la solution de 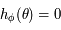 . Soit
. Soit 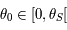 . On note
. On note 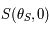 et
et 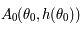 les points de la courbe représentative
les points de la courbe représentative 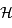 de
de 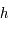 dans un repère orthonormé.
On note
dans un repère orthonormé.
On note 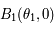 , le point d'intersection de la tangente en
, le point d'intersection de la tangente en 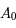 à
à 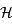 avec l'axe des abscisses.
Montrer que
avec l'axe des abscisses.
Montrer que 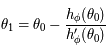 et que
et que 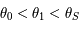 .
.
Montrer que la suite définie par 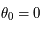 et
et 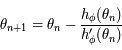 converge vers
converge vers 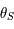 .
.
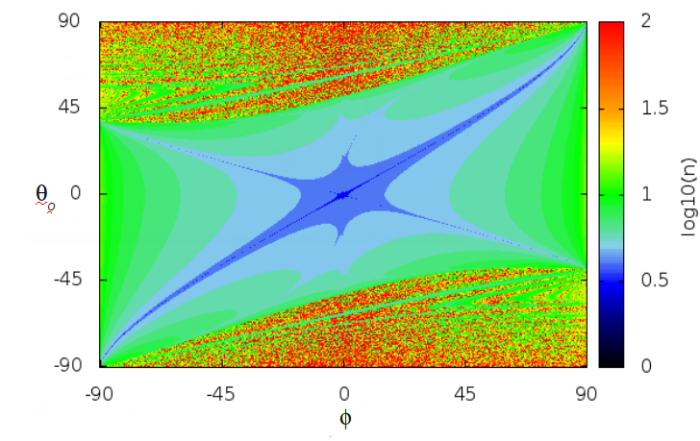
La convergence de cette suite dépend fortement du choix de 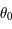 . La figure ci-dessous montre le nombre d'itérations nécessaires pour attendre un précision relative de l'ordre de
. La figure ci-dessous montre le nombre d'itérations nécessaires pour attendre un précision relative de l'ordre de 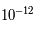 sur
sur 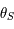 en fonction de
en fonction de 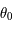 et
et 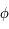 .
On voit que pour certains choix la convergence est très mauvaise voire impossible. Par contre avec
.
On voit que pour certains choix la convergence est très mauvaise voire impossible. Par contre avec 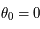 , la méthode converge pour toute valeur de
, la méthode converge pour toute valeur de 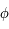 même si ce n'est pas le choix optimal.
même si ce n'est pas le choix optimal.
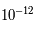 sur
sur 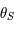 en fonction de
en fonction de 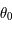 et
et 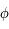 .
.