Loi de Wien

Auteurs: Marc Fouchard, Jérôme Thiébaut

Auteur : Marc Fouchard

La loi de Planck indique que pour un corps noir, l'énergie émise par rayonnement à une longueur d'onde donnée, ne dépend que de la température de surface du corps noir. Cette loi est donnée par la relation suivante :

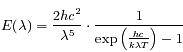
$E(\lambda)=\frac{2 h c^2}{\lambda ^5}\cdot \frac{1}{\exp \left( \frac{h c}{k \lambda T} \right) -1}$

où 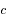correspond à la vitesse de la lumière dans le vide, 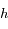est la constante de Planck, 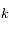la constante de Boltzmann, 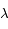$\lambda$ la longueur d'onde à laquelle le rayonnement est émis et 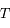la température de surface du corps noir.

La figure ci dessous montre le comportement de 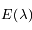$E(\lambda)$ pour différentes températures de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.

Crédit : Astrophysique sur Mesure

Le but de cet exercice est de trouver la relation exacte entre 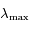$\lambda_{\rm max}$ et .

Remarque

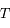Cette exercice repose sur la détermation du maximum d'une fonction sur un intervalle donné. Il utilise aussi le théorème du point fixe dans 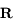$\mathbf R$ , mais ce théorème peut être admis ici.