

Ex: Etoile à neutron |
Difficulté : ☆ Temps : 45 min
On assimile l'étoile à neutron à un gaz parfait de neutrons contenu dans une sphère. La densité d'états (ou fonction de distribution) de l'impulsion 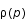 est la suivante:
est la suivante: 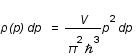 , où V est le volume et
, où V est le volume et 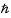 la constante de Planck réduite.
la constante de Planck réduite.
On définit la densité de particule n:
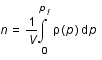 où
où 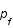 est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de
est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de 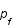 .
.
Exprimer l'impulsion de Fermi en fonction de la masse du neutron, m, celle de l'étoile, M, et du rayon de l'étoile, R.
On définit la densité d'énergie, 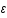 :
:
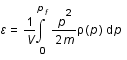 .
calculer
.
calculer 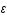 en fonction de
en fonction de 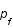 .
.
L'énergie du gaz E vallant 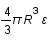 , l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
, l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
L'énergie gravitationnelle de l'étoile est 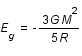 , où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon
, où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon 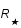 qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et
qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et 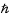 . Calculer ce rayon pour le soleil.
. Calculer ce rayon pour le soleil.