Ex: Sphère photonique

Auteurs: Marc Fouchard, Jérôme Thiébaut

Auteur: Jérôme Thiébaut

Sphère photonique

Difficulté : ☆ Temps : 20mn

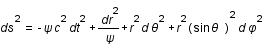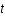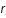
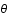
La métrique de Schwarzschild est une métrique applicable à un corps massif central statique ou en rotation lente. Elle s'écrit: ds^2=-psi*c^2*dt^2+dr^2/psi+r^2*d*theta^2+r^2*sin(theta)^2*d*phi^2 , où est le temps,c la vitesse de la lumière, 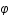theta phi sont les coordonnées sphériques et 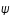psi est défini comme 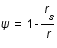psi=1-r_s/r . Le rayon de Schwarzschild 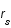r_s est directement relié à la masse du corps central par 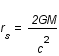r_s=2GM/c^2 , où G est la constante de gravitation.

Question 1)

On se place dans le plan 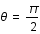theta=pi/2 . Que vaut 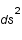ds^2 dans le cas d'une orbite circulaire ?

Solution

Question 2)

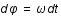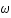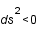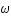On pose d*phi=omega*dt , où omega est la fréquence angulaire du mouvement vu par un observateur lointain. Sachant que pour qu'un mouvement soit physiquement réalisable il faut que ds^2<0 (ceci vient uniquement d'un choix spécifique de métrique); déterminer la condition sur omega .

Aide Solution

Question 3)

Montrer que l'orbite finale (correspondant à la fréquence limite calculée précédemment) correspond à la trajectoire de photons pour lesquels 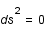ds^2=0 . Que vaut son rayon ?

Solution