

Projection de Mollweide |
Auteur: Marc Fouchard
La projection de Mollweide est la projection d'une sphère sur un plan qui conserve les aires au sacrifice de la conservation des distances et des formes. La projection d'une sphère rempli une ellipse dont le petit axe est le double du grand axe.
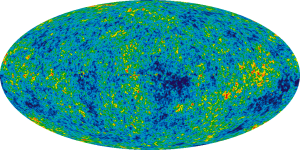
L'avantage d'une telle projection en astronomie est qu'elle permet d'avoir une idée globale de la répartition d'une certaine quantité sur la sphère céleste par unité de surface (ou stéradian). Par exemple, l'image suivante montre la répartition du rayonnement du fond cosmologique sur une projection de Mollweide de la sphère céleste. Comme ce rayonnement est mesuré par unité de surface (ou par stéradian), la conservation des aires est ici fondamentale pour bien visualiser les données.
Sur une sphère, on défini un système de coordonnées en choisissant un plan de référence (par exemple l'équateur), à partir duquel seront
mesurées les latitudes, notées 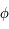 , un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées
, un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées 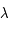 .
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
.
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
Les coordonnées 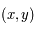 par la projection de Mollweide d'un point de coordonnées
par la projection de Mollweide d'un point de coordonnées 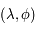 de la sphère céleste sont définies par:
de la sphère céleste sont définies par:
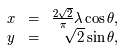
où la longitude 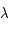 est mesurée entre
est mesurée entre 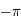 et
et 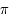 et
et 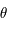 est un angle auxiliaire défini par :
est un angle auxiliaire défini par :
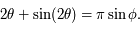 (*)
(*)
L'équation (*) ne peut être résolue analytiquement. Le but de cet exercice est de trouver une méthode permettant de déterminer 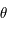 afin de pouvoir calculer
afin de pouvoir calculer 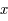 et
et 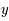 .
.