images/logos_obspm_lille1.png

L'Astronomie dans l'apprentissage des Mathématiques

L'Astronomie dans l'apprentissage des Mathématiques

Fonction d'une variable réelle : dérivabilité

Théorème des accroissements finis

• Les racines du polynôme de la méthode de Laplace

• Ex: Les racines du polynôme de la méthode de Laplace

• Les racines des polynômes de Legendre

• Ex: Les racines des polynômes de Legendre

• Projection de Mollweide

• Ex : projection de Mollweide

Les racines des polynômes de Legendre

Auteurs: Alain Vienne, Marc Fouchard

Auteur: Alain Vienne

En Mécanique Céleste, on est souvent conduit à utiliser les polynômes de Legendre que l'on note ici 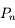P_n .

C'est le cas, par exemple, dans le développement du potentiel terrestre. Si on suppose que la Terre est un sphéroïde, le potentiel peut s'écrire:

$U(r,\varphi)=\frac{KM_T}{r} \ [1 - \sum_{m=1}^{\infty} J_{2m} (\frac{a_e}{r})^{2m} P_{2m}(\sin\varphi) \ ]$

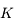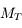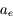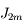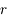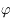est la constante de gravitation de la Terre, M_T la masse totale de la Terre, a_e son rayon équatorial et $J_{2m}$ des coefficients numériques. et $\varphi$ sont le rayon et la latitude du point pour lequel on évalue le potentiel .

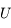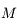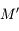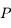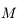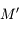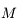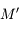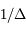Un autre exemple d'utilisation est de considérer 2 corps et décrivant autour d'un centre des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre et , on doit écrire l'inverse de la dsitance entre et , $1/\Delta$ , en fonction de leurs éléments d'orbite. On montre facilement que:

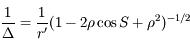
$\frac{1}{\Delta} = \frac{1}{r'} (1-2\rho \cos S + \rho^2)^{-1/2}$

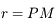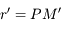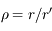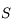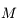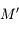Avec r=PM , r'=PM' , $\rho = r/r'$ et l'angle entre et vu de .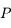

Cette dernière expression est développée en puissance de 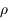$\rho$ grâce aux polynômes de Legendre:

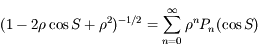
$(1-2\rho \cos S + \rho^2)^{-1/2} = \sum_{n=0}^{\infty} \rho^n P_n(\cos S)$

Ce développement est rapidement convergent si 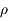$\rho$ est petit. C'est le cas si, par exemple, 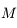est la Terre, 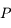le Soleil et 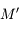un satellite artificiel.

Plus de détails de ces développement peuvent être vus dans le cours de Mécanique Céleste de Luc Duriez.

Les polynômes de Legendre ont de nombreuses propriétés. Celle que nous allons utiliser dans l'exercice qui suit est la formule de Rodrigues:

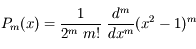
$P_m(x)=\frac{1}{2^m \ m!} \ \frac{d^m}{dx^m} (x^2-1)^m$

Cette formule va nous permettre de montrer que l'équation 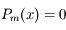P_m(x)=0 a toutes ses racines dans [-1,+1] et en a 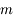distinctes.