De nombreux processus physiques correspondent à une situation où l'on compte des événements aléatoires indépendants. C'est par exemple le cas des désintégrations radioactives ou de l'émission de lumière par une source, de façon générale toute situation où l'événement se produit avec une probabilité constante par unité de temps. On veut connaître précisément la loi du phénomène pour calculer les fluctuations associées et les minimiser.
La loi de Poisson est ainsi utilisée pour rendre compte de phénomènes aléatoires qui vérifient les deux propriétés suivantes :
- Les occurrences du phénomène sont indépendantes.
- La probabilité d'apparition du phénomène dans un intervalle de temps ne dépend que de la durée
 de cet intervalle.
de cet intervalle.
Un événement se produisant en moyenne avec une fréquence 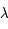 , on note P(k) la densité de probabilité pour qu'il se produise k fois durant le temps t (avec k ≥ 0). La loi de Poisson de paramètre
, on note P(k) la densité de probabilité pour qu'il se produise k fois durant le temps t (avec k ≥ 0). La loi de Poisson de paramètre 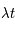 donne :
donne :
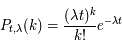
où k! est la factorielle.
L'appliquette ci-dessous illustre la loi de Poisson : elle trace les valeurs obtenues au cours d'un certain nombre de tirages, pour une valeur de 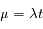 donnée.
donnée.
Loi de Poisson 
 Dérivation de la loi de Poisson
Dérivation de la loi de Poisson
Difficulté : ☆☆
Temps : 40 min
Question 1)
Retrouver la forme générale de la loi de Poisson à partir d'un raisonnement discret.
On découpe la durée considérée en n petits intervalles de temps, et on utilise une loi binomiale.
Question 2)
Déterminer la moyenne et l'écart-type de la loi de Poisson.
Question 3)
On observe une source lumineuse faible pendant un temps  . Quel est le nombre de photons détectés en moyenne, de quoi dépend-il ? Que représente l'écart-type de cette distribution ? Quel paramètre permet de quantifier la précision de la mesure, et comment améliorer la mesure de cette source ?
. Quel est le nombre de photons détectés en moyenne, de quoi dépend-il ? Que représente l'écart-type de cette distribution ? Quel paramètre permet de quantifier la précision de la mesure, et comment améliorer la mesure de cette source ?
 Remarque
Remarque
L'applet ci-dessous illustre ce dernier résultat : on améliore le rapport signal sur bruit en posant plus longtemps, mais cette amélioration est lente.
Elle est spectaculaire au début (en permettant la reconnaissance de l'objet), mais ralentit de plus en plus (les détails sont de plus en plus longs à se préciser).
Loi de Poisson 
La loi de distribution gaussienne est sans doute la plus employée, en physique comme ailleurs, à tel point qu'on l'appelle généralement loi normale.
La densité de probabilité gaussienne est :
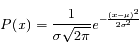
Dans cette formulation, 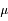 représente la moyenne, et
représente la moyenne, et 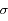 l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
On remarque la symétrie de la fonction autour du pic central, et son aspect caractéristique ("en cloche"). On note habituellement N(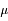 ,
, 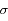 ) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).
) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).
L'importance de la loi normale est liée au théorème de la limite centrale, qui montre que la superposition de lois de distribution différentes tend vers une loi normale. Ceci est en particulier important pour estimer les erreurs de mesure : si elles sont de provenance différentes, et de statistique mal connue, on peut généralement faire l'approximation que leur somme est distribuée de manière gaussienne. C'est le théorème de la limite centrale qui explique l'omniprésence de la loi normale.
gaussiennes
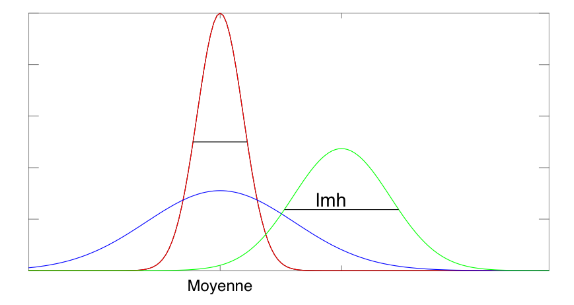
Exemples de gaussiennes de moyenne et largeur à mi-hauteur variables. La surface sous la courbe est normalisée à 1.
 Limite de détection d'un objet ponctuel
Limite de détection d'un objet ponctuel
Difficulté : ☆
Temps : 20 min
 Remarque
Remarque
Le calcul des moments de la loi normale est donné ici en exercice.
Question 1)
Calculer la largeur à mi-hauteur de la gaussienne
Question 2)
Déterminer graphiquement l'aire délimitée par une gaussienne entre ± 1, 2 et 3 écart-types de la valeur moyenne. Quel est l'intérêt de cette question ?
Question 3)
On observe un astéroïde de la ceinture principale avec un télescope de 2 m depuis le sol. Le fond de ciel produit un signal de 100 pas-codeurs à la sortie de la caméra. A quel niveau de signal peut-on penser avoir détecté l'objet ?
Un télescope de cette taille n'est pas normalement équipé d'un dispositif d'optique adaptative. La résolution angulaire est donc limitée par la turbulence atmosphérique, et à cette distance l'objet apparaît quasiment ponctuel.
Le signal total en provenance de l'objet est donc concentré sur quelques pixels (la taille de la tache de diffraction). Il est à comparer avec le niveau du ciel et ses fluctuations.
On se propose d'estimer le temps nécessaire pour qu'un photon produit dans le Soleil soit émis à sa surface.
Le processus correspond à une suite d'émissions et absorptions successives par les atomes rencontrés en chemin. On l'assimile à une marche au hasard en trois dimensions (bien que l'identité du photon ne soit pas conservée au cours de ces événements, et que la longueur d'onde puisse changer au cours des diffusions successives).
Auteur: Stéphane Erard
 Chemin optique d'un photon dans le Soleil
Chemin optique d'un photon dans le Soleil
Difficulté : ☆
Temps : 45 min
Question 1)
On considère une particule se déplaçant en trois dimensions de façon aléatoire par pas de longueur d. Ecrire sa position en coordonnées sphériques après le premier pas. La distance d est appelée libre parcours moyen.
Question 2)
Ecrire les coordonnées après N pas en fonction des directions successives. Quelle est la distance au point de départ ?
Question 3)
Simplifier cette expression, sachant que les directions successives sont aléatoires et indépendantes.
Question 4)
On donne la densité 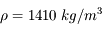 et le coefficient d'absorption massique
et le coefficient d'absorption massique 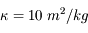 , qu'on suppose uniformes au premier ordre. Calculer le libre parcours moyen.
, qu'on suppose uniformes au premier ordre. Calculer le libre parcours moyen.
Question 5)
Connaissant le rayon du Soleil 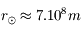 , combien de diffusions un photon produit au centre du Soleil subit-il en moyenne avant d'arriver en surface ? Quelle est la longueur du trajet réellement parcouru dans le Soleil ? Combien de temps faut-il au photon pour effectuer le trajet ?
, combien de diffusions un photon produit au centre du Soleil subit-il en moyenne avant d'arriver en surface ? Quelle est la longueur du trajet réellement parcouru dans le Soleil ? Combien de temps faut-il au photon pour effectuer le trajet ?
-
Question 1
Aide :
On découpe la durée considérée en n petits intervalles de temps, et on utilise une loi binomiale.
Solution :
Le problème est équivalent à calculer la probabilité de trouver k occurrences de l'événement pour n tirages, la probabilité de réalisation durant chaque intervalle étant p = λt/n.
La loi de Bernoulli donne :
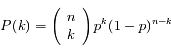
Où 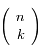 est le nombre de combinaisons de k éléments parmi n (notation standard moderne).
est le nombre de combinaisons de k éléments parmi n (notation standard moderne).
Pour passer à la limite continue, on prend n → ∞ en gardant pn = λt, et on remarque que :
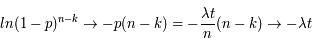
Par ailleurs,
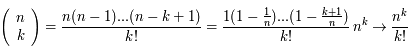
Au total on trouve bien l'expression de la loi de Poisson :
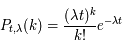
-
Question 2
Solution :
Si X est une variable aléatoire discrète suivant une loi de Poisson, sa valeur moyenne s'écrit :
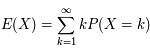
On note ici 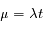
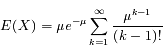
On remarque que la série est le développement de l'exponentielle, il reste :
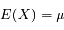
La variance de X s'écrit :
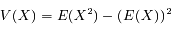
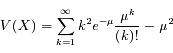
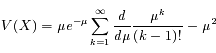
![V(X) = \mu e^{-\mu} \frac{d}{d\mu}[\mu e^{\mu}] - \mu^2](../pages_proba/equations_proba/equation18.png)
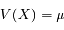
D'où l'écart-type : 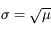
-
Question 3
Solution :
Si la fréquence d'émission des photons par la source est λ, le nombre moyen de photons détectés (valeur moyenne du signal) est :
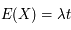
Cette quantité est proportionnelle au temps de pose  et à la fréquence d'émission.
et à la fréquence d'émission.
L'écart-type 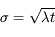 réprésente la variation moyenne autour de cette valeur moyenne, qu'on observerait par exemple entre des mesures successives. Cette fluctuation est liée au processus d'émission de photons lui-même, pas à la méthode de mesure ; c'est donc une incertitude fondamentale qu'on ne peut pas outrepasser en changeant d'instrument. On l'appelle couramment bruit de photons dans ce cas.
réprésente la variation moyenne autour de cette valeur moyenne, qu'on observerait par exemple entre des mesures successives. Cette fluctuation est liée au processus d'émission de photons lui-même, pas à la méthode de mesure ; c'est donc une incertitude fondamentale qu'on ne peut pas outrepasser en changeant d'instrument. On l'appelle couramment bruit de photons dans ce cas.
La qualité de la mesure est estimée par le rapport signal sur bruit. Si aucune autre incertitude n'affecte cette mesure, le rapport signal sur bruit est :
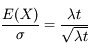
On améliore donc la mesure en posant plus longtemps, mais cette amélioration est lente (en racine de t, voir l'animation ci-dessous).
-
Question 1
Solution :
La largeur à mi-hauteur (FWHM) correspond à la valeur de la variable pour laquelle la fonction est réduite de moitié par rapport au pic central, soit :
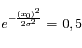
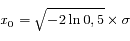
et 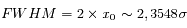
-
Question 2
Solution :
Une intégration numérique donne :
Table 1
| X |
Pr(X) |
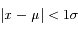
|
0,68 |
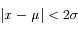
|
0,955 |
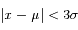
|
0,997 |
Probabilités gaussiennes
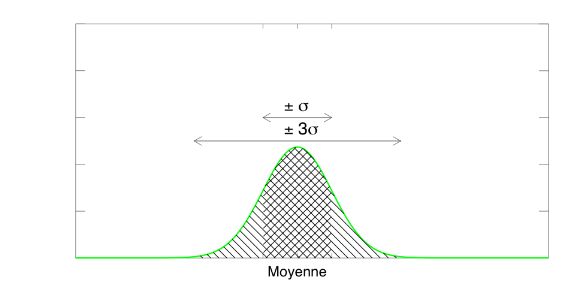
La totalité des observations (à 3 ‰ près) se répartit à moins de 3 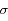 de la moyenne. C'est la limite de détection généralement utilisée pour des mesures.
de la moyenne. C'est la limite de détection généralement utilisée pour des mesures.
-
Question 3
Aide :
Un télescope de cette taille n'est pas normalement équipé d'un dispositif d'optique adaptative. La résolution angulaire est donc limitée par la turbulence atmosphérique, et à cette distance l'objet apparaît quasiment ponctuel.
Le signal total en provenance de l'objet est donc concentré sur quelques pixels (la taille de la tache de diffraction). Il est à comparer avec le niveau du ciel et ses fluctuations.
Solution :
Le niveau du fond de ciel suit une loi de Poisson. Les fluctuations associées sont donc en racine de N, soit un écart-type de 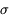 =10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3
=10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3 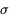 = 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
= 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
Cependant, on a dans ce cas de très nombreux pixels (on utilise typiquement des détecteurs de 500x500), et donc un nombre significatif de pixels à 3 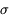 (750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.
(750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.
Détection à 5 sigma, LMH = 1.5 pixels

Image 512x512 avec un fond poissonien à 100 pas-codeurs. Selon le critère usuel, on a ici une détection extrêmement bonne : à 5
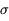
, étendue sur une dizaine de pixels voisins. Saurez-vous trouver l'astéroïde ?
Détection 5 sigma, lmh = 2 pixels

Dans le cas où la tache de diffaction est légèrement plus grande, l'identification visuelle devient relativement aisée.
Remarque : attention, dans les deux exemples ci-dessus le niveau de la source (l'intégrale du signal sur tous les pixels de la tâche de diffraction) est différent. Dans le deuxième exemple, la source est plus étalée mais en fait beaucoup plus brillante (le niveau maximum est identique malgré l'étalement du signal). Si on dégrade la résolution en sommant sur des boîtes larges de quelque lmh, on revient à une situation où l'on peut comparer l'écart avec la loi normale ; mais on voit que le critère à 3 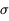 est généralement insuffisant pour ce type d'application.
est généralement insuffisant pour ce type d'application.
-
Question 1
Solution :
Après un pas de longueur d, on a :
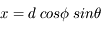
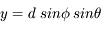
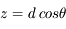
-
Question 2
Solution :
Après N pas de longueur d, l'expression générique des coordonnées est :
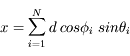
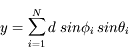
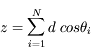
La distance au point de départ est :
![r^2 = x^2+ y^2 + z^2 = d^2 \biggl[(\sum_{i=1}^{N}cos \phi_{i} \; sin \theta_{i})^2+ (\sum_{i=1}^{N}sin \phi_{i} \; sin \theta_{i})^2 + (\sum_{i=1}^{N} \; cos \theta_{i})^2) \biggl]](../pages_proba/equations_proba/equation50.png)
-
Question 3
Solution :
Si on développe le premier terme, on voit que :
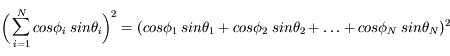
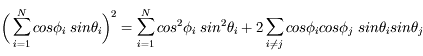
Les directions 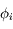 et
et 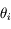 étant aléatoires et indépendantes, le second terme s'annule en moyenne. On a donc :
étant aléatoires et indépendantes, le second terme s'annule en moyenne. On a donc :
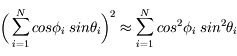
Les deux autres termes intervenant dans la distance donnent de façon similaire :
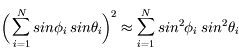
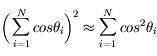
Si N est suffisamment grand, on a donc :
![r^2 = d^2 \biggl[\sum_{i=1}^{N}cos^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N}sin^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N} \; cos^2 \theta_{i}) \biggl]](../pages_proba/equations_proba/equation58.png) soit
soit
![r^2 = d^2 \sum_{i=1}^{N}[(cos^2 \phi_{i}+sin^2 \phi_{i}) \; sin^2 \theta_{i} + \; cos^2 \theta_{i}]](../pages_proba/equations_proba/equation59.png) ou encore
ou encore
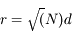
-
Question 4
Solution :
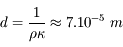
-
Question 5
Solution :
Le nombre de diffusions subi est 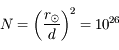
La distance parcourue dans le Soleil est 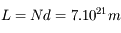 , soit
, soit 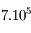 années-lumière.
années-lumière.
Le photon se déplace par définition à la vitesse de la lumière, 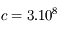 m/s. Le trajet prend donc un temps
m/s. Le trajet prend donc un temps 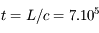 an, près d'un million d'années — à comparer aux 8 minutes requises pour pourcourir la distance Soleil-Terre dans le vide.
an, près d'un million d'années — à comparer aux 8 minutes requises pour pourcourir la distance Soleil-Terre dans le vide.
 de cet intervalle.
de cet intervalle.
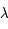 , on note P(k) la densité de probabilité pour qu'il se produise k fois durant le temps t (avec k ≥ 0). La loi de Poisson de paramètre
, on note P(k) la densité de probabilité pour qu'il se produise k fois durant le temps t (avec k ≥ 0). La loi de Poisson de paramètre 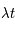 donne :
donne :
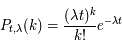
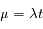 donnée.
donnée.

 . Quel est le nombre de photons détectés en moyenne, de quoi dépend-il ? Que représente l'écart-type de cette distribution ? Quel paramètre permet de quantifier la précision de la mesure, et comment améliorer la mesure de cette source ?
. Quel est le nombre de photons détectés en moyenne, de quoi dépend-il ? Que représente l'écart-type de cette distribution ? Quel paramètre permet de quantifier la précision de la mesure, et comment améliorer la mesure de cette source ?
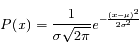
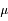 représente la moyenne, et
représente la moyenne, et 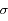 l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
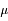 ,
, 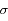 ) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).
) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).

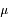 > 5).
> 5).
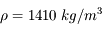 et le coefficient d'absorption massique
et le coefficient d'absorption massique 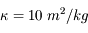 , qu'on suppose uniformes au premier ordre. Calculer le libre parcours moyen.
, qu'on suppose uniformes au premier ordre. Calculer le libre parcours moyen.
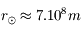 , combien de diffusions un photon produit au centre du Soleil subit-il en moyenne avant d'arriver en surface ? Quelle est la longueur du trajet réellement parcouru dans le Soleil ? Combien de temps faut-il au photon pour effectuer le trajet ?
, combien de diffusions un photon produit au centre du Soleil subit-il en moyenne avant d'arriver en surface ? Quelle est la longueur du trajet réellement parcouru dans le Soleil ? Combien de temps faut-il au photon pour effectuer le trajet ?
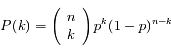
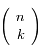 est le nombre de combinaisons de k éléments parmi n (notation standard moderne).
est le nombre de combinaisons de k éléments parmi n (notation standard moderne).
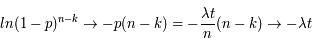
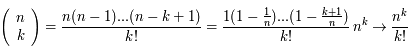
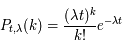
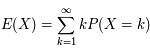
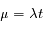
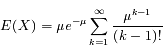
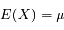
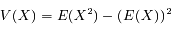
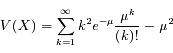
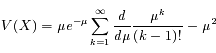
![V(X) = \mu e^{-\mu} \frac{d}{d\mu}[\mu e^{\mu}] - \mu^2](../pages_proba/equations_proba/equation18.png)
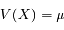
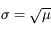
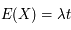
 et à la fréquence d'émission.
et à la fréquence d'émission.
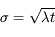 réprésente la variation moyenne autour de cette valeur moyenne, qu'on observerait par exemple entre des mesures successives. Cette fluctuation est liée au processus d'émission de photons lui-même, pas à la méthode de mesure ; c'est donc une incertitude fondamentale qu'on ne peut pas outrepasser en changeant d'instrument. On l'appelle couramment bruit de photons dans ce cas.
réprésente la variation moyenne autour de cette valeur moyenne, qu'on observerait par exemple entre des mesures successives. Cette fluctuation est liée au processus d'émission de photons lui-même, pas à la méthode de mesure ; c'est donc une incertitude fondamentale qu'on ne peut pas outrepasser en changeant d'instrument. On l'appelle couramment bruit de photons dans ce cas.
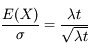
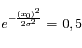
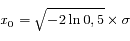
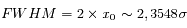
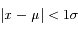
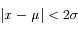
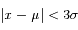

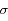 de la moyenne. C'est la limite de détection généralement utilisée pour des mesures.
de la moyenne. C'est la limite de détection généralement utilisée pour des mesures.
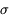 =10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3
=10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3 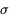 = 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
= 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
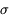 (750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.
(750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.

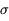 , étendue sur une dizaine de pixels voisins. Saurez-vous trouver l'astéroïde ?
, étendue sur une dizaine de pixels voisins. Saurez-vous trouver l'astéroïde ?

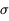 est généralement insuffisant pour ce type d'application.
est généralement insuffisant pour ce type d'application.
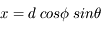
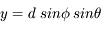
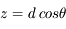
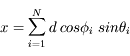
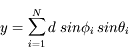
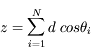
![r^2 = x^2+ y^2 + z^2 = d^2 \biggl[(\sum_{i=1}^{N}cos \phi_{i} \; sin \theta_{i})^2+ (\sum_{i=1}^{N}sin \phi_{i} \; sin \theta_{i})^2 + (\sum_{i=1}^{N} \; cos \theta_{i})^2) \biggl]](../pages_proba/equations_proba/equation50.png)
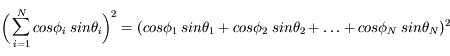
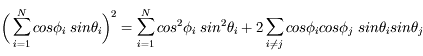
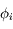 et
et 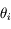 étant aléatoires et indépendantes, le second terme s'annule en moyenne. On a donc :
étant aléatoires et indépendantes, le second terme s'annule en moyenne. On a donc :
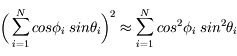
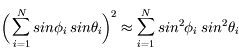
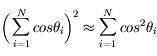
![r^2 = d^2 \biggl[\sum_{i=1}^{N}cos^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N}sin^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N} \; cos^2 \theta_{i}) \biggl]](../pages_proba/equations_proba/equation58.png) soit
soit
![r^2 = d^2 \sum_{i=1}^{N}[(cos^2 \phi_{i}+sin^2 \phi_{i}) \; sin^2 \theta_{i} + \; cos^2 \theta_{i}]](../pages_proba/equations_proba/equation59.png) ou encore
ou encore
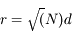
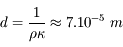
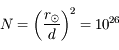
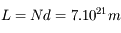 , soit
, soit 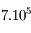 années-lumière.
années-lumière.
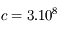 m/s. Le trajet prend donc un temps
m/s. Le trajet prend donc un temps 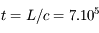 an, près d'un million d'années — à comparer aux 8 minutes requises pour pourcourir la distance Soleil-Terre dans le vide.
an, près d'un million d'années — à comparer aux 8 minutes requises pour pourcourir la distance Soleil-Terre dans le vide.