Auteur: Stéphane Erard

 Intégrales gaussiennes
Intégrales gaussiennes
Difficulté : ☆☆
Temps : 60 min
Le calcul des propriétés de la loi normale suppose l'intégration de la fonction gaussienne, et des intégrales similaires apparaissent dans le calcul suivant.
Le moment d'ordre n de la loi normale réduite (de moyenne nulle) est :
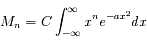
où a > 0 et n ≥ 0, C étant une constante de normalisation. On s'intéresse ici à :
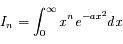
Question 1)
Trouver une relation de récurrence entre les intégrales 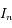 .
.
AideSolution
On intègre par partie en posant
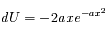
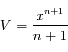
On trouve
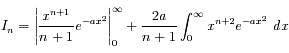
Soit
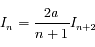
Question 2)
Calculer 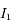 . Que représente cette quantité ?
. Que représente cette quantité ?
Solution
En posant 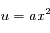 on trouve :
on trouve :
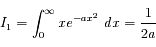
Cette quantité n'est pas proportionnelle à la moyenne de la loi normale centrée, qui est l'intégrale étendue à toute la droite réelle. Celle-ci est nulle, comme tous les moments d'ordre impair, ce qui dérive de la parité de la fonction.
Question 3)
Calculer l'intégrale de Gauss 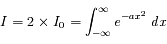
Solution
La méthode la plus simple est de calculer le carré de l'intégrale et de passer en coordonnées polaires. On trouve au final :
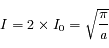
D'où le coefficient habituel de la loi normale qui normalise l'intégrale à 1.
Question 4)
En déduire les moments de la loi normale centrée.
Solution
La fonction étant paire, tous les moments d'ordre impair sont nuls. Les moments pairs suivent la relation de récurrence donnée plus haut à partir de 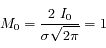 (normalisation de la densité de probabilité).
(normalisation de la densité de probabilité).
Auteur: Stéphane Erard

 Distribution des vitesses
Distribution des vitesses
Difficulté : ☆☆
Temps : 60 min
La probabilité pour qu'une molécule ait une vitesse comprise entre 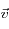 et
et 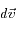 est notée
est notée 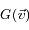 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
Question 1)
Ecrire les conditions d'indépendance entre les composantes du vecteur vitesse, et d'isotropie.
Solution
En posant 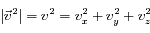
l'indépendance entre composantes de vitesse s'écrit :
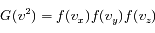
L'isotropie se traduit par :
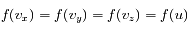 Soit :
Soit : 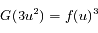
On peut donc écrire :
![G(v_x^2+v_y^2+v_z^2) = \left[G(3v_x^2) G(3v_y^2) G(3v_z^2)\right]^{1/3}](../pages_int-gen/equations_int-gen/equation66.png)
Question 2)
En déduire la forme de G.
Solution
On prend le logarithme et on pose 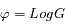 :
:
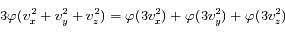
C'est la définition d'une fonction linéaire. On a donc :
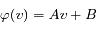
Soit
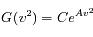
Question 3)
Identifier deux conditions qui permettent de calculer les coefficients ci-dessus.
Solution
G est une densité de probabilité, elle est donc normalisée :
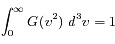
Par ailleurs on connaît la vitesse quadratique moyenne :
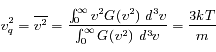
Question 4)
Calculer les intégrales 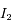 et
et 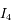 de l'exercice précédent.
de l'exercice précédent.
Solution
Question 5)
En dériver l'expression de 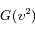 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
Solution
La condition de normalisation est :
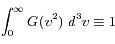
où 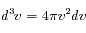 en coordonnées sphériques. Ceci donne :
en coordonnées sphériques. Ceci donne :
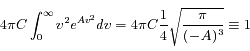
La vitesse quadratique moyenne donne :
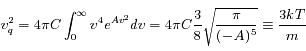
Le rapport des deux conditions conduit à :
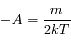 d'où
d'où 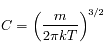
On en conclut :
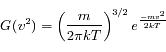
Question 6)
En dériver l'expression de 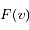 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.
Solution
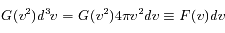
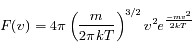
qu'on appelle distribution de Maxwell-Boltzman.
Question 7)
Tracer cette fonction, expliquer sa forme.
Solution
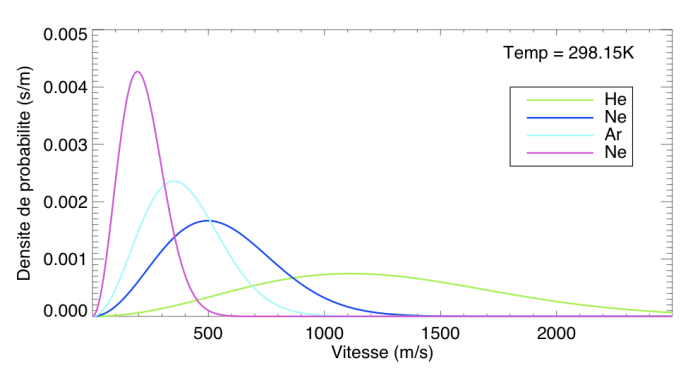
Distributions de Maxwell pour différents gaz rares à température ambiante.
Le maximum de la fonction n'est pas dû à la gaussienne elle-même (il est loin de la moyenne de celle-ci qui est centrée), mais au produit de la queue de la gaussienne par un polynôme de degré 2.
Question 8)
Comment peut-on utiliser cette fonction pour expliquer l'évolution des atmosphères planétaires ?
Solution
En utilisant la température qui règne au sommet de l'atmosphère, la fonction permet de calculer la distribution de vitesse des différentes espèces moléculaires ou atomiques. On peut comparer celle-ci à la vitesse d'échappement de la planète, qui dépend de sa gravité et de son rayon (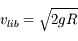 ).
).
Si une fraction significative des molécules a une vitesse supérieure à la vitesse de libération, cette espèce s'échappera rapidement de la haute atmosphère — c'est la raison première pour laquelle la Lune n'a pas d'atmosphère, alors que la Terre conserve la sienne à la même distance du Soleil.
En dehors de ce mécanisme d'échappement thermique, il existe d'autres mécanismes d'échappement atmosphérique.


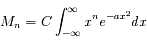
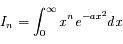
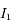 . Que représente cette quantité ?
. Que représente cette quantité ?
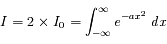
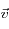 et
et 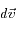 est notée
est notée 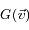 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
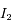 et
et 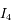 de l'exercice précédent.
de l'exercice précédent.
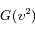 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
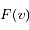 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.