images/logos_obspm_lille1.png

L'Astronomie dans l'apprentissage des Mathématiques

L'Astronomie dans l'apprentissage des Mathématiques

Intégrale de Riemann

Intégrales Généralisées

• Loi de Stefan

• Ex : loi de Stefan

• Distribution des vitesses de Maxwell

• Ex: Distribution des vitesses de Maxwell

• Temps de vie d'une étoile

• Ex: Temps de vie d'une étoile

Ex : loi de Stefan

Auteurs: Marc Fouchard, Stéphane Erard, S. Renner

Auteur: Marc Fouchard

loi de Stefan

Difficulté : ☆☆ Temps : 1h

Question 1)

Sachant que 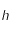, 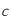et 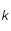sont des constantes strictement positives et que la température 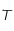étant mesurée en degré Kelvin est aussi strictement positive, montrer que 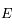est de classe 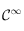${\mathcal C}^{\infty}$ sur $]0,+\infty[$ et est toujours strictement positive sur cet intervalle.

Question 2)

L'énergie totale 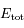$E_{\rm tot}$ est donnée par :

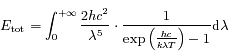$E_{\rm tot}=\int_0^{+\infty} \frac{2 h c^2}{\lambda ^5}\cdot \frac{1}{\exp \left( \frac{h c}{k \lambda T} \right) -1}{\rm d} \lambda$ .

Montrer, en effectuant un changement de variable approprié, que 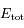$E_{\rm tot}$ peut s'écrire sous la forme:

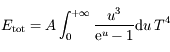
$E_{\rm tot}=A \int_0^{+ \infty} \frac{u^3}{{\rm e}^u-1}{\rm d} u \,T^4$

où 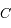est une constante que l'on déterminera.

Question 3)

Montrer que l'intégrale

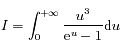
$I=\int_0^{+\infty}\frac{u^3}{{\rm e}^u-1}{\rm d} u$

est convergente.

Remarque

Cette intégrale est une fonction zeta de Reimann. On peut montrer que 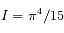$I=\pi^4/15$ .

Question 4)

En déduire la loi de Stefan:

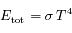
$E_{\rm tot}=\sigma \, T^4$

où 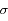$\sigma$ est une constante que l'on déterminera.