Ex: Temps de vie d'une étoile

Auteurs: Marc Fouchard, Stéphane Erard, S. Renner

Auteur: S. Renner

Temps de vie d'une étoile

Difficulté : ☆ Temps : 1h

On assimile l'étoile à une sphère homogène de masse 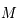et de rayon .

Question 1)

Montrer que son énergie de liaison gravitationnelle est $E_G = - \frac{3}{5} \frac{GM^2}{R}$ .

Aide Solution

Question 2)

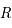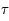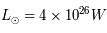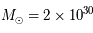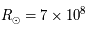En déduire le temps de vie $\tau$ du Soleil sur ses seules ressources gravitationnelles. On rappelle que la luminosité (puissance totale rayonnée) du Soleil est $L_\odot = 4 \times 10^{26} W$ , sa masse $M_\odot = 2 \times 10^{30}$ kg et son rayon $R_\odot = 7 \times 10^8$ m.

Solution

Question 3)

Même question en considérant le cas réel des réactions de fusion nucléaire de l'hydrogène en hélium au coeur du Soleil. On suppose que 10% de la masse 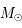$M_\odot$ est convertie en hélium et que la luminosité 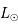$L_\odot$ reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie E = m c^2 .

Solution

Question 4)

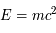Le Soleil brille depuis 4.5 milliards d'années. Combien a t-il perdu en masse ?

Solution