Loi de Stefan

Auteurs: Marc Fouchard, Stéphane Erard, S. Renner

Auteur : Marc Fouchard

La loi de Planck montre que pour un corps noir, l'énergie émise par rayonnement suivant une longueur d'onde, ne dépend que de la température de surface du corps noir. Cette loi est donnée par la relation suivante :

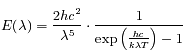
$E(\lambda)=\frac{2 h c^2}{\lambda ^5}\cdot \frac{1}{\exp \left( \frac{h c}{k \lambda T} \right) -1}$

où 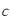correspond à la vitesse de la lumière dans le vide, 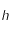est la constante de Planck, 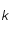la constante de Boltzmann, 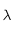$\lambda$ la longueur d'onde à laquelle le rayonnement est émis et 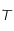la température de surface du corps noir.

La figure ci dessous montre le comportement de 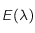$E(\lambda)$ pour différente température de surface du corps noir. Sachant que l'énergie totale 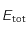$E_{\rm tot}$ émise par le corps noir par seconde et par unité de surface correspond à l'aire comprise en l'axe des abcisses et la courbe, on remarque que 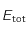$E_{\rm tot}$ augmente avec la température de surface du corps noir (il ne faut pas cocher la case "normaliser").

Le but de cet exercice est d'établir la relation exacte entre 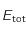$E_{\rm tot}$ et la température de surface 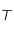du corps noir.

Loi de Planck

Crédit : Astrophysique sur Mesure

Remarque

On pourra aussi voir cet exercice en lien avec la loi de Planck pour les corps noirs.