Auteur: Stéphane Erard

 Bruit de numérisation
Bruit de numérisation
Difficulté : ☆
Temps : 30 min
L'exercice consiste à estimer l'erreur due à la numérisation (ou quantification) d'un signal continu.
Question 1)
On mesure un signal lumineux avec une caméra CCD. Tracer l'allure de la fonction de réponse du convertisseur analogique/numérique (CAN). Si le convertisseur fonctionne sur 12 bits, combien de valeurs sont disponibles en sortie ?
Le convertisseur est réglé pour couvrir la dynamique de la caméra jusqu'à un niveau analogique 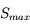 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?
Solution
Le signal d'entrée, continu, est mesuré par le CCD puis numérisé par le CAN. La sortie est donc discrète, codée sur 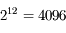 niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
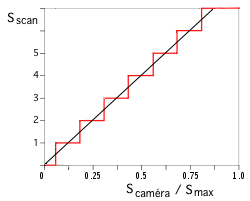
La courbe de réponse donne la sortie du système de mesure en fonction de son entrée :
Numérisation
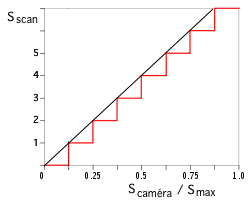
Sur n bits, le pas de numérisation du signal de sortie est q = 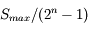
Question 2)
Estimer l'erreur quadratique moyenne due à la numérisation.
AideSolution
L'erreur est la différence entre le signal d'entrée et le signal de sortie, similaire à une erreur d'arrondi :
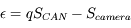
On commence par corriger de l'erreur systématique (biais, ou offset) en centrant la différence — ce biais est de 1/2 pas-codeur :
Offset
L'erreur quadratique moyenne se calcule de façon classique :
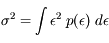
Après correction du biais, la densité de probabilité de l'erreur est uniforme dans l'intervalle [-q/2, q/2] :
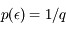 dans l'intervalle [-q/2, q/2]
dans l'intervalle [-q/2, q/2]
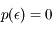 ailleurs
ailleurs
Erreur de numérisation
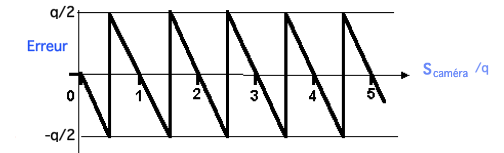
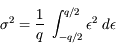
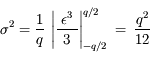
Soit un écart-type 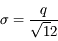 ou encore
ou encore 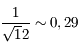 bits.
bits.
(on remarque que le coefficient 1/12 provient de l'intégration, et n'a rien à voir avec le nombre de bits utilisés)
Question 3)
Calculer le rapport signal sur bruit correspondant. Comment peut-on améliorer celui-ci, et jusqu'à quel point ?
Solution
Le signal maximum est 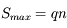 . En rapportant au signal moyen, on trouve :
. En rapportant au signal moyen, on trouve :
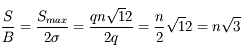
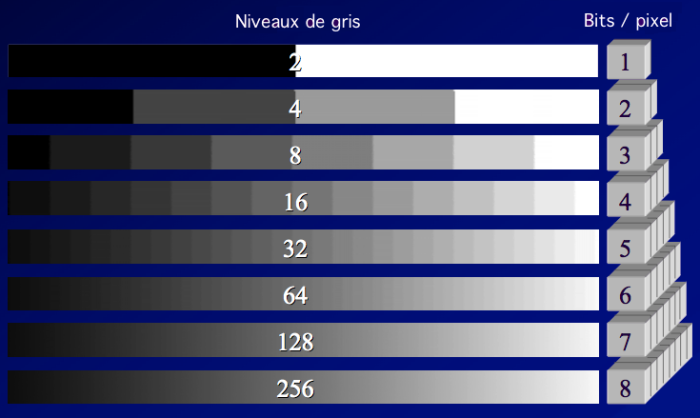
La seule façon de réduire le bruit de numérisation est de coder le signal sur un plus grand nombre de bits n. La différence de "grain" est très perceptible à l'œil nu avec une échelle de gris codée sur un nombre variable de bits. A partir de 256 niveaux, la variation apparaît quasiment continue, ce qui veut dire que le pas de quantification devient petit devant l'incertitude de lecture de l'œil. De la même façon, les CD audio sont codés sur 16 bits pour éliminer le bruit de numérisation ; celui-ci est encore très audible avec un codage sur 8 bits.
Résolution numérique
Question 4)
Comparer aux autres sources de bruit.
Solution
On ajuste habituellement le pas de numérisation pour coder le bruit physique sur 1 pas-codeur : un pas plus petit n'apporterait pas d'information supplémentaire sur le signal. En général, c'est le bruit de lecture qui domine le bruit intrinsèque de la source (bruit de photon). Le bruit de numérisation est alors bien plus petit. Si la chaîne de détection est bien réglée, celui-ci ne limite donc jamais la mesure.


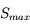 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?