

Ex: Supernova 1A |
Difficulté : ☆ Temps : 30 min
On observe une supernova de type 1A dans une galaxie et on mesure sa magnitude apparente 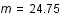 . Grâce à sa courbe de lumière, on détermine sa magnitude absolue
. Grâce à sa courbe de lumière, on détermine sa magnitude absolue 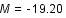 .
.
On exprime la distance luminosité, 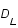 , comme suit:
, comme suit:
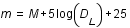 , où
, où 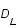 est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à
est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à 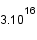 m).
m).
Calculer sa valeur.
La distance de la galaxie est par définition:
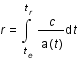 , où c est la vitesse de la lumière, t le temps,
, où c est la vitesse de la lumière, t le temps, 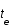 le temps d'émission de la lumière par la galaxie,
le temps d'émission de la lumière par la galaxie, 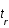 celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
Sachant que le facteur d'échelle est relié au redshift, z, par la relation suivante, 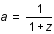 et que par définition la constante de Hubble vaut
et que par définition la constante de Hubble vaut 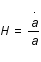 ; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à
; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à 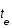 ,
, 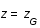 et par définition à
et par définition à 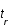 , z=0).
, z=0).
Calculer r, puis sachant que la distance luminosité et la distance r sont reliées par la relation 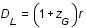 (dans le modèle cosmologique standart
(dans le modèle cosmologique standart 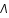 CDM), déterminer l'équation du second degré à laquelle obéit
CDM), déterminer l'équation du second degré à laquelle obéit 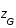 .
.
Résoudre cette équation et déterminer la valeur du redshift 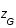 (positive par définition).
On donne
(positive par définition).
On donne  et
et 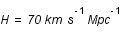 .
.