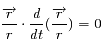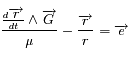Auteur: Alain Vienne
Quand on formule le problème des 2-corps, on arrive au problème de Képler, c'est-à-dire à l'équation différentielle vectorielle suivante:
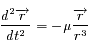
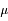 est une constante réelle positive et
est une constante réelle positive et 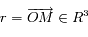 .
. 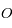 est un point fixe et on étudie le mouvement de
est un point fixe et on étudie le mouvement de 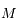 .
.
Les deux exercices proposés donnent la loi des aires et l'intégrale de Laplace.
En fait, le premier exercice aura 2 conséquences: la première est que le mouvement est plan et la deuxième que la loi du mouvement est la loi des aires proprement dite:
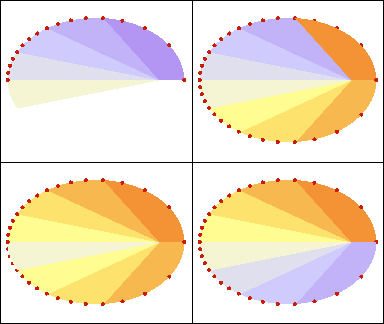
La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
Auteur: Alain Vienne
 La loi des aires
La loi des aires
Difficulté : ☆
Temps : 20mn
 Introduction
Introduction
La loi des aires est très facile à obtenir avec le produit vectoriel. Sans le produit vectoriel, on peut aller voir cet exercice.
Question 1)
Montrer que dans le problème képlérien, le moment cinétique:
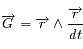
est invariant.
Dériver 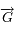 et utiliser que
et utiliser que 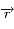 et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
Question 2)
Montrer que le mouvement de 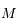 se fait dans un plan passant par le point
se fait dans un plan passant par le point 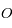 et orthogonal à
et orthogonal à 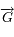 .
.
Question 3)
En utilisant un élément d'aire 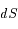 parcouru par
parcouru par 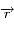 pendant l'élément de temps
pendant l'élément de temps 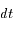 , montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
, montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
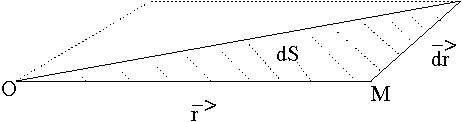
L'aire 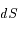 est la moitié du parallélogramme suivant:
est la moitié du parallélogramme suivant:
Auteur: Alain Vienne
 Intégrale de Laplace
Intégrale de Laplace
Difficulté : ☆
Temps : 20mn
Question 1)
Montrer l'expression suivante:
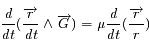
Partir du premier membre de l'expression et utiliser le problème de képler et l'invariance du moment cinétique.
Remarquer que 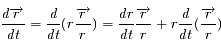
Utiliser que 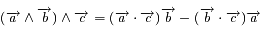
La norme de 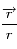 est constante donc
est constante donc 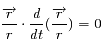
Question 2)
Déduire de l'égalité précédente une expression qui est constante pendant le mouvement (intégrale de Laplace).
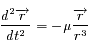
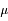 est une constante réelle positive et
est une constante réelle positive et 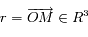 .
. 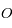 est un point fixe et on étudie le mouvement de
est un point fixe et on étudie le mouvement de 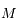 .
.

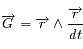
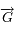 et utiliser que
et utiliser que 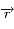 et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
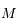 se fait dans un plan passant par le point
se fait dans un plan passant par le point 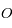 et orthogonal à
et orthogonal à 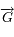 .
.
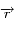 et
et 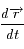 sont toujours (quelque soit le temps) orthogonaux à
sont toujours (quelque soit le temps) orthogonaux à 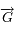 , avec l'hypothèse toutefois que
, avec l'hypothèse toutefois que 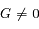 .
.
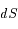 parcouru par
parcouru par 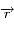 pendant l'élément de temps
pendant l'élément de temps 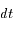 , montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
, montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
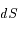 est la moitié du parallélogramme suivant:
est la moitié du parallélogramme suivant:
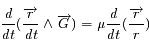
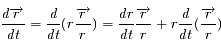
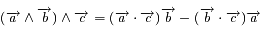
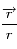 est constante donc
est constante donc