La loi des aires

Auteurs: Alain Vienne, S. Renner

Auteur: Alain Vienne

La loi des aires dit que, dans le problème de l'interaction gravitationnelle de deux corps, l'aire balayée par le rayon vecteur est proportionnel au temps. Cette loi est aussi appelée "deuxième loi de Kepler" (voir aussi dans ce même chapitre, le lien suivant).

La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales. Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.

Crédit : Astrophysique sur Mesure

En fait, la loi des aires est plus générale que la deuxième loi de Kepler puisque qu'elle s'applique pour toute force centrale. Pour la démontrer, il faut bien-sur utiliser la loi fondamentale de la dynamique:

Principe fondamental de la dynamique

L'accélération d'un mobile est proportionnelle à la force à laquelle il est soumis.

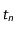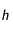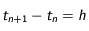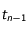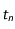La preuve qui est proposée en exercice utilise un modèle discret. Elle est directement inspirée d'une application isssue du livre de Daniel Perrin "Nombre, mesures et géométrie" (Ed. CASSINI). Ainsi le temps est une juxtaposition d'instants t_n de durée très courte de telle sorte que $t_{n+1}-t_n=h$ . 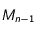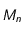La discrétisation revient à supposer qu'entre les instants $t_{n-1}$ et t_n , le mobile se déplace de $M_{n-1}$ à M_n avec la vistesse constante 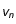v_n . En vecteur la vistesse est donc 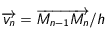$\overrightarrow{v_n}=\overrightarrow{M_{n-1}M_n}/h$ . 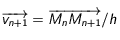Sur l'intervalle suivant $[t_n,t_{n+1}]$ , la vitesse est différente mais constante aussi pour cette durée: $\overrightarrow{v_{n+1}}=\overrightarrow{M_nM_{n+1}}/h$ . 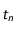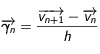Ainsi à l'instant t_n l'accélération est $\overrightarrow{\gamma_n}=\frac{\overrightarrow{v_{n+1}}-\overrightarrow{v_n}}{h}$ .

Crédit : Astrophysique sur Mesure / Vienne

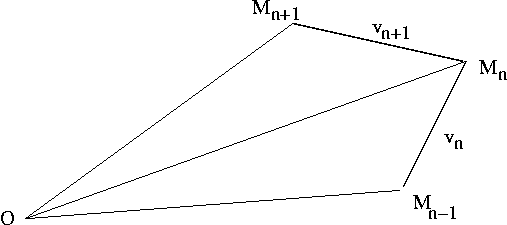
Le modèle continu s'obtient facilement par passage à la limite.

La loi fondamentale de la dynamique s'écrit alors: 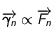$\overrightarrow{\gamma_n} \propto \overrightarrow{F_n}$

Les outils mathématiques nécéssaires à cette preuve se limitent alors à deux petits lemmes que Daniel Perrin nomment lemmes de découpage et que nous admettrons:

Lemme du demi-parallélogramme :

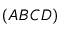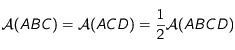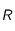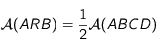Soit (ABCD) un parallélogramme. La diagonale [AC] partage le parallélogramme en deux triangles de même aire: $\mathcal A (ABC) = \mathcal A (ACD) = \frac{1}{2} \mathcal A (ABCD)$ . Plus généralement, pout tout point de [CD] , on a : $\mathcal A (ARB) = \frac{1}{2} \mathcal A (ABCD)$ .

Lemme de la médiane :

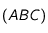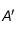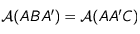Soit (ABC) un triangle et le milieu de [BC] . La médiane [AA'] partage le triangle en deux triangles de même aire: $\mathcal A (ABA') = \mathcal A (AA'C)$ .