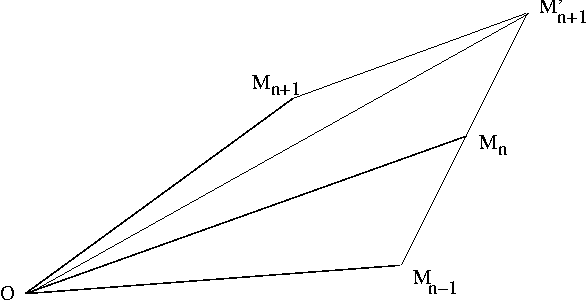
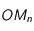 |  |  |  |  |  |
Ex: La loi des aires |
La loi des airesDifficulté : ☆☆ Temps : 1h
Introduction
Le mobile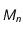 
est soumis à une force centrale, c'est-à-dire dirigée vers un point 
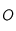fixe (le Soleil par exemple si la masse de 
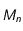est négligeable par rapport à celle du Soleil): la force est 
.
Remarque
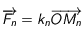Il n'y a aucune hypothèse nécessaire sur le réel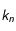 
même si on sait que pour la loi de Newton ce scalaire est négatif et inversement proportionnel au carré de la distance 
 |  |
), on a: 
est proportionnel au temps parcouru.
et 
(vitesses du mobile aux temps 
et 
) et considérer le point 
qu'occuperait le mobile au temps 
si le mouvement était uniforme.
pour avoir 
, puis prendre 
de telle manière que 
soit un parallélogramme et enfin lui appliquer le lemme correspondant avec 
puis avec 
.
