 |  |  |  |  |  |
Equation de Kepler |
Auteur: S. Renner
Date de création: 16 mai 2013
On reprend les résultats obtenus dans l'exercice sur la résolution du problème des 2 corps. Le but ici est d'établir l'équation de Kepler à l'aide de la géométrie essentiellement, plutôt que par le calcul.
L'équation de Kepler (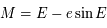
) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne 
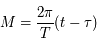, avec 
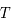la période orbitale, 
le temps et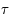 
l'instant de passage au péricentre.
 |  |
