 |  |  |  |  |  |
Ex: Vitesse orbitale de la Terre |
Vitesse orbitale de la TerreDifficulté : ☆ Temps : 1h30
On fait l'hypothèse que l'orbite de la Terre est circulaire est que celle-ci est décrite avec une vitesse uniforme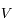 
.
On note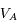 
la vitesse radiale d'Arcturus par rapport au Soleil (supposée identique aux instants 
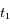et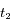 
). Ecrire en fonction de 
, 
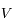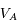et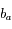 
la vitesse radiale d'Arcturus par rapport à l'observateur à l'instant 
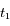(on notera cette vitesse 
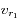), ainsi qu'à l'instant 
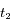(notée 
).
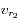En appliquant la formule de l'effet Doppler-Fizeau aux instants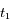 
et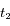 
pour la longueur d'onde de référence 
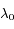, écrire les expressions de 
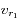et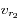 
.
En déduire l'expression de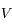 
et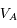 
en fonction des longueurs d'onde 
, 
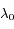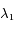et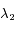 
. Calculer leur valeur numériquement en km.s
.
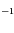Calculer la distance Terre-Soleil en km sachant que la période de révolution est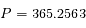 
jours.
 |  |
(angle entre la direction de l'étoile et le plan de l'écliptique).
Remarque
. Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module 
.
, 
, 
, donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant 
et 
, donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant 
et 
(1)
(2)
![\Longrightarrow V_A=\frac{c}{2 \lambda_0} [ (\lambda_1 - \lambda_0) + (\lambda_2 - \lambda_0) ]](../pages_applications/equations_applications/equation104.png)
![\Longrightarrow V=\frac{c}{2 \lambda_0 \cos b_a} [ (\lambda_2 - \lambda_0) - (\lambda_1 - \lambda_0) ]](../pages_applications/equations_applications/equation105.png)
km.s
km.s
km.
, où 
croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence 
sera 
. Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer 
.
). L'effet de décalage est d'autant plus important que 
est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.