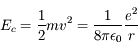
L'équation précédente donne directement l'énergie cinétique :

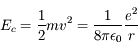
E_c = \frac{1}{2}mv^2 = \frac{1}{8\pi\epsilon_0} \frac{e^2}{r}

La situation est formellement identique au problème à deux corps en mécanique céleste, on a dans les deux cas une force attractive en 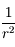\frac{1}{r^2} , qui dérive d'un potentiel en 1/r.

Le potentiel s'écrit 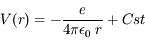V(r) = -\frac{e}{4\pi\epsilon_0\;r} + Cst

En prenant un potentiel nul à l'infini (électron détaché du noyau), la constante d'intégration est nulle.

L'énergie potentielle est donc 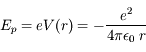E_p = eV(r) = -\frac{e^2}^{4\pi\epsilon_0\;r}

et l'énergie totale vaut 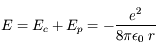E = E_c + E_p = -\frac{e^2}{8\pi\epsilon_0\;r}

Rien dans ce modèle n'implique de quantification de la distance électronique ou de l'énergie.