

Ex : le problème de 2 corps |
Difficulté : ☆☆ Temps : 2h
Montrer que 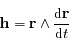 est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
En utilisant les coordonnées polaires 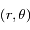 où
où 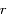 est la norme de
est la norme de 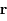 et
et 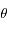 est l'angle en radian entre une direction fixe et
est l'angle en radian entre une direction fixe et 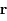 compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit
compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit 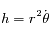 , où le point
, où le point  désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
En multipliant scalairement l' équation du mouvement par 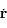 (qui n'est rien d'autre que le vecteur vitesse), montrer que
(qui n'est rien d'autre que le vecteur vitesse), montrer que
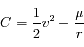 est une constante du mouvement (
est une constante du mouvement (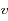 désignant la norme du vecteur vitesse).
désignant la norme du vecteur vitesse). 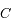 s'appelle l'intégrale de l'énergie.
s'appelle l'intégrale de l'énergie.
En utilisant les coordonnées polaires montrer que l' équation du mouvement revient à résoudre le système :
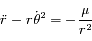
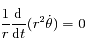
On remarquera que la deuxième équation correspond à l'intégrale du moment angulaire.
Soit 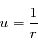 , exprimer
, exprimer 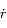 et
et 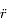 en fonction de
en fonction de 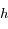 ,
, 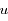 , et les dérivées première et seconde de
, et les dérivées première et seconde de 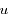 par rapport à
par rapport à 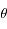 que l'on notera
que l'on notera 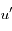 et
et 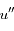 .
.
En faisant le changement de variable 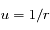 dans l'équation différentielle du second ordre obtenue pour
dans l'équation différentielle du second ordre obtenue pour 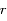 , écrire une équation linéaire du second ordre pour
, écrire une équation linéaire du second ordre pour 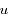 en considérant
en considérant 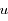 comme une fonction de
comme une fonction de 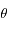 .
.
Résoudre l'équation obtenue en donnant une solution sous la forme 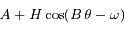 où
où 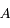 et
et 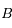 sont des constantes que l'on déterminera et
sont des constantes que l'on déterminera et 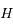 et
et 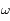 des constantes d'intégrations.
des constantes d'intégrations.
Montrer que la solution génrérale de cette équation peut s'écrire:
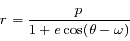 avec
avec 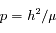 ,
, 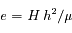 et
et 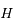 et
et 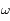 sont deux constantes d'intégration.
sont deux constantes d'intégration.
Pour 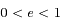 , on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité
, on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité  et de demi-grand axe
et de demi-grand axe 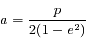 mais ceci fait l'objet d'un autre exercice.
mais ceci fait l'objet d'un autre exercice.
On peut cependant remarquer que dans ce cas les valeurs minimale et maximale de 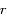 sont
sont 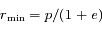 et
et 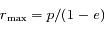 et sont obtenues pour
et sont obtenues pour 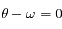 et
et 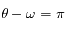 respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre,
respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre, 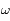 donnant la direction du pericentre et
donnant la direction du pericentre et 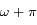 celle de l'apocentre.
La distance séparant ces deux positions est donc
celle de l'apocentre.
La distance séparant ces deux positions est donc 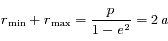 , où
, où 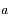 est ce qu'on appelle le demi-grand axe.
est ce qu'on appelle le demi-grand axe.