Ex: Détermination du potentiel dans une sphère de Debye

Auteurs: Arnaud Beck, Marc Fouchard, S. Renner, Florent Deleflie, Alain Vienne

Auteur: Arnaud Beck

Détermination du potentiel dans une sphère de Debye

Question 1)

On considère un ion en 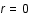r=0 et soit 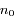$n_{\rm 0}$ la densité ionique moyenne dans le plasma. Si le plasma est suffisamment chaud, on peut montrer que la densité électronique est égal à

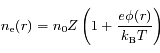
$n_{\rm e}(r)=n_{\rm 0}Z\left(1+\frac{e\phi(r)}{k_{\rm B}T}\right)$

où 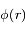$\phi(r)$ est le potentiel en 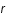, 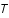la température du plasma et 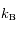$k_{\rm B}$ la constante de Boltzmann.

Par ailleurs, l'équation de Poisson relie la densité de charge 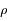$\rho$ et le potentiel 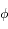$\phi$ de la manière suivante:

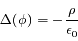
$\Delta(\phi)=-\frac{\rho}{\epsilon_{\rm 0}}$

1) Écrire l'équation différentielle vérifiée par le potentiel 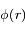$\phi (r)$ sous la forme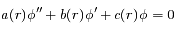 $a(r)\phi ''+b(r)\phi ' +c(r)\phi=0$

2) Trouver un changement de variable 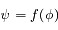$\psi=f(\phi)$ tel que l'équation différentielle du second ordre vérifiée par 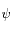$\psi$ soit à coefficients constants.

3) Trouver la forme du potentiel 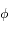$\phi$ . Les conditions aux limites sont que le potentiel 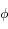$\phi$ doit tendre vers 0 lorsque 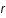tend vers l'infini et il doit être équivalent au potentiel Coulombien lorsque 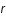tend vers 0. En déduire la distance caractéristique d'écrantage de la charge centrale (longueur de Debye) dans ce cas.

Solution