Du second ordre
Auteurs: Arnaud Beck, Marc Fouchard, S. Renner, Florent Deleflie, Alain Vienne
- Pendule et équation de Mathieu
- Ex: Pendule et équation de Mathieu
- Longueur de Debye
- Ex: Détermination du potentiel dans une sphère de Debye
- Le problème de 2 corps
- Ex : le problème de 2 corps
- Train gravitationnel
- Ex: Train gravitationnel
- Pendule de Foucault
- Ex: Pendule de Foucault
Pendule et équation de Mathieu
Auteur: Alain Vienne
Beaucoup de modèles dynamiques, après maintes transformations (hypothèses simplificatrices, moyennisations, ...), ressemblent au modèle du pendule (masse à une distance constante d'un point fixe sous l'effet de la pesanteur). Ici nous allons nous intéresser à un type d'équation du pendule correspondant à l'équation de Mathieu:
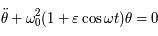
Si 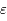 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 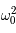 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 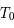 est alors
est alors 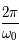 .
.
Ici 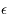 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
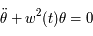
où 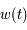 est une fonction périodique de période
est une fonction périodique de période 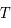 qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
De manière plus ludique, ces équations peuvent modéliser le mouvement d'une balançoire dont le passager se lève et s'assied (périodiquement) afin de s'élancer. Le fait de se lever et de s'assoir régulièrement revient à déplacer le centre de gravité du passager et donc, revient à faire varier périodiquement la longueur du pendule (ici la balançoire).
L'exercice qui suit ne résoud pas l'équation différentielle. Il cherche simplement à savoir dans quelles conditions la solution est bornée ou non (problème de stabilité). Il est insipré du théorème de Gustave Floquet (1847-1920).
Ex: Pendule et équation de Mathieu
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h30
On considère l'équation différentielle suivante (équation de Mathieu):
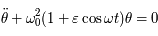
Où 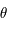 est une fonction du temps
est une fonction du temps  . Cette équation dépend des paramètres
. Cette équation dépend des paramètres 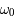 ,
, 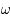 et
et 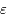 .
.
On souhaite déterminer dans quelles conditions la solution est bornée ou non.
Question 1)
Ecrire l'équation de Mathieu comme une équation différentielle du premier ordre:
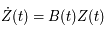
où 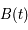 est une matrice
est une matrice 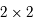 réelle. Donner la signification de la nouvelle inconnue
réelle. Donner la signification de la nouvelle inconnue 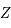 (par rapport à
(par rapport à 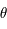 ).
).
Question 2)
On se donne une condition initiale 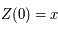 (on a
(on a 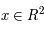 ). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note
). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note 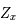
Monter que l'application 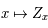 est linéaire.
est linéaire.
Question 4)
Pouvoir expliciter 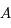 , revient à obtenir toutes les solutions de l'équation différentielle.
, revient à obtenir toutes les solutions de l'équation différentielle. 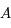 est donc une inconnue. Montrer que
est donc une inconnue. Montrer que 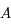 vérifie le système suivant:
vérifie le système suivant:
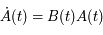
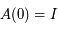
où 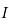 est la matrice identité.
est la matrice identité.
Question 5)
Montrer que pour tout système de la forme
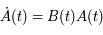
, on a le résultat suivant:
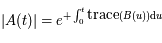
où 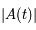 est le déterminant (d'ordre 2) de
est le déterminant (d'ordre 2) de 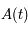 et
et 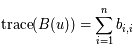 (somme des éléments diagonaux).
(somme des éléments diagonaux).
Question 7)
Montrer que:
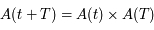
où 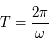
Question 8)
La matrice 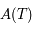 s'appelle la matrice de Floquet.
s'appelle la matrice de Floquet.
Montrer que les valeurs propres 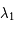 et
et 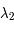 de la matrice de Floquet vérifient:
de la matrice de Floquet vérifient:
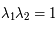
Question 9)
Ainsi, si ces valeurs propres sont réelles, l'une d'elle en valeur absolue est supérieure à 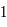 . Donc avec
. Donc avec 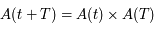 et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
Montrer que sinon (valeurs propres complexes), les solutions sont bornées.
Question 10)
Dans notre cas (équation de Mathieu), 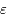 est petit. On peut alors montrer que la somme des valeurs propres de
est petit. On peut alors montrer que la somme des valeurs propres de 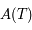 est la trace de la matrice
est la trace de la matrice 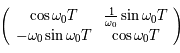 (ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
(ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
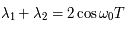
Montre que des solutions non bornées sont possibles que si la période 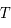 du forçage est telle que
du forçage est telle que
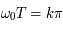
où 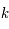 est un entier relatif.
est un entier relatif.
Longueur de Debye
Auteur: Arnaud Beck
Un plasma est une collection de particules chargées. Pour simplifier, considérons qu'il n'est composé que d'électrons de charge 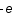 et d'ions de charge
et d'ions de charge 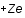 .
.
Un ion, considéré comme ponctuel, lorsqu'il est dans le vide crée autour de lui un potentiel 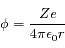 où
où 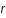 est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
Dans un plasma, il en va différemment. En effet, il va attirer autour de lui des charges de signe opposé (les électrons) qui vont écranter son potentiel. La sphère d'électrons qui se forme autour de l'ion est appelée la sphère de Debye et son rayon est appelé la longueur de Debye. C'est un paramètre fondamental en physique des plasmas.
 Remarque
Remarque
Dans cet exercice, on propose de retrouver la valeur de ce rayon et la forme du potentiel à l'intérieur de la sphère de Debye.
Ex: Détermination du potentiel dans une sphère de Debye
Auteur: Arnaud Beck
 Détermination du potentiel dans une sphère de Debye
Détermination du potentiel dans une sphère de Debye
Le problème de 2 corps
Ex : le problème de 2 corps
Auteur: Marc Fouchard
 Le problème de 2 corps
Le problème de 2 corps
Difficulté : ☆☆
Temps : 2h
Question 1)
Montrer que 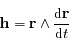 est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
Question 4)
En utilisant les coordonnées polaires montrer que l' équation du mouvement revient à résoudre le système :
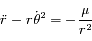
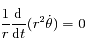
On remarquera que la deuxième équation correspond à l'intégrale du moment angulaire.
Train gravitationnel
Auteur: S. Renner
Date de création: 14 décembre 2009
L'accélération de la pesanteur dépend de la distance au centre de la Terre. Dans l'exercice qui suit, on va utiliser cette propriété pour imaginer un moyen de transport très rapide: en perçant un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, un train roulant sans frottement dans ce tunnel pourrait parcourir très rapidement la distance entre A et B. La durée du trajet, de 42 minutes environ, est même indépendante des points A et B choisis.
Ex: Train gravitationnel
Auteur: S. Renner
 Train gravitationnel
Train gravitationnel
Difficulté : ☆
Temps : 1h
On assimile la Terre à une sphère sans rotation de rayon 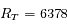 km et de masse volumique uniforme
km et de masse volumique uniforme 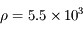
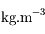 . Soit
. Soit 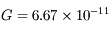 S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
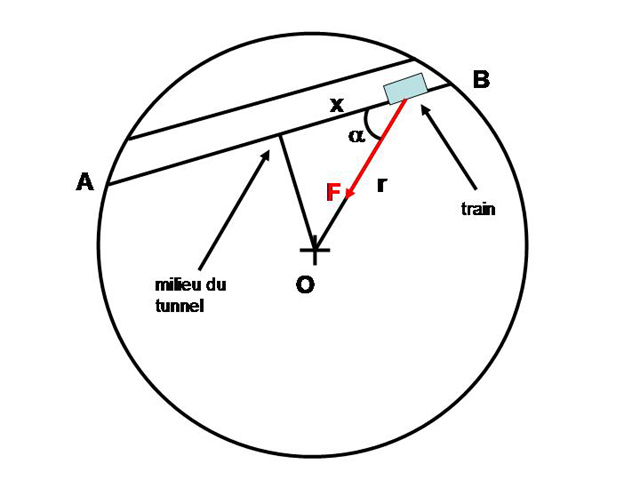
Tunnel rectiligne entre 2 points A et B de la surface terrestre. Le train est repéré par la coordonnée
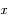
, sa distance au centre de la Terre est notée
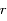
.
Question 3)
En déduire l'équation du mouvement du train dans le tunnel.
Question 4)
Le train peut-il atteindre le point B, et si oui, en combien de temps?
Pendule de Foucault
Florent Deleflie & Alain Vienne
Date de création: 21décembre 2010
Le pendule de Foucault est une expérience conçue pour mettre en évidence la rotation de la Terre, depuis un site terrestre d'observation. Son principe est basé sur la force de Coriolis qui existe dans tout réferentiel non galiléen, comme le référentiel terrestre d'observation. La réalisation de l'expérience est facilitée si la longueur du pendule est grande, comme sous le dôme d'une cathédrale par exemple. La première démonstration publique a eu lieu en 1851, sous la voûte du Panthéon, à Paris.
L'animation ci-dessous tient compte de toutes les forces sans les approximations qui seront faites dans l'exercice suivant.
Pendule de Foucault 
Ex: Pendule de Foucault
Auteur: Auteurs : Alain Vienne, Florent Deleflie.
 Pendule de Foucault
Pendule de Foucault
Difficulté : ☆☆
Temps : 1h
Le but de cet exercice est de reprendre la modélisation du pendule en tenant compte du fait que le repère terrestre n'est pas galiléen, mais est animé d'un mouvement de rotation de la Terre elle-même. La véritable motivation de l'exercice est la résolution de l'équation différentielle du mouvement.
On considère un pendule constitué d'un fil 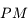 accroché en
accroché en 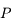 de longueur
de longueur 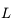 et d'une boule
et d'une boule 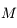 de masse
de masse 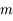 . L'espace est rapporté au système d'axes
. L'espace est rapporté au système d'axes 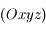 fixe dans le réferentiel lié à la Terre, l'axe
fixe dans le réferentiel lié à la Terre, l'axe 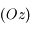 passant par
passant par 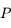 et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule
et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule 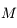 de coordonnées
de coordonnées 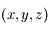 se fait dans le plan
se fait dans le plan 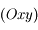 et que le module de la tension du fil
et que le module de la tension du fil 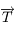 est
est 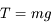 où
où 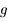 est l'accélération de la pesanteur. On note
est l'accélération de la pesanteur. On note 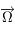 le vecteur rotation de la Terre et
le vecteur rotation de la Terre et 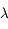 la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est
la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est 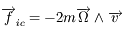 où
où 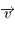 désigne la vitesse dans le repère
désigne la vitesse dans le repère 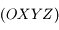 . Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de
. Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de 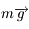 .
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans
.
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans 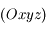 sont
sont 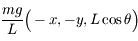 et que les composantes de la force de Coriolis sont
et que les composantes de la force de Coriolis sont 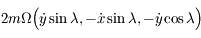 . D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur
. D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur 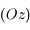 , celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant
, celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant 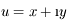 où
où 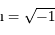 , et en posant aussi
, et en posant aussi 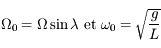 on peut montrer que l'équation du mouvement, complexe, se met sous la forme :
on peut montrer que l'équation du mouvement, complexe, se met sous la forme : 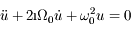 .
.
Schéma du pendule dans l'espace
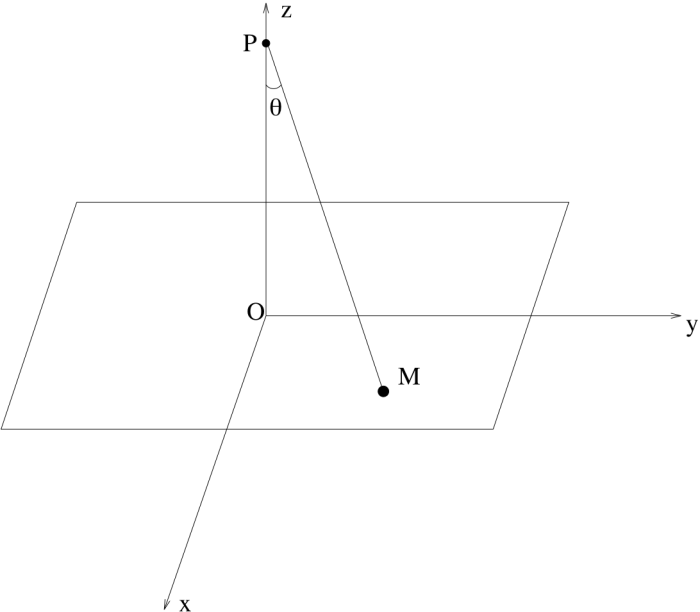
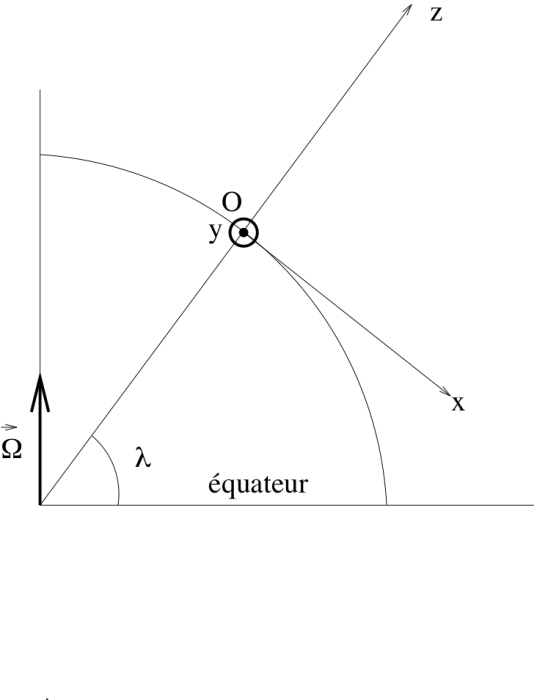
Le pendule vu dans le repère de l'observateur, et en coupe verticale.
Auteur: A. Vienne, F. Deleflie
 Pendule de Foucault
Pendule de Foucault
L'équation différentielle du mouvement qu'on se propose de résoudre est :
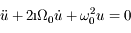
Question 1)
Ecrire le discriminant réduit de cette équation.
Question 2)
Déterminer les solutions de l'équation caractéristiques, et en déduire la forme générale de la solution de l'équation différentielle.
Question 3)
Particulariser la solution précédente en considérant qu'à l'instant initial, le mobile se trouve en 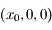 avec une vitesse initiale nulle.
avec une vitesse initiale nulle.
Question 5)
Simplifier l'expression de la solution trouvée en négligeant 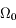 devant
devant 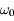 . Interpréter.
. Interpréter.
Réponses aux exercices
pages_ed-02/exo-eqmathieu.html
Exercice
-
Question 1
Solution :
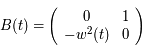 où
où 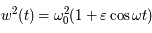 (qui est positive pour
(qui est positive pour 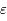 assez petit)
assez petit)
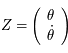
-
Question 2
Solution :
Soit 2 réels 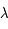 et
et 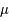 et soit 2 conditions initiales
et soit 2 conditions initiales 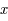 et
et 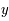 (de
(de 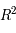 ). L'équation différentielle est linéaire donc
). L'équation différentielle est linéaire donc 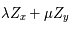 est bien UNE solution de celle-ci.
est bien UNE solution de celle-ci.
Par ailleurs,
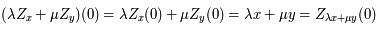
Ainsi on a bien 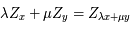
-
Question 3
Solution :
L'équation différentielle (du second ordre) à considérer est:
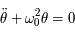
La solution générale est donc
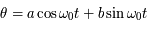
et donc:
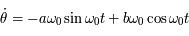
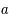 et
et 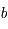 sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
La première colonne de 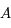 correspond à la solution de condition initiale
correspond à la solution de condition initiale 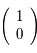 dans la notation matricielle:
dans la notation matricielle:
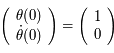
Ce qui donne 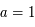 et
et 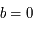 . Soit
. Soit 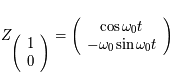
La deuxième colonne de 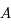 correspond à la solution de condition initiale
correspond à la solution de condition initiale 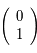 dans la notation matricielle:
dans la notation matricielle:
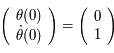
Ce qui donne 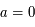 et
et 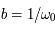 . Soit
. Soit 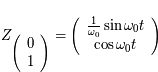
Ainsi 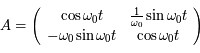
-
Question 4
Solution :
Comme 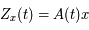 , en
, en 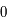 on a:
on a: 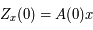 . Or, par définition,
. Or, par définition, 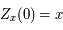 . Ainsi,
. Ainsi, 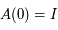 .
.
Par ailleurs, en remplaçant 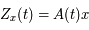 dans l'équation de Mathieu (notée matriciellement), on a:
dans l'équation de Mathieu (notée matriciellement), on a:
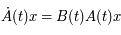
Comme cela est vrai pour tout 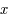 de
de 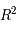 , on a bien
, on a bien 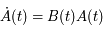 .
.
-
Question 5
Solution :
Pour un déterminant d'ordre 2, un développement direct est facile et suffit à la démonstration.
Développons 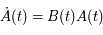 :
:
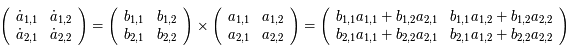
Posons 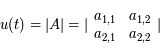 , on a:
, on a:
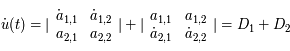
Or
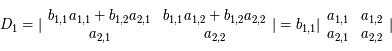
De même
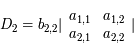
On a ainsi: 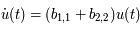 qu'il reste à intégrer. CQFD.
qu'il reste à intégrer. CQFD.
-
Question 6
Solution :
On pose encore 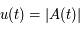 . On a:
. On a:
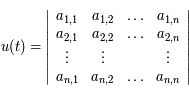
Par la forme mutilinéaire du déterminant, on 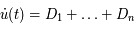 , avec
, avec
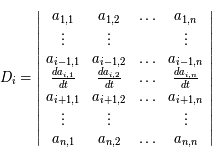
On "développe" 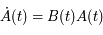 , soit:
, soit:
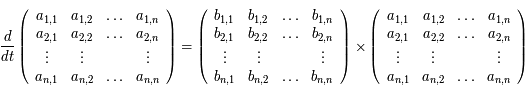
Ainsi la ligne 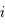 de
de 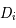 est :
est :
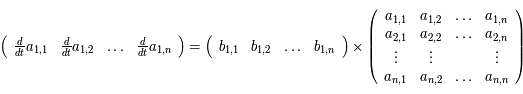
Cette ligne est donc une combinaison linéaire des lignes de 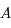 . Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
. Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
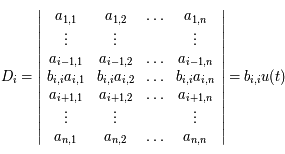
Ainsi, on a bien : 
-
Question 7
Solution :
En multipliant à droite chaque membre de la relation 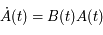 par
par 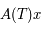 , on obtient
, on obtient
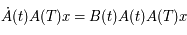
Donc 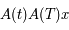 est solution de l'équation de Mathieu (sous forme matricielle:
est solution de l'équation de Mathieu (sous forme matricielle: 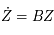 ) de condition initiale
) de condition initiale 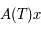 .
.
Il reste à montrer que 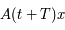 est solution aussi (avec la même condition initiale
est solution aussi (avec la même condition initiale 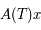 ).
).
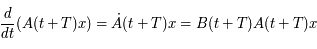
car 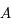 est solution de
est solution de 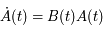 . De plus la matrice
. De plus la matrice 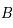 est périodique de période
est périodique de période 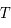 . On a finalement:
. On a finalement:
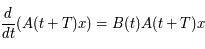
-
Question 8
Solution :
On a 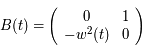 . Donc
. Donc 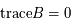 et
et 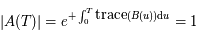
-
Question 9
Solution :
Dans ce cas, 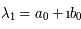 et
et 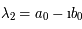 . Elles sont conjuguées car la matrice est réelle. De plus,
. Elles sont conjuguées car la matrice est réelle. De plus, 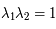 , donc
, donc 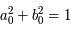 . C'est donc une matrice de rotation. Or
. C'est donc une matrice de rotation. Or 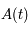 est borné sur l'intervalle borné
est borné sur l'intervalle borné 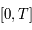 . Par la relation
. Par la relation 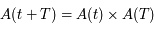 , on en déduit que
, on en déduit que 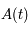 est borné sur l'ensemble des réels.
est borné sur l'ensemble des réels.
-
Question 10
Solution :
Le polynôme caractéristique est
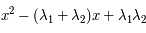
soit
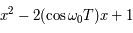
Le discrimant réduit est 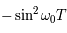 . La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
. La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
pages_ed-02/exo-ed-02.html
Exercice
'Détermination du potentiel dans une sphère de Debye'
-
Question 1
Solution :
1)
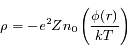
En coordonnée sphérique:
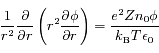
Soit 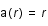 ,
, 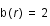 ,
, 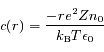 .
.
2)
On pose 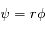 et donc
et donc 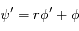 et
et 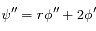
Il vient 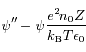
3)
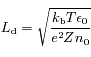
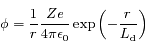
pages_ed-02/exo-pb-22-corps.html
Exercice
' Le problème de 2 corps'
pages_ed-02/exo-train-gravitationnel.html
Exercice
'Train gravitationnel'
-
Question 1
Solution :
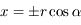
-
Question 2
Solution :
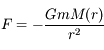 , où
, où 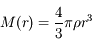 est la masse contenue à l'intérieur de la sphère de rayon
est la masse contenue à l'intérieur de la sphère de rayon 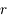 .
.
Donc 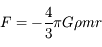 .
.
-
Question 3
Solution :
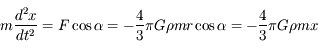 .
.
On reconnaît l'équation d'un pendule de pulsation 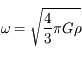 .
.
-
Question 4
Solution :
Le train peut donc atteindre le point B, la solution est périodique de période 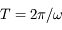 .
.
La durée du trajet est 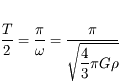 = 42 min 14 s, quels que soient les points A et B.
= 42 min 14 s, quels que soient les points A et B.
pages_ed-02/exo-pendule-foucault.html
Exercice
'Pendule de Foucault'
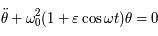
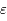 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 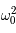 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 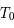 est alors
est alors 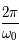 .
.
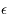 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
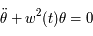
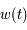 est une fonction périodique de période
est une fonction périodique de période 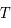 qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
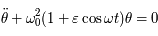
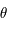 est une fonction du temps
est une fonction du temps  . Cette équation dépend des paramètres
. Cette équation dépend des paramètres 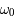 ,
, 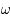 et
et 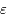 .
.
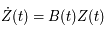
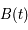 est une matrice
est une matrice 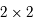 réelle. Donner la signification de la nouvelle inconnue
réelle. Donner la signification de la nouvelle inconnue 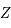 (par rapport à
(par rapport à 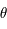 ).
).
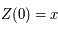 (on a
(on a 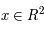 ). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note
). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note 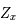
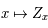 est linéaire.
est linéaire.
 donné, cette application va de
donné, cette application va de 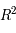 dans
dans 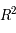 . Il existe donc une matrice
. Il existe donc une matrice 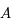 de
de 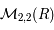 telle que
telle que 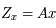 ou encore
ou encore 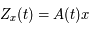 . Explciter la matrice
. Explciter la matrice 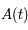 seulement dans le cas
seulement dans le cas 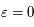 .
.
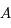 , revient à obtenir toutes les solutions de l'équation différentielle.
, revient à obtenir toutes les solutions de l'équation différentielle. 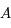 est donc une inconnue. Montrer que
est donc une inconnue. Montrer que 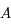 vérifie le système suivant:
vérifie le système suivant:
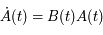
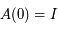
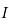 est la matrice identité.
est la matrice identité.
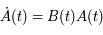
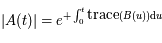
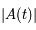 est le déterminant (d'ordre 2) de
est le déterminant (d'ordre 2) de 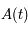 et
et 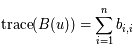 (somme des éléments diagonaux).
(somme des éléments diagonaux).
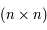 . C'est-à-dire pour
. C'est-à-dire pour 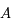 et
et 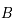 étant des matrices
étant des matrices 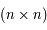 .
.
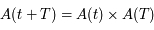
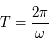
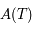 s'appelle la matrice de Floquet.
s'appelle la matrice de Floquet.
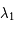 et
et 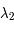 de la matrice de Floquet vérifient:
de la matrice de Floquet vérifient:
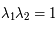
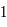 . Donc avec
. Donc avec 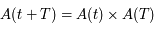 et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
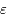 est petit. On peut alors montrer que la somme des valeurs propres de
est petit. On peut alors montrer que la somme des valeurs propres de 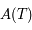 est la trace de la matrice
est la trace de la matrice 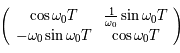 (ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
(ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
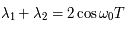
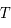 du forçage est telle que
du forçage est telle que
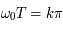
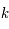 est un entier relatif.
est un entier relatif.
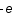 et d'ions de charge
et d'ions de charge 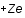 .
.
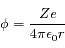 où
où 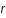 est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
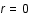 et soit
et soit 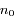 la densité ionique moyenne dans le plasma. Si le plasma est suffisamment chaud, on peut montrer que la densité électronique est égal à
la densité ionique moyenne dans le plasma. Si le plasma est suffisamment chaud, on peut montrer que la densité électronique est égal à
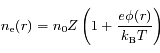
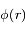 est le potentiel en
est le potentiel en 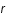 ,
, 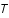 la température du plasma et
la température du plasma et 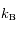 la constante de Boltzmann.
la constante de Boltzmann.
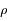 et le potentiel
et le potentiel 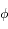 de la manière suivante:
de la manière suivante:
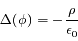
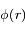 sous la forme
sous la forme 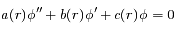
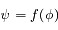 tel que l'équation différentielle du second ordre vérifiée par
tel que l'équation différentielle du second ordre vérifiée par 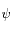 soit à coefficients constants.
soit à coefficients constants.
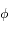 . Les conditions aux limites sont que le potentiel
. Les conditions aux limites sont que le potentiel 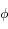 doit tendre vers 0 lorsque
doit tendre vers 0 lorsque 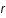 tend vers l'infini et il doit être équivalent au potentiel Coulombien lorsque
tend vers l'infini et il doit être équivalent au potentiel Coulombien lorsque 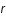 tend vers 0. En déduire la distance caractéristique d'écrantage de la charge centrale (longueur de Debye) dans ce cas.
tend vers 0. En déduire la distance caractéristique d'écrantage de la charge centrale (longueur de Debye) dans ce cas.
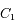 et
et 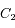 de masses respectives
de masses respectives 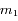 et
et 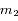 , isolés de toute autre influence, alors l'équation du mouvement de
, isolés de toute autre influence, alors l'équation du mouvement de 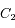 par rapport à
par rapport à 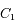 est:
est:
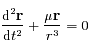
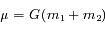 avec
avec 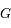 la constante universelle de la gravitation, et
la constante universelle de la gravitation, et 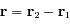 avec
avec 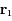 et
et 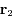 désignant les vecteurs positions des corps
désignant les vecteurs positions des corps 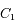 et
et 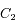 dans un repère inertiel.
dans un repère inertiel.
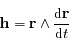 est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
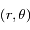 où
où 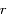 est la norme de
est la norme de 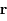 et
et 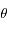 est l'angle en radian entre une direction fixe et
est l'angle en radian entre une direction fixe et 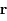 compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit
compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit 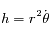 , où le point
, où le point 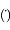 désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
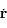 (qui n'est rien d'autre que le vecteur vitesse), montrer que
(qui n'est rien d'autre que le vecteur vitesse), montrer que
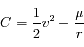 est une constante du mouvement (
est une constante du mouvement (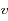 désignant la norme du vecteur vitesse).
désignant la norme du vecteur vitesse). 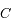 s'appelle l'intégrale de l'énergie.
s'appelle l'intégrale de l'énergie.
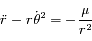
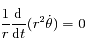
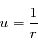 , exprimer
, exprimer 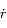 et
et 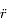 en fonction de
en fonction de 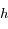 ,
, 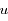 , et les dérivées première et seconde de
, et les dérivées première et seconde de 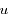 par rapport à
par rapport à 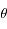 que l'on notera
que l'on notera 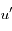 et
et 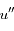 .
.
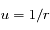 dans l'équation différentielle du second ordre obtenue pour
dans l'équation différentielle du second ordre obtenue pour 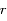 , écrire une équation linéaire du second ordre pour
, écrire une équation linéaire du second ordre pour 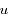 en considérant
en considérant 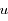 comme une fonction de
comme une fonction de 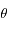 .
.
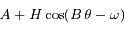 où
où 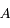 et
et 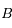 sont des constantes que l'on déterminera et
sont des constantes que l'on déterminera et 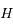 et
et 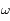 des constantes d'intégrations.
des constantes d'intégrations.
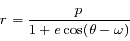 avec
avec 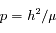 ,
, 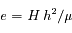 et
et 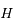 et
et 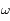 sont deux constantes d'intégration.
sont deux constantes d'intégration.
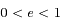 , on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité
, on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité  et de demi-grand axe
et de demi-grand axe 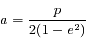 mais ceci fait l'objet d'un autre exercice.
mais ceci fait l'objet d'un autre exercice.
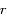 sont
sont 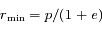 et
et 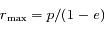 et sont obtenues pour
et sont obtenues pour 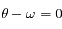 et
et 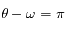 respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre,
respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre, 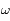 donnant la direction du pericentre et
donnant la direction du pericentre et 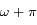 celle de l'apocentre.
La distance séparant ces deux positions est donc
celle de l'apocentre.
La distance séparant ces deux positions est donc 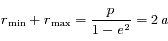 , où
, où 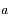 est ce qu'on appelle le demi-grand axe.
est ce qu'on appelle le demi-grand axe.
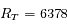 km et de masse volumique uniforme
km et de masse volumique uniforme 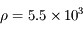
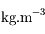 . Soit
. Soit 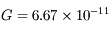 S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?

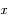 , sa distance au centre de la Terre est notée
, sa distance au centre de la Terre est notée 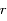 .
.
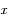 la distance du train au milieu du tunnel. Exprimer
la distance du train au milieu du tunnel. Exprimer 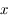 en fonction de la distance au centre de la Terre
en fonction de la distance au centre de la Terre 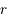 et de l'angle
et de l'angle 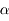 .
.
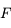 agissant sur le train en fonction de la masse du train
agissant sur le train en fonction de la masse du train 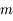 , de la masse volumique de la Terre
, de la masse volumique de la Terre 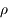 et de la distance au centre de la Terre
et de la distance au centre de la Terre 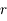 .
.

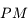 accroché en
accroché en 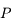 de longueur
de longueur 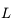 et d'une boule
et d'une boule 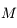 de masse
de masse 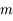 . L'espace est rapporté au système d'axes
. L'espace est rapporté au système d'axes 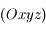 fixe dans le réferentiel lié à la Terre, l'axe
fixe dans le réferentiel lié à la Terre, l'axe 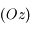 passant par
passant par 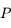 et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule
et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule 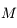 de coordonnées
de coordonnées 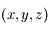 se fait dans le plan
se fait dans le plan 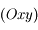 et que le module de la tension du fil
et que le module de la tension du fil 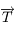 est
est 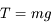 où
où 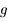 est l'accélération de la pesanteur. On note
est l'accélération de la pesanteur. On note 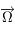 le vecteur rotation de la Terre et
le vecteur rotation de la Terre et 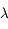 la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est
la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est 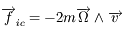 où
où 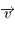 désigne la vitesse dans le repère
désigne la vitesse dans le repère 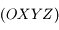 . Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de
. Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de 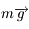 .
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans
.
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans 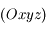 sont
sont 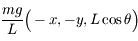 et que les composantes de la force de Coriolis sont
et que les composantes de la force de Coriolis sont 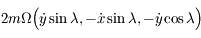 . D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur
. D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur 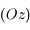 , celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant
, celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant 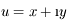 où
où 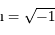 , et en posant aussi
, et en posant aussi 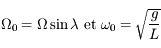 on peut montrer que l'équation du mouvement, complexe, se met sous la forme :
on peut montrer que l'équation du mouvement, complexe, se met sous la forme : 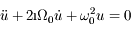 .
.


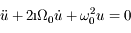
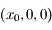 avec une vitesse initiale nulle.
avec une vitesse initiale nulle.
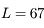 m,
m, 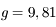 m/s2, et
m/s2, et 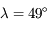 Nord. Justifier que
Nord. Justifier que 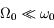 .
.
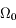 devant
devant 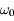 . Interpréter.
. Interpréter.
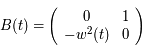 où
où 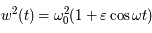 (qui est positive pour
(qui est positive pour 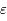 assez petit)
assez petit)
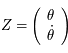
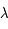 et
et 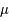 et soit 2 conditions initiales
et soit 2 conditions initiales 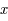 et
et 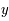 (de
(de 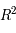 ). L'équation différentielle est linéaire donc
). L'équation différentielle est linéaire donc 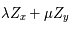 est bien UNE solution de celle-ci.
est bien UNE solution de celle-ci.
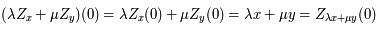
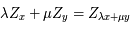
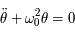
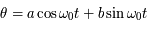
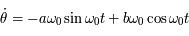
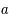 et
et 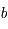 sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
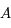 correspond à la solution de condition initiale
correspond à la solution de condition initiale 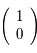 dans la notation matricielle:
dans la notation matricielle:
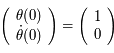
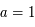 et
et 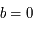 . Soit
. Soit 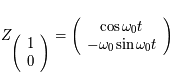
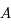 correspond à la solution de condition initiale
correspond à la solution de condition initiale 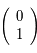 dans la notation matricielle:
dans la notation matricielle:
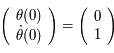
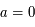 et
et 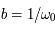 . Soit
. Soit 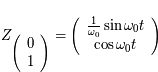
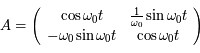
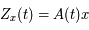 , en
, en 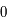 on a:
on a: 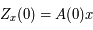 . Or, par définition,
. Or, par définition, 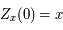 . Ainsi,
. Ainsi, 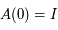 .
.
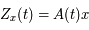 dans l'équation de Mathieu (notée matriciellement), on a:
dans l'équation de Mathieu (notée matriciellement), on a:
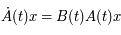
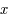 de
de 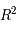 , on a bien
, on a bien 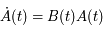 .
.
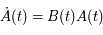 :
:
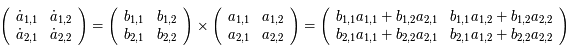
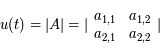 , on a:
, on a:
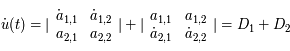
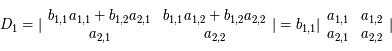
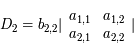
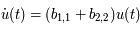 qu'il reste à intégrer. CQFD.
qu'il reste à intégrer. CQFD.
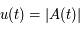 . On a:
. On a:
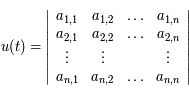
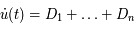 , avec
, avec
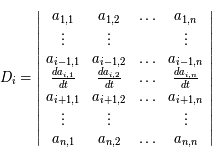
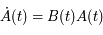 , soit:
, soit:
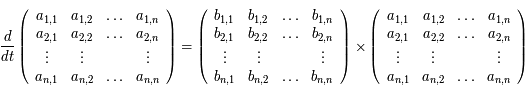
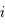 de
de 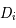 est :
est :
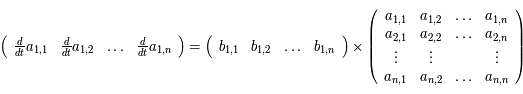
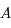 . Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
. Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
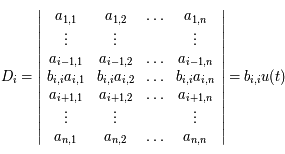

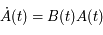 par
par 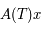 , on obtient
, on obtient
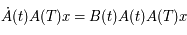
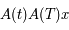 est solution de l'équation de Mathieu (sous forme matricielle:
est solution de l'équation de Mathieu (sous forme matricielle: 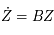 ) de condition initiale
) de condition initiale 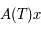 .
.
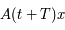 est solution aussi (avec la même condition initiale
est solution aussi (avec la même condition initiale 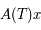 ).
).
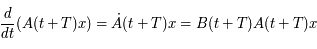
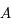 est solution de
est solution de 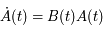 . De plus la matrice
. De plus la matrice 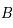 est périodique de période
est périodique de période 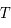 . On a finalement:
. On a finalement:
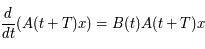
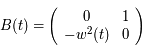 . Donc
. Donc 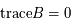 et
et 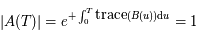
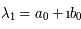 et
et 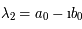 . Elles sont conjuguées car la matrice est réelle. De plus,
. Elles sont conjuguées car la matrice est réelle. De plus, 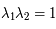 , donc
, donc 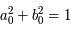 . C'est donc une matrice de rotation. Or
. C'est donc une matrice de rotation. Or 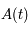 est borné sur l'intervalle borné
est borné sur l'intervalle borné 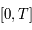 . Par la relation
. Par la relation 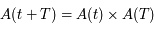 , on en déduit que
, on en déduit que 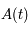 est borné sur l'ensemble des réels.
est borné sur l'ensemble des réels.
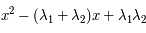
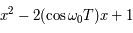
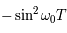 . La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
. La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
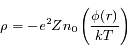
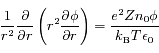
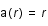 ,
, 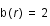 ,
, 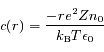 .
.
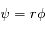 et donc
et donc 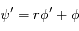 et
et 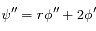
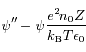
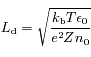
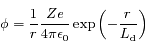
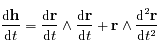 or
or 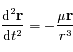 et le produit vectoriel de deux vecteurs colinéaires est nul donc
et le produit vectoriel de deux vecteurs colinéaires est nul donc
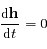 .
.
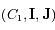 un repère orthonormal direct du plan tel que les angles sont mesurés à partir du vecteur
un repère orthonormal direct du plan tel que les angles sont mesurés à partir du vecteur 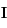 . Dans ce repère on a
. Dans ce repère on a 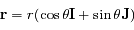 et
et 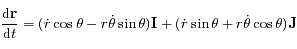 .
Ainsi, sachant que
.
Ainsi, sachant que 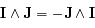 et que
et que 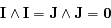 on a
on a 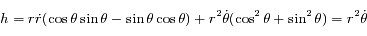 .
.
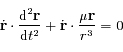 .
.
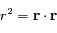 et
et 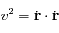 , on remarque que :
, on remarque que :
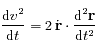 et
et 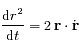 .
.
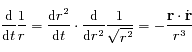
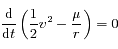 ,
,
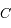 est bien une constante du mouvement.
est bien une constante du mouvement.
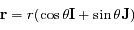 et
et 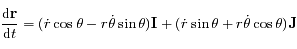 .
.
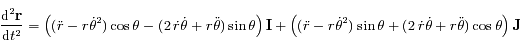 .
.
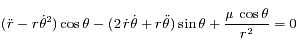
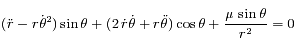
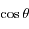 et la deuxième par
et la deuxième par 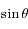 et en sommant les deux équations obtenues d'une part ; et en multipliant la première équation par
et en sommant les deux équations obtenues d'une part ; et en multipliant la première équation par 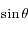 et la deuxième par
et la deuxième par 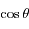 et en soustrayant les deux équations obtenues d'autre part ; on obtient le système suivant:
et en soustrayant les deux équations obtenues d'autre part ; on obtient le système suivant:
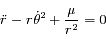
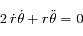
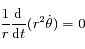 .
.
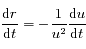 or l'intégrale du moment angulaire implique que
or l'intégrale du moment angulaire implique que 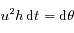 , ainsi
, ainsi 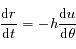 ;
que l'on peut aussi noter
;
que l'on peut aussi noter 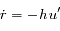 .
De même
.
De même 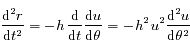 , que l'on peut écrire
, que l'on peut écrire 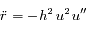
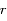 devient:
devient:
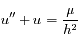
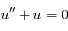 . Le polynôme caractéristique de l'équation est
. Le polynôme caractéristique de l'équation est 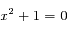 , qui a deux solutions complexes conjuguées
, qui a deux solutions complexes conjuguées  et
et 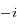 (où
(où  est tel que
est tel que 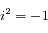 ). Ainsi la solution générale de l'équation sans second membre s'écrit:
). Ainsi la solution générale de l'équation sans second membre s'écrit:
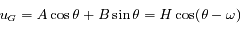
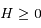 et
et 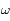 sont des constantes du mouvement dépendant des conditions initiales.
sont des constantes du mouvement dépendant des conditions initiales.
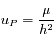 .
On en déduit la solution générale de notre équation:
.
On en déduit la solution générale de notre équation:
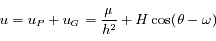
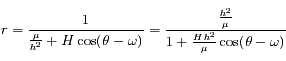
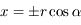
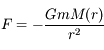 , où
, où 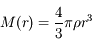 est la masse contenue à l'intérieur de la sphère de rayon
est la masse contenue à l'intérieur de la sphère de rayon 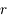 .
.
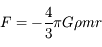 .
.
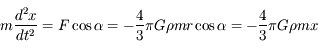 .
.
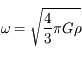 .
.
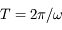 .
.
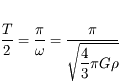 = 42 min 14 s, quels que soient les points A et B.
= 42 min 14 s, quels que soient les points A et B.
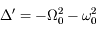
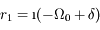 et
et 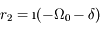 où
où 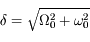 . La solution générale de l'équation différentielle est donc
. La solution générale de l'équation différentielle est donc 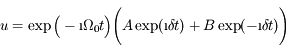
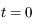 on a
on a 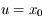 . De plus
. De plus 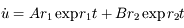 . On en déduit, la vitesse initiale étant nulle, que
. On en déduit, la vitesse initiale étant nulle, que 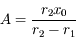 et
et 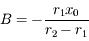 . Donc
. Donc 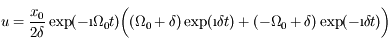
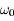 et à
et à 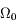 sont de 16,4 s et 31h40min.
sont de 16,4 s et 31h40min.
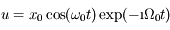
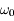 dont le plan d'oscillation tourne avec la fréquence
dont le plan d'oscillation tourne avec la fréquence 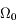 .
.