

Pendule et équation de Mathieu |
Auteur: Alain Vienne
Beaucoup de modèles dynamiques, après maintes transformations (hypothèses simplificatrices, moyennisations, ...), ressemblent au modèle du pendule (masse à une distance constante d'un point fixe sous l'effet de la pesanteur). Ici nous allons nous intéresser à un type d'équation du pendule correspondant à l'équation de Mathieu:
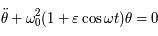
Si 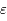 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 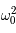 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 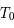 est alors
est alors 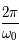 .
.
Ici 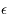 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
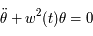
où 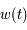 est une fonction périodique de période
est une fonction périodique de période 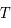 qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
De manière plus ludique, ces équations peuvent modéliser le mouvement d'une balançoire dont le passager se lève et s'assied (périodiquement) afin de s'élancer. Le fait de se lever et de s'assoir régulièrement revient à déplacer le centre de gravité du passager et donc, revient à faire varier périodiquement la longueur du pendule (ici la balançoire).
L'exercice qui suit ne résoud pas l'équation différentielle. Il cherche simplement à savoir dans quelles conditions la solution est bornée ou non (problème de stabilité). Il est insipré du théorème de Gustave Floquet (1847-1920).