Ex: equation de Kepler

Question 1)

On considère le mouvement d'un corps ponctuel 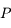de masse négligeable soumise à l'attraction universelle d'un corps de masse 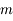situé au centre 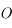du repère de référence. La force s'appliquant à 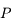est donnée par : 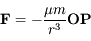$\mathbf{F}=-\frac{\mu m}{r^3}\mathbf{OP}$ , où la notation en gras dénote des vecteurs, 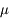$\mu$ est la constante universelle de la gravitation, et 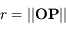$r=||\mathbf{OP}||$ . Les coordonnées de 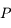dans le repère tournant étant 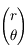${r \choose \theta}$ , on a vu dans l'exercice du problème de 2 corps que la solution des équations du mouvement est :

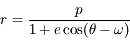$r=\frac{p}{1+e\cos (\theta -\omega)}$ ,

où 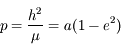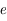$p=\frac{h^2}{\mu}=a(1-e^2)$ , est l'excentricité de la trajectoire, 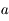est le demi-grand axe et 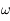$\omega$ est l'argument du péricentre

On a vu aussi que la norme du moment angulaire 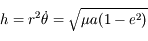$h=r^2\dot{\theta}=\sqrt{\mu a (1-e^2)}$ est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par 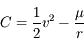$C=\frac{1}{2}v^2-\frac{\mu}{r}$ , où 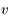est la norme de la vitesse de .

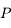Dans le repère tournant on a vu que 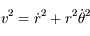$v^2=\dot{r}^2+r^2\dot{\theta}^2$ .

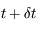Entre un instant et l'instant $t+\delta t$ , le point 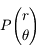$P{r \choose \theta}$ s'est déplacé au point 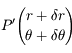$P' {r+\delta r \choose \theta+\delta \theta }$ . En déduire, l'aire élémentaire 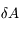$\delta A$ balayée par le rayon vecteur 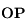$\mathbf{OP}$ pendant l'intervalle de temps 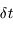$\delta t$ . On ne retiendra que les quantités d'ordre 1.

Solution

Question 2)

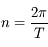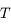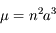En déduire que le mouvement moyen $n=\frac{2\pi}{T}$ , où est la période du mouvement est tel que $\mu=n^2 a^3$ .

Cette relation correspond à la troisième loi de Kepler.

Aide Solution

Question 3)

Après avoir vérifier que 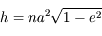$h=na^2\sqrt{1-e^2}$ , montrer que:

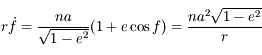
$r\dot{f}=\frac{na}{\sqrt{1-e^2}}(1+e\cos f)=\frac{na^2\sqrt{1-e^2}}{r}$

et que:

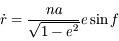
$\dot{r}=\frac{na}{\sqrt{1-e^2}}e\sin f$

où 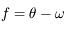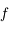$f=\theta-\omega$ . s'appelle l'anomalie vraie et correspond à l'angle entre le péricentre et 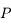vu depuis le foyer .

Solution

Question 4)

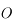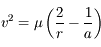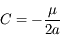Après avoir montrer que $v^2=\mu\left(\frac{2}{r}-\frac{1}{a}\right)$ , en déduire que l'intégrale de l'énergie $C=-\frac{\mu}{2a}$ .

Solution

Question 5)

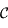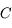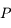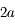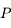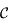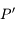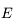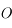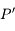Soit $\mathcal{C}$ le cercle de centre le centre de l'ellipse correspondant à la trajectoire de et de diamètre le grand axe de l'ellipse, c'est à dire . La projection de sur le cercle $\mathcal{C}$ parallèlement au petit axe de l'ellipse est noté . On appelle anomalie excentrique l'angle entre et vu depuis 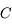. Sachant que l'équation de l'ellipse correspondant à la trajectoire de 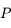dans le repère centré sur 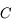et d'axe des abscisses le grand axe dirigé vers le foyer 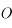, et d'axe des ordonnées la direction orthogonale dans le sens direct, est:

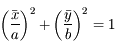$\left(\frac{\bar{x}}{a}\right)^2+\left(\frac{\bar{y}}{b}\right)^2=1$ ,

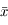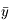en déduire l'expression de $\bar{x}$ et $\bar{y}$ en fonction de 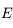, puis l'expression de 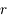en fonction de .

Solution

Question 6)

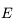Montrer, en utilisant l'expression de 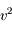v^2 que 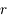vérifie l'équation différentielle suivante:

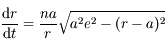
$\frac{\mathrm d r}{\mathrm d t}=\frac{na}{r}\sqrt{a^2e^2-(r-a)^2}$

Solution

Question 7)

En déduire que l'anomalie excentrique vérifie l'équation différentielle:

$\frac{\mathrm d E}{\mathrm dt}=\frac{n}{1-e\cos E}$ .

Aide Solution

Question 8)

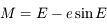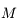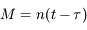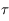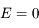En déduire l'équation de Kepler $M=E-e\sin E$ , où l'anomalie moyenne est définie par $M=n(t-\tau)$ où $\tau$ correspond à l'instant de passage au péricentre, c'est à dire quand E=0 .

Solution

Ex: equation de Kepler

équation de Kepler

Equation de Kepler :