Auteur: Stéphane Erard

 Atmosphère planétaire en visible
Atmosphère planétaire en visible
Difficulté : ☆
Temps : 15 min
Question 1)
On se place dans l'approximation "plan-parallèle" où on néglige localement la courbure de la planète. Déterminer l'expression de l'intensité lumineuse reçue à la surface de la Terre ou de Mars, dans le cas où le Soleil est au zénith.
figure 1
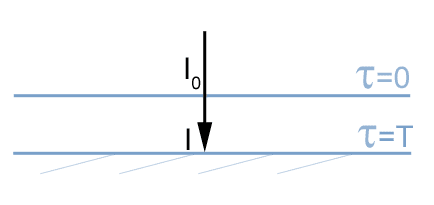
On s'intéresse au flux descendant, le Soleil étant à la verticale.
AideSolution
Ces deux planètes ont une atmosphère fine et sont suffisamment froides pour ne pas émettre en visible. Le terme de source est donc nul, et l'atmosphère ne fait qu'absorber (ou diffuser) la lumière incidente.
Soit 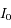 l'intensité reçue au sommet de l'atmosphère (flux solaire).
l'intensité reçue au sommet de l'atmosphère (flux solaire).
Avec les hypothèses ci-dessus, l'équation de transfert s'écrit comme une équation différentielle de premier ordre sans second membre :
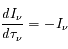 soit :
soit : 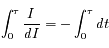
On trouve 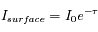
Question 2)
Cas où le Soleil est vu sous un certain angle (la profondeur optique est toujours mesurée à la verticale).
figure 2
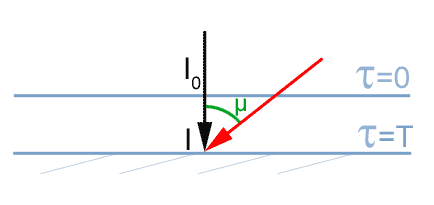
Le Soleil est cette fois vu sous un certain angle.
Solution
Si le Soleil n'est pas au zénith, le problème est identique mais le chemin parcouru dans l'atmosphère est plus long d'un facteur 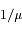 , où
, où 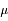 est le cosinus de l'angle d'incidence.
est le cosinus de l'angle d'incidence.
La solution est alors : 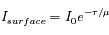
On voit que l'absorption totale augmente quand le Soleil est plus bas sur l'horizon.
Cette loi d'absorption/diffusion très élémentaire est appelée loi de Beer-Lambert.
Auteur: Stéphane Erard

 Face nuit de Vénus
Face nuit de Vénus
Difficulté : ☆☆
Temps : 30 min
Question 1)
Vénus a une température de surface très élevée, de l'ordre de 740 K, qui ne varie quasiment pas au cours de la journée. La température diminue avec l'altitude, pour s'établir à environ 230 K au sommet des nuages côté nuit.
Quelle est l'allure du spectre infrarouge de la face nuit de Vénus ?
figure 3
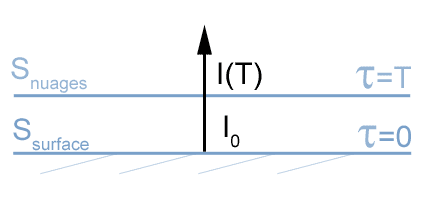
On s'intéresse cette fois au flux montant, qu'on mesure au sommet de l'atmosphère.
Solution
Question 2)
A quoi est due la température de surface ?
Solution
La température très élevée de la surface résulte de la très grande épaisseur optique de l'atmosphère en infrarouge. Celle-ci bloque le rayonnement sortant, et empêche le refroidissement de la surface et des basses couches atmosphériques. Cette opacité est due essentiellement à la diffusion par les goutelettes d'acide sulfurique contenues dans les nuages de haute altitude, et dans une moindre mesure au gaz carbonique et à la vapeur d'eau contenus dans l'atmosphère très dense. Vénus présente un exemple extrême d'effet de serre.
Question 3)
Il existe néanmoins d'étroites régions spectrales entre 1 et 2,5 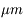 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
Solution
Dans ce cas, il faut résoudre l'équation différentielle avec second membre. En faisant l'hypothèse que le seul terme de source non-négligeable est le corps noir de la surface, on trouve :
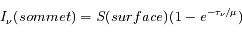
Cette dernière hypothèse est un peu forte, il faudrait en fait tenir compte de l'émisson thermique à toutes les altitudes : la température et l'opacité varient avec l'altitude, et chaque couche de l'atmosphère contribue avec une température différente, qui est atténuée par toute la colonne d'atmosphère au-dessus de cette altitude.
Question 4)
La figure 4 donne un spectre observé de la face nuit de Vénus. Interpréter le flux spectral mesuré à la lumière des questions précédentes.
figure 4
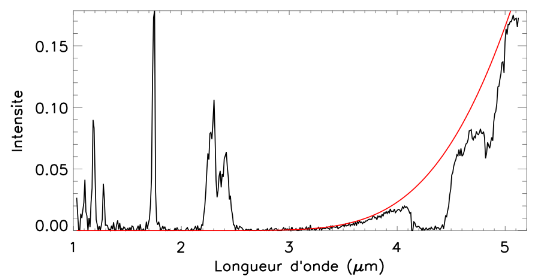
Spectre infrarouge de Vénus mesuré sur la face nuit (instrument Virtis /
Venus-Express). La courbe rouge est un corps noir à 233 K.
Crédit :
ESA / LESIA
Solution





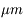 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
