Le transfert de rayonnement décrit l'interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d'analyser la propagation de la lumière à travers un milieu gazeux et joue donc un rôle fondamental dans l'analyse des spectres stellaires et des atmosphères planétaires.
L'équation de transfert fait le bilan énergétique relatif au transport de photons dans un milieu. Comme toujours, on écrit que la quantité à laquelle on s'intéresse varie proportionnellement à sa valeur sur un intervalle suffisamment petit pour que le coefficient soit constant :
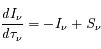
où 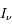 est l'intensité lumineuse à la fréquence
est l'intensité lumineuse à la fréquence 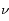 ,
, 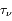 est la profondeur optique du milieu,
est la profondeur optique du milieu, 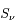 est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
En intégrant cette équation le long du trajet du faisceau lumineux, on a :
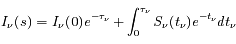
où 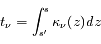 est l'épaisseur optique entre les points s' et s, et
est l'épaisseur optique entre les points s' et s, et 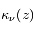 est le coefficient d'absorption du milieu en z.
est le coefficient d'absorption du milieu en z.
On veut résoudre cette équation pour connaître l'intensité en fonction des propriétés du milieu. Les exercices suivants étudient des situations particulières qu'on rencontre fréquemment.
Auteur: Stéphane Erard
 Atmosphère planétaire en visible
Atmosphère planétaire en visible
Difficulté : ☆
Temps : 15 min
Question 1)
On se place dans l'approximation "plan-parallèle" où on néglige localement la courbure de la planète. Déterminer l'expression de l'intensité lumineuse reçue à la surface de la Terre ou de Mars, dans le cas où le Soleil est au zénith.
figure 1
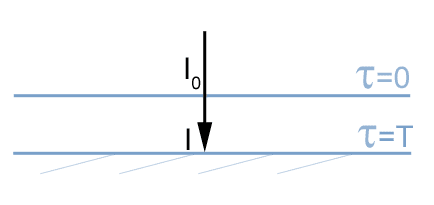
On s'intéresse au flux descendant, le Soleil étant à la verticale.
Ces deux planètes ont une atmosphère fine et sont suffisamment froides pour ne pas émettre en visible. Le terme de source est donc nul, et l'atmosphère ne fait qu'absorber (ou diffuser) la lumière incidente.
Question 2)
Cas où le Soleil est vu sous un certain angle (la profondeur optique est toujours mesurée à la verticale).
figure 2
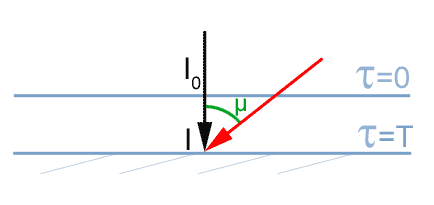
Le Soleil est cette fois vu sous un certain angle.
Auteur: Stéphane Erard
 Face nuit de Vénus
Face nuit de Vénus
Difficulté : ☆☆
Temps : 30 min
Question 1)
Vénus a une température de surface très élevée, de l'ordre de 740 K, qui ne varie quasiment pas au cours de la journée. La température diminue avec l'altitude, pour s'établir à environ 230 K au sommet des nuages côté nuit.
Quelle est l'allure du spectre infrarouge de la face nuit de Vénus ?
figure 3
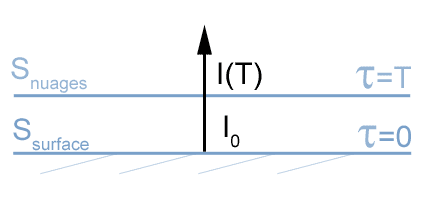
On s'intéresse cette fois au flux montant, qu'on mesure au sommet de l'atmosphère.
Question 2)
A quoi est due la température de surface ?
Question 3)
Il existe néanmoins d'étroites régions spectrales entre 1 et 2,5 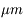 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
Question 4)
La figure 4 donne un spectre observé de la face nuit de Vénus. Interpréter le flux spectral mesuré à la lumière des questions précédentes.
figure 4
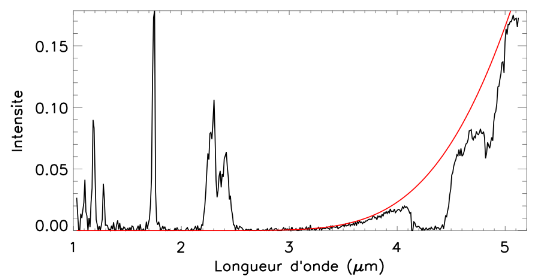
Spectre infrarouge de Vénus mesuré sur la face nuit (instrument Virtis /
Venus-Express). La courbe rouge est un corps noir à 233 K.
Crédit :
ESA / LESIA
Auteur: Marc fouchard
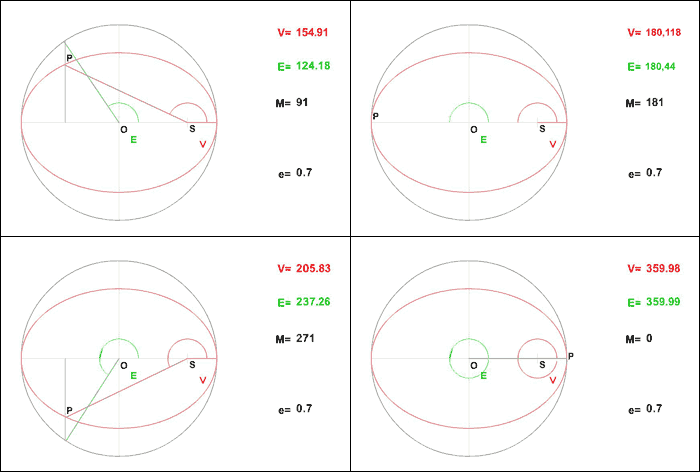
On reprend les résultats obtenus dans l'exercice sur la résolution du problème de 2 corps. Le but est d'obtenir à partir de ces résultats l'équation de Kepler. Cette équation est fondamentale en mécanique céleste puisque c'est elle qui fait le lien entre le temps et la position de l'objet sur son orbite (voir la figure).
Les trois anomalies
 équation de Kepler
équation de Kepler
Difficulté : ☆☆☆
Temps : 1h
Question 1)
On considère le mouvement d'un corps ponctuel  de masse négligeable soumise à l'attraction universelle d'un corps de masse
de masse négligeable soumise à l'attraction universelle d'un corps de masse  situé au centre
situé au centre 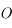 du repère de référence. La force s'appliquant à
du repère de référence. La force s'appliquant à 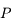 est donnée par :
est donnée par : 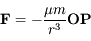 , où la notation en gras dénote des vecteurs,
, où la notation en gras dénote des vecteurs, 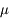 est la constante universelle de la gravitation, et
est la constante universelle de la gravitation, et 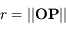 . Les coordonnées de
. Les coordonnées de  dans le repère tournant étant
dans le repère tournant étant 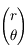 , on a vu dans l'exercice du problème de 2 corps que la solution des équations du mouvement est :
, on a vu dans l'exercice du problème de 2 corps que la solution des équations du mouvement est :
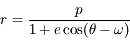 ,
,
où 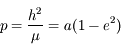 ,
, 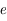 est l'excentricité de la trajectoire,
est l'excentricité de la trajectoire, 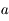 est le demi-grand axe et
est le demi-grand axe et 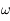 est l'argument du péricentre
est l'argument du péricentre
On a vu aussi que la norme du moment angulaire 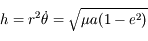 est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par
est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par 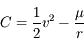 , où
, où 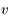 est la norme de la vitesse de
est la norme de la vitesse de  .
.
Dans le repère tournant on a vu que 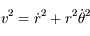 .
.
Entre un instant  et l'instant
et l'instant 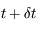 , le point
, le point 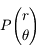 s'est déplacé au point
s'est déplacé au point 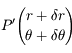 . En déduire, l'aire élémentaire
. En déduire, l'aire élémentaire 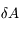 balayée par le rayon vecteur
balayée par le rayon vecteur 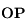 pendant l'intervalle de temps
pendant l'intervalle de temps 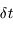 . On ne retiendra que les quantités d'ordre 1.
. On ne retiendra que les quantités d'ordre 1.
Question 2)
En déduire que le mouvement moyen 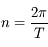 , où
, où 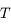 est la période du mouvement est tel que
est la période du mouvement est tel que 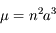 .
.
Cette relation correspond à la troisième loi de Kepler.
Question 3)
Après avoir vérifier que 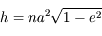 , montrer que:
, montrer que:
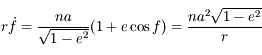
et que:
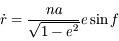
où 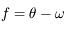 .
. 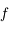 s'appelle l'anomalie vraie et correspond à l'angle entre le péricentre et
s'appelle l'anomalie vraie et correspond à l'angle entre le péricentre et  vu depuis le foyer
vu depuis le foyer 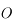 .
.
Question 4)
Après avoir montrer que 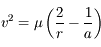 , en déduire que l'intégrale de l'énergie
, en déduire que l'intégrale de l'énergie 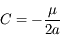 .
.
Question 6)
Montrer, en utilisant l'expression de 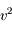 que
que 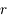 vérifie l'équation différentielle suivante:
vérifie l'équation différentielle suivante:
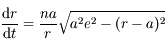
Question 7)
En déduire que l'anomalie excentrique 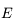 vérifie l'équation différentielle:
vérifie l'équation différentielle:
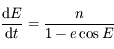 .
.
On part de 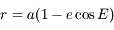 , et on utilise la relation
, et on utilise la relation 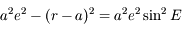 .
.
-
Question 1
Solution :
La surface comme les nuages émettent en première approximation un spectre de corps noir, dont le maximum est donné par la loi de déplacement de Wien, 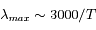 , soit environ 4
, soit environ 4  pour la surface, et 12
pour la surface, et 12 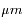 pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du corps noir).
pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du corps noir).
Cependant l'atmosphère de Vénus est extrêmement absorbante dans la plus grande partie du spectre, on a donc 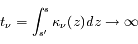 (cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
(cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
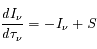 soit
soit 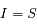 au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La température de brillance (correspondant à l'émission thermique) de la face nuit de Vénus est donc de 230 K, dans la plus grande partie du spectre.
au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La température de brillance (correspondant à l'émission thermique) de la face nuit de Vénus est donc de 230 K, dans la plus grande partie du spectre.
-
Question 2
Solution :
La température très élevée de la surface résulte de la très grande épaisseur optique de l'atmosphère en infrarouge. Celle-ci bloque le rayonnement sortant, et empêche le refroidissement de la surface et des basses couches atmosphériques. Cette opacité est due essentiellement à la diffusion par les goutelettes d'acide sulfurique contenues dans les nuages de haute altitude, et dans une moindre mesure au gaz carbonique et à la vapeur d'eau contenus dans l'atmosphère très dense. Vénus présente un exemple extrême d'effet de serre.
-
Question 3
Solution :
Dans ce cas, il faut résoudre l'équation différentielle avec second membre. En faisant l'hypothèse que le seul terme de source non-négligeable est le corps noir de la surface, on trouve :
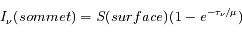
Cette dernière hypothèse est un peu forte, il faudrait en fait tenir compte de l'émisson thermique à toutes les altitudes : la température et l'opacité varient avec l'altitude, et chaque couche de l'atmosphère contribue avec une température différente, qui est atténuée par toute la colonne d'atmosphère au-dessus de cette altitude.
-
Question 4
Solution :
La courbe de corps noir à 233 K ajuste bien la montée de l'intensité à grandes longueurs d'onde, et correspond à l'émission thermique des nuages. Les minima à 4.3 et 4.8 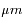 sont des bandes d'absorption du
sont des bandes d'absorption du 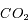 situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
Le flux mesuré est donc beaucoup plus élevé dans les régions optiquement minces. Dans les trois bandes situées autour de 1 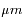 , les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3
, les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3 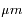 sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
-
Question 1
Solution :
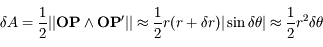 .
.
-
Question 2
Aide :
On rappelle que l'aire totale d'une ellipse est donnée par 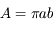 , où
, où 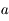 est le demi-grand axe de l'ellipse et
est le demi-grand axe de l'ellipse et 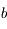 le demi-petit axe donné par
le demi-petit axe donné par 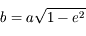 où
où 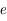 est l'excentricité de l'ellipse.
est l'excentricité de l'ellipse.
Solution :
En passant à la limite dans l'expression précédente on a: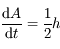 . Or l'aire balayée pendant une période
. Or l'aire balayée pendant une période 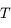 n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
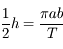 où
où 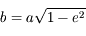 est le demi-petit axe de l'ellipse. Avec
est le demi-petit axe de l'ellipse. Avec 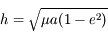 ,
on obtient
,
on obtient 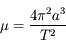 , ce qui correspond bien à la relation demandée.
, ce qui correspond bien à la relation demandée.
-
Question 3
Solution :
Comme 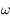 est constant, on a
est constant, on a 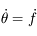 . Ainsi
. Ainsi 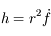 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
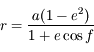 ,
,
Ainsi:
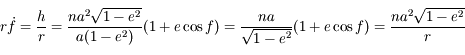 .
.
De même en différentiant l'équation précédente obtenue pour 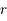 on obtient:
on obtient:
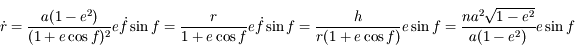 .
.
Ce qui correspond bien à l'équation demandée.
-
Question 4
Solution :
On calcule d'abord 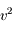 :
:
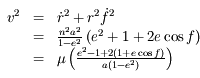 ,
,
qui correspond bien à la relation demandée.
On obtient facilement 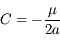 en subsituant
en subsituant 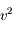 par l'expression ci-dessus dans
par l'expression ci-dessus dans 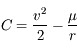 .
.
-
Question 5
Solution :
On a facilement 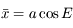 et d'après l'équation de l'ellipse on en déduit
et d'après l'équation de l'ellipse on en déduit 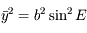 . Comme
. Comme 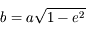 , on en déduit que
, on en déduit que 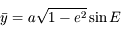 .
.
Ainsi, dans un repère centré sur  avec les mêmes axes on a:
avec les mêmes axes on a: 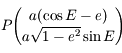 .
.
On en déduit : 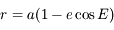 .
.
-
Question 6
Solution :
On a:
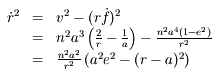 ,
,
ce qui correspond bien à l'équation demandée.
-
Question 7
Aide :
On part de 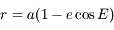 , et on utilise la relation
, et on utilise la relation 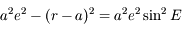 .
.
Solution :
On a vu que 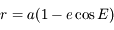 , ainsi
, ainsi 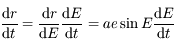 .
.
D'autre part:
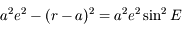 ,
,
Ainsi, on a bien l'équation demandée pour 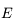 .
.
-
Question 8
Solution :
L'équation différentielle obtenue pour 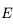 s'écirt:
s'écirt: 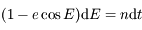 . En intégrant entre l'instant où
. En intégrant entre l'instant où 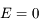 et
et 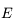 ,on obtient
,on obtient 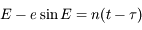 qui correspond bien à l'équation de Kepler.
qui correspond bien à l'équation de Kepler.
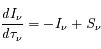
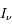 est l'intensité lumineuse à la fréquence
est l'intensité lumineuse à la fréquence 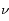 ,
, 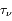 est la profondeur optique du milieu,
est la profondeur optique du milieu, 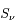 est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
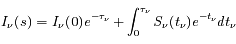
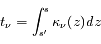 est l'épaisseur optique entre les points s' et s, et
est l'épaisseur optique entre les points s' et s, et 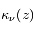 est le coefficient d'absorption du milieu en z.
est le coefficient d'absorption du milieu en z.



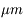 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.


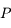 de masse négligeable soumise à l'attraction universelle d'un corps de masse
de masse négligeable soumise à l'attraction universelle d'un corps de masse 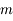 situé au centre
situé au centre 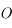 du repère de référence. La force s'appliquant à
du repère de référence. La force s'appliquant à 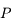 est donnée par :
est donnée par : 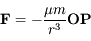 , où la notation en gras dénote des vecteurs,
, où la notation en gras dénote des vecteurs, 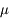 est la constante universelle de la gravitation, et
est la constante universelle de la gravitation, et 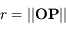 . Les coordonnées de
. Les coordonnées de 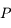 dans le repère tournant étant
dans le repère tournant étant 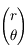 , on a vu dans l'exercice du
, on a vu dans l'exercice du 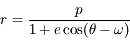 ,
,
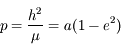 ,
, 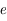 est l'
est l'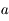 est le
est le 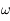 est l'
est l'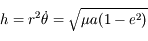 est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par
est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par 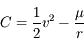 , où
, où 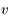 est la norme de la vitesse de
est la norme de la vitesse de 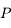 .
.
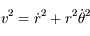 .
.
 et l'instant
et l'instant 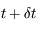 , le point
, le point 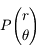 s'est déplacé au point
s'est déplacé au point 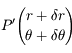 . En déduire, l'aire élémentaire
. En déduire, l'aire élémentaire 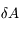 balayée par le rayon vecteur
balayée par le rayon vecteur 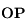 pendant l'intervalle de temps
pendant l'intervalle de temps 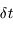 . On ne retiendra que les quantités d'ordre 1.
. On ne retiendra que les quantités d'ordre 1.
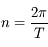 , où
, où 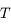 est la période du mouvement est tel que
est la période du mouvement est tel que 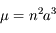 .
.
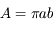 , où
, où 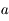 est le demi-grand axe de l'ellipse et
est le demi-grand axe de l'ellipse et 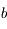 le demi-petit axe donné par
le demi-petit axe donné par 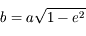 où
où 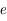 est l'excentricité de l'ellipse.
est l'excentricité de l'ellipse.
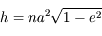 , montrer que:
, montrer que:
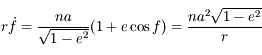
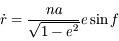
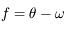 .
. 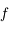 s'appelle l'
s'appelle l' vu depuis le foyer
vu depuis le foyer 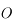 .
.
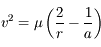 , en déduire que l'intégrale de l'énergie
, en déduire que l'intégrale de l'énergie 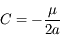 .
.
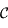 le cercle de centre le centre
le cercle de centre le centre 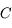 de l'ellipse correspondant à la trajectoire de
de l'ellipse correspondant à la trajectoire de 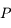 et de diamètre le grand axe de l'ellipse, c'est à dire
et de diamètre le grand axe de l'ellipse, c'est à dire 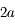 . La projection de
. La projection de 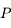 sur le cercle
sur le cercle 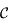 parallèlement au petit axe de l'ellipse est noté
parallèlement au petit axe de l'ellipse est noté 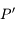 . On appelle
. On appelle 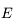 entre
entre 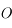 et
et 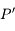 vu depuis
vu depuis 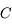 . Sachant que l'équation de l'ellipse correspondant à la trajectoire de
. Sachant que l'équation de l'ellipse correspondant à la trajectoire de 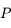 dans le repère centré sur
dans le repère centré sur 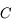 et d'axe des abscisses le grand axe dirigé vers le foyer
et d'axe des abscisses le grand axe dirigé vers le foyer 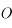 , et d'axe des ordonnées la direction orthogonale dans le sens direct, est:
, et d'axe des ordonnées la direction orthogonale dans le sens direct, est:
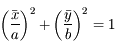 ,
,
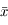 et
et 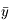 en fonction de
en fonction de 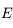 , puis l'expression de
, puis l'expression de 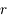 en fonction de
en fonction de 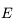 .
.
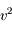 que
que 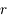 vérifie l'équation différentielle suivante:
vérifie l'équation différentielle suivante:
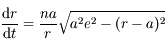
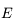 vérifie l'équation différentielle:
vérifie l'équation différentielle:
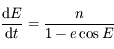 .
.
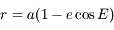 , et on utilise la relation
, et on utilise la relation 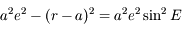 .
.
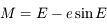 , où l'
, où l'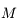 est définie par
est définie par 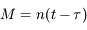 où
où 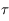 correspond à l'instant de passage au péricentre, c'est à dire quand
correspond à l'instant de passage au péricentre, c'est à dire quand 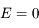 .
.
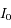 l'intensité reçue au sommet de l'atmosphère (flux solaire).
l'intensité reçue au sommet de l'atmosphère (flux solaire).
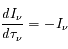 soit :
soit : 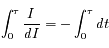
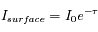
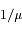 , où
, où 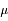 est le cosinus de l'angle d'incidence.
est le cosinus de l'angle d'incidence.
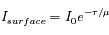
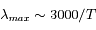 , soit environ 4
, soit environ 4 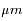 pour la surface, et 12
pour la surface, et 12 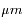 pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du
pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du 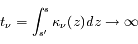 (cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
(cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
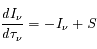 soit
soit 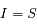 au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La
au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La 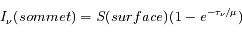
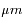 sont des bandes d'absorption du
sont des bandes d'absorption du 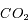 situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
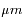 , les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3
, les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3 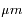 sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
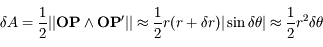 .
.
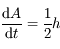 . Or l'aire balayée pendant une période
. Or l'aire balayée pendant une période 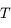 n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
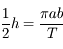 où
où 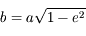 est le demi-petit axe de l'ellipse. Avec
est le demi-petit axe de l'ellipse. Avec 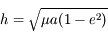 ,
on obtient
,
on obtient 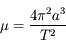 , ce qui correspond bien à la relation demandée.
, ce qui correspond bien à la relation demandée.
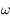 est constant, on a
est constant, on a 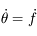 . Ainsi
. Ainsi 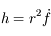 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
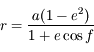 ,
,
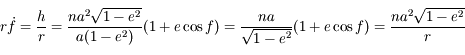 .
.
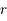 on obtient:
on obtient:
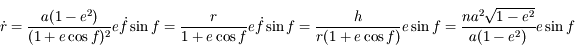 .
.
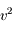 :
:
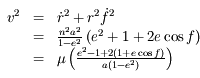 ,
,
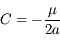 en subsituant
en subsituant 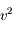 par l'expression ci-dessus dans
par l'expression ci-dessus dans 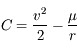 .
.
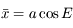 et d'après l'équation de l'ellipse on en déduit
et d'après l'équation de l'ellipse on en déduit 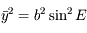 . Comme
. Comme 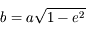 , on en déduit que
, on en déduit que 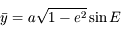 .
.
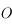 avec les mêmes axes on a:
avec les mêmes axes on a: 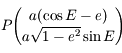 .
.
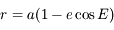 .
.
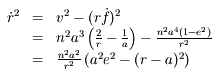 ,
,
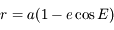 , ainsi
, ainsi 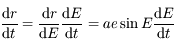 .
.
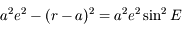 ,
,
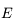 .
.
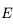 s'écirt:
s'écirt: 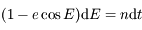 . En intégrant entre l'instant où
. En intégrant entre l'instant où  et
et  ,on obtient
,on obtient 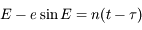 qui correspond bien à l'équation de Kepler.
qui correspond bien à l'équation de Kepler.
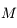 connaissant
connaissant 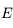 . Malheureusement on a en générale besoin de connaître
. Malheureusement on a en générale besoin de connaître 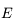 (qui est un angle géométrique relié à la position de l'objet sur son orbite) connaissant
(qui est un angle géométrique relié à la position de l'objet sur son orbite) connaissant 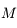 (qui est proportionelle au temps). Pour cela on doit inverser l'équation de Kepler. Cette inversion est l'objet de cet
(qui est proportionelle au temps). Pour cela on doit inverser l'équation de Kepler. Cette inversion est l'objet de cet