

Longueur de Debye |
Auteur: Arnaud Beck
Un plasma est une collection de particules chargées. Pour simplifier, considérons qu'il n'est composé que d'électrons de charge 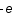 et d'ions de charge
et d'ions de charge 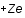 .
.
Un ion, considéré comme ponctuel, lorsqu'il est dans le vide crée autour de lui un potentiel 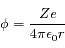 où
où 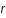 est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
Dans un plasma, il en va différemment. En effet, il va attirer autour de lui des charges de signe opposé (les électrons) qui vont écranter son potentiel. La sphère d'électrons qui se forme autour de l'ion est appelée la sphère de Debye et son rayon est appelé la longueur de Debye. C'est un paramètre fondamental en physique des plasmas.
Dans cet exercice, on propose de retrouver la valeur de ce rayon et la forme du potentiel à l'intérieur de la sphère de Debye.