

Ex: Pendule de Foucault |
Difficulté : ☆☆ Temps : 1h
Le but de cet exercice est de reprendre la modélisation du pendule en tenant compte du fait que le repère terrestre n'est pas galiléen, mais est animé d'un mouvement de rotation de la Terre elle-même. La véritable motivation de l'exercice est la résolution de l'équation différentielle du mouvement.
On considère un pendule constitué d'un fil 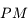 accroché en
accroché en 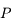 de longueur
de longueur 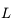 et d'une boule
et d'une boule 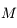 de masse
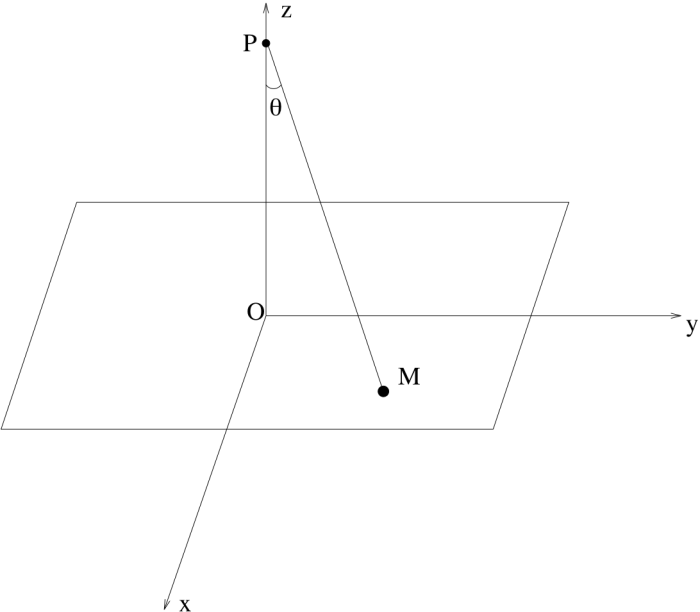
de masse 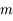 . L'espace est rapporté au système d'axes
. L'espace est rapporté au système d'axes 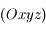 fixe dans le réferentiel lié à la Terre, l'axe
fixe dans le réferentiel lié à la Terre, l'axe 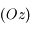 passant par
passant par 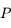 et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule
et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule 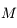 de coordonnées
de coordonnées 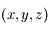 se fait dans le plan
se fait dans le plan 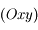 et que le module de la tension du fil
et que le module de la tension du fil 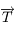 est
est 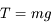 où
où 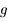 est l'accélération de la pesanteur. On note
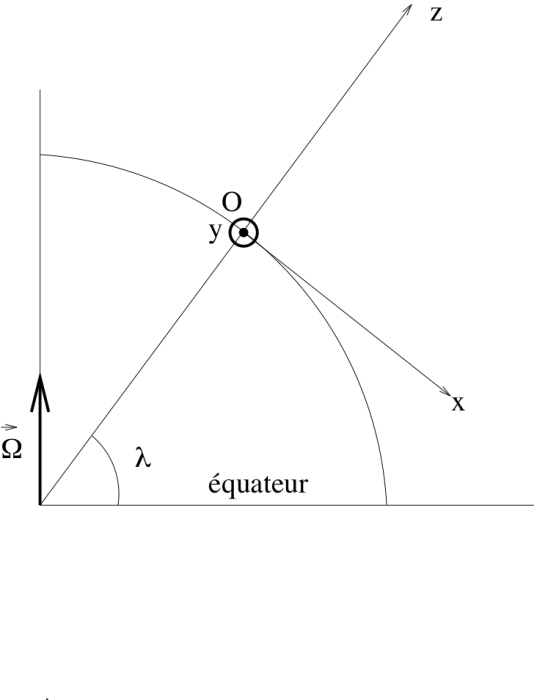
est l'accélération de la pesanteur. On note 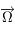 le vecteur rotation de la Terre et
le vecteur rotation de la Terre et 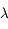 la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est
la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est 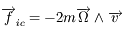 où
où 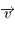 désigne la vitesse dans le repère
désigne la vitesse dans le repère 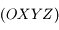 . Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de
. Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de 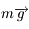 .
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans
.
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans 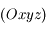 sont
sont 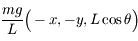 et que les composantes de la force de Coriolis sont
et que les composantes de la force de Coriolis sont 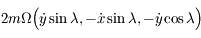 . D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur
. D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur 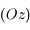 , celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant
, celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant 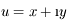 où
où 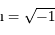 , et en posant aussi
, et en posant aussi 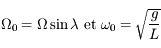 on peut montrer que l'équation du mouvement, complexe, se met sous la forme :
on peut montrer que l'équation du mouvement, complexe, se met sous la forme : 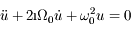 .
.
L'équation différentielle du mouvement qu'on se propose de résoudre est :
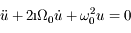
Ecrire le discriminant réduit de cette équation.
Déterminer les solutions de l'équation caractéristiques, et en déduire la forme générale de la solution de l'équation différentielle.
Particulariser la solution précédente en considérant qu'à l'instant initial, le mobile se trouve en 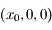 avec une vitesse initiale nulle.
avec une vitesse initiale nulle.
Dans les conditions de l'expérience de Foucault faite au Panthéon en 1851, on a les valeurs suivantes: 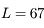 m,
m, 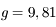 m/s2, et
m/s2, et 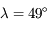 Nord. Justifier que
Nord. Justifier que 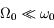 .
.
Simplifier l'expression de la solution trouvée en négligeant 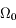 devant
devant 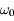 . Interpréter.
. Interpréter.