

Ex: Train gravitationnel |
Difficulté : ☆ Temps : 1h
On assimile la Terre à une sphère sans rotation de rayon 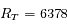 km et de masse volumique uniforme
km et de masse volumique uniforme 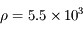
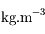 . Soit
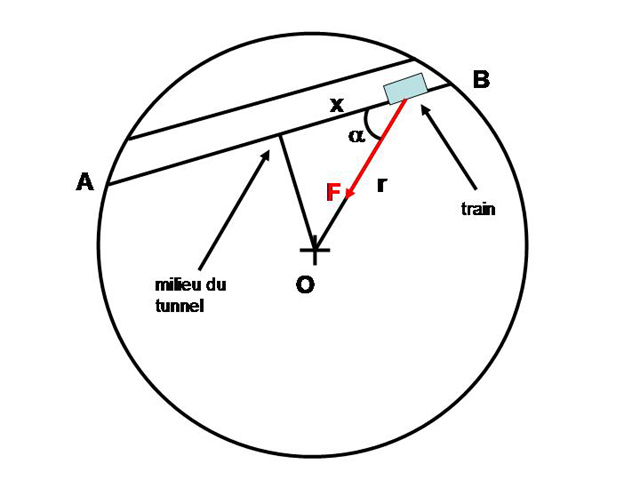
. Soit 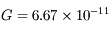 S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
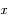 , sa distance au centre de la Terre est notée
, sa distance au centre de la Terre est notée 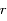 .
.
Soit 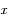 la distance du train au milieu du tunnel. Exprimer
la distance du train au milieu du tunnel. Exprimer 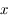 en fonction de la distance au centre de la Terre
en fonction de la distance au centre de la Terre 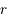 et de l'angle
et de l'angle 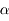 .
.
Donner l'expression de la force gravitationnelle 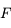 agissant sur le train en fonction de la masse du train
agissant sur le train en fonction de la masse du train 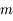 , de la masse volumique de la Terre
, de la masse volumique de la Terre 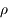 et de la distance au centre de la Terre
et de la distance au centre de la Terre 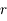 .
.
En déduire l'équation du mouvement du train dans le tunnel.
Le train peut-il atteindre le point B, et si oui, en combien de temps?