Auteur: Stéphane Erard
L'arithmétique intervient en Astronomie lorsqu'il est question de phénomènes périodiques. Historiquement, la prévision des éclipses et des fêtes religieuses a fait appel à de tels calculs. Dans la période moderne, c'est la mécanique quantique (à travers l'équation de Schrödinger) qui introduit des solutions à base de nombres entiers.
Auteur: Stéphane Erard
 Phénomènes mutuels
Phénomènes mutuels
Difficulté : ☆☆
Temps : 45 min
Le corps céleste A a une période synodique (par rapport à la Terre) de 105 jours et passe à l'opposition à la date 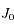 . Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
. Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
On veut déterminer la date 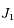 de la prochaine opposition simultanée des deux corps.
de la prochaine opposition simultanée des deux corps.
Question 1)
Trouver une condition permettant de déterminer cette date.
Question 2)
Trouver une solution particulière de cette équation.
Question 3)
Déterminer toutes les solutions de l'équation trouvée plus haut.
Question 4)
Quelle est la date de la prochaine opposition commune ?
Question 5)
Application à Mars et Jupiter : une opposition de Mars a eu lieu le 24/12/2007, l'opposition suivante de Jupiter le 4/7/2008. Les périodes synodiques respectives sont de 780 et 399 jours. Quand se produira la prochaine opposition simultanée des deux planètes ?
L'intervalle entre les deux oppositions est de 193 jours (on calcule ce type d'intervalle en convertissant les dates en jours juliens, ce que font tous les tableurs courants).
Auteur: Stéphane Erard
Les premières mesures spectroscopiques ont révélé à la fin du XIXe siècle un comportement inattendu des sources lumineuses : elles présentent fréquemment des raies intenses, soit en absorption soit en émission. Pour une source donnée, l'émission ou l'absorption ne se produisent qu'à certaines longueurs d'onde. La formule expérimentale de Balmer-Rydberg (1885-88) rend compte de la position de ces raies pour l'atome d'hydrogène, mais ne correspond à aucun phénomène connu.
Divers modèles de structure atomique ont été proposés dans les années suivantes pour intégrer les résultats expérimentaux de l'époque. Le modèle de Bohr pour l'atome d'hydrogène (1913) a fourni la première explication des résultats spectroscopiques. Il implique un comportement non-classique des systèmes microscopiques, qui sautent sans transition entre états d'énergie discrets.
Auteur: Stéphane Erard
 Modèle de Rutherford
Modèle de Rutherford
Difficulté : ☆
Temps : 30 min
Un des premiers modèles atomiques modernes est celui de Rutherford (1911), s'appuyant sur des expériences de diffusion de particules alpha. Ce modèle suppose que l'atome est formé d'un noyau de très petites dimensions chargé positivement, autour duquel gravitent des électrons négatifs beaucoup moins massifs sur des orbites circulaires. En raison d'une analogie évidente, on l'appelle modèle planétaire.
Question 1)
On considère un atome d'hydrogène où un électron unique orbite autour d'un noyau de charge unité. L'électron est soumis à une force électrostatique d'intensité 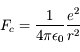
où e est la charge de l'électron et du noyau (opposées), r leur distance et 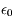 une constante physique (permittivité du vide).
une constante physique (permittivité du vide).
Ecrire la distance électron-noyau dans ce modèle.
On écrit le principe fondamental de la dynamique 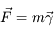 et on projette sur le rayon vecteur.
et on projette sur le rayon vecteur.
Question 2)
Calculer l'énergie totale (cinétique et potentielle).
Auteur: Stéphane Erard
 Atome de Bohr
Atome de Bohr
Difficulté : ☆
Temps : 45 min
Une difficulté avec le modèle de Rutherford est qu'il ne rend pas compte des expériences de spectroscopie de l'époque et de l'existence de raies spectrales. Par ailleurs, l'électrodynamique classique prévoit que les électrons devraient rayonner et perdre de l'énergie, ce qui les ferait tomber sur le noyau très rapidement.
Niels Borh travaillait à ce problème quand il prit connaissance de la formule de Balmer qui donne la position observée des raies spectrales de l'hydrogène dans le visible :
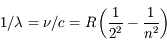
où 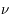 est la fréquence associée, n est un nombre entier > 2, R une constante et c la vitesse de la lumière.
est la fréquence associée, n est un nombre entier > 2, R une constante et c la vitesse de la lumière.
Par ailleurs il connaissait l'hypothèse d'Einstein formulée pour l'étude de l'effet photo-électrique : la lumière peut se décomposer en "quanta" (les photons) dont l'énergie est liée à la fréquence 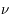 du rayonnement :
du rayonnement : 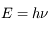 .
.
En rapprochant ces faits, Bohr formula l'hypothèse que l'atome ne peut prendre que certains états d'énergie donnés dans son modèle atomique (1913).
Question 1)
Calculer les longueurs d'onde des raies visibles et dessiner le spectre de l'hydrogène à l'aide de la formule ci-dessus. On prendra les raies de Balmer n = 3 à 6 qui sont dans le domaine visible, et 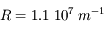 (constante de Rydberg).
(constante de Rydberg).
Question 2)
Ecrire les variations d'énergie de l'atome d'hydrogène liées à l'émission d'une raie de la série de Balmer.
Question 3)
En déduire les valeurs possibles du rayon de l'électron et du moment cinétique 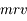 .
.
Question 4)
Comment interpréter ce résultat ?
 remarque
remarque
Les autres séries de raies de l'hydrogène correspondent à des transitions vers les couches n ≠ 2. On peut représenter les niveaux énergétiques de l'hydrogène de la façon suivante :
Diagramme énergétique de l'hydrogène
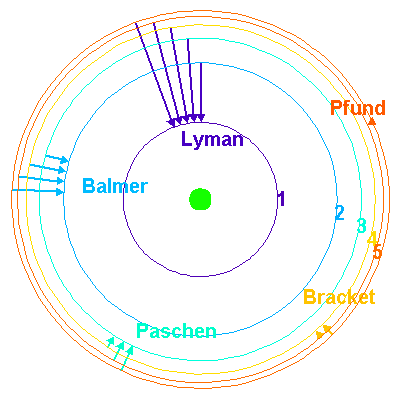
La première raie de Balmer 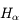 est particulièrement importante en Astronomie car elle permet de détecter l'hydrogène atomique dans le milieu interstellaire.
est particulièrement importante en Astronomie car elle permet de détecter l'hydrogène atomique dans le milieu interstellaire.
Auteur: Alexandre Pousse
Introduction
Les fractions continues ont une très longue histoire car liées à celle des nombres. En effet, il existe un lien important entre celles-ci et l'algorithme d'Euclide.
Plus particulièrement, elles apparaissent dans l'approximation de nombre comme π ou du nombre d'or.
Délaissées pendant un certain temps, elles sont redécouvertes en Europe en 1655 par le mathématicien anglais John Wallis, puis étudiées par la suite par Leonhard Euler qui va apporter de nombreux théorèmes.
L'interêt de l'étude des fractions continues est souvent pour l'approximation d'équations diophantiennes. Ce sont des équations algébriques pour lesquelles on cherche des solutions en entiers. Un exemple particulier qui est utile en astronomie car permettant de mettre en évidence des phénomènes de résonnances ou de prévoir le retour d'un phénomène périodique, c'est de fixer 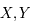 deux nombres représentant des périodes, et de trouver
deux nombres représentant des périodes, et de trouver 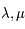 , deux entiers tels que
, deux entiers tels que 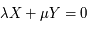 . La notion d'approximation introduite par les fractions continues est utilisée lorsque
. La notion d'approximation introduite par les fractions continues est utilisée lorsque 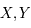 sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant
sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant 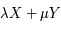 .
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
.
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
Définitions et propriétés
Une fraction continue est un objet s'écrivant sous la forme 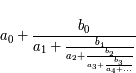 où les
où les 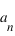 et les
et les 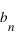 sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
Mais ce que nous utiliserons par la suite et qui ont été étudiées plus particulièrement, ce sont les fractions continues simples, c'est-à-dire de la forme 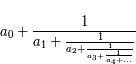 avec
avec 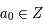 et
et 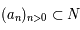 (fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire
(fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire ![[a_0;a_1;a_2;...;a_n;...]](../pages_quotient/equations_quotient/equation57.png) .
.
Afin de caractériser une fraction continue, on utilise la notion de réduite. Par exemple, pour 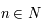 , on appellera réduite de la fraction continue définie par la suite
, on appellera réduite de la fraction continue définie par la suite 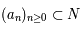 , la fraction
, la fraction ![\frac{p_n}{q_n}=[a_0;a_1;a_2;a_3;...;a_n]](../pages_quotient/equations_quotient/equation60.png) . Pour le nombre d'or
. Pour le nombre d'or 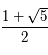 , les trois premières réduites sont
, les trois premières réduites sont ![\frac{p_0}{q_0}= [1]](../pages_quotient/equations_quotient/equation62.png) ,
, ![\frac{p_1}{q_1}=[1;1]](../pages_quotient/equations_quotient/equation63.png) ,
, ![\frac{p_2}{q_2}=[1;1;1]](../pages_quotient/equations_quotient/equation64.png) .
Ainsi, nous obtenons deux suites d'entiers
.
Ainsi, nous obtenons deux suites d'entiers 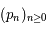 et
et 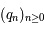 avec en particulier, la propriété suivante:
si
avec en particulier, la propriété suivante:
si 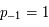 ,
, 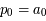 et
et 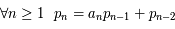 , et si
, et si 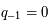 ,
, 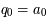 et
et 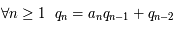 , alors
, alors ![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation73.png) .
.
Approximation des nombres
Introduisons maintenant la fraction continue dans le cadre de l'approximation des nombres. Soit α un réel et 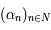 une suite de réels telle que:
une suite de réels telle que:
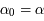 ,
,
si 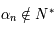 alors
alors 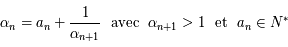 ,
,
sinon 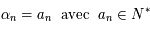 .
.
Ainsi, on obtient le développement suivant ![\alpha = a_0 + \frac{1}{\alpha_1}= a_0 + \frac{1}{a_1 + \frac{1}{\alpha_2}}} = a_0 + \frac{1}{a_1 + \frac{1}{a_2+ \frac{1}{\alpha_3}}}}=...=[a_0;a_1;a_2;...;a_n+ \frac{1}{\alpha_{n+1}}]=...](../pages_quotient/equations_quotient/equation79.png)
Les exercices qui suivent vont ainsi permettre de mettre en évidence la propriété théorique sur les réduites ainsi que des applications astronomique par la recherche de meilleure solution approximation de l'équation diophantienne via les fractions continues en caractérisant le mouvement de Saturne et de la Terre, le phénomène d'éclipse et en définissant une meilleure approximation de l'année tropique.
Auteur: Alexandre Pousse
 Propriété des réduites
Propriété des réduites
Difficulté : ☆
Temps : 10 min
Soient 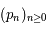 et
et 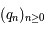 , deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
, deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
si 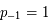 ,
, 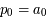 et
et 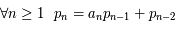 ,
,
et si 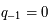 ,
, 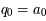 et
et 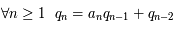 ,
,
alors ![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation93.png) .
.
Question 1)
Démontrer la propriété des réduites.
Auteur: Alexandre Pousse
 Une meilleure approximation de l'année tropique
Une meilleure approximation de l'année tropique
Difficulté : ☆
Temps : 30 min
Une année tropique correspond au temps s'écoulant entre deux équinoxes de printemps, c'est-à-dire 365.24219052 jours (année tropique moyenne à J2000). C'est donc l'année permettant "le retour des saisons" au mêmes dates et donc compensant le phénomène de précession des équinoxes.
En effet, avant la réforme du calendrier par Grégoire XIII au XVIe siècle, le calendrier était le calendrier Julien, établi par l'astronome Sosigène d'Alexandrie et comportant 365.25 jours (année bissextile tous les quatre ans). Cela impliquait un décalage d'un jour tous les 128 ans, d'où modification de la date de retour des saisons.
L'idée de cet exercice est de comprendre le calendrier utilisé aujourd'hui, puis de trouver par l'intermédiaire d'une fraction continue une valeur plus stable de l'année.
Question 1)
L'année grégorienne correspond à 366 jours les années multiples de quatre et non multiples de cent sauf les année multiples de quatre cents. Sinon, l'année vaut 365 jours.
Établir la valeur et la fraction représentant la partie décimale de l'année grégorienne.
Question 2)
On définira la notion de stabilité comme l'écart la durée de l'année estimée et la durée de l'année tropique moyenne. Le réel obtenu permet de déduire le décalage du retour des équinoxes.
Évaluer la stabilité du calendrier grégorien. Au bout de combien de temps le calendrier se décale d'un jour?
Question 3)
En utilisant la méthode d'approximation des nombres à l'aide d'une fraction continue, trouver une nouvelle définition de l'année beaucoup plus stable que l'année grégorienne. Proposer une méthode d'application pour remplacer le calendrier actuel.
Auteur: Alexandre Pousse
 L'automate de Huygens
L'automate de Huygens
Difficulté : ☆
Temps : 30 min
Christian Huygens, mathématicien et astronome du XVIIe siècle, souhaitait réaliser un automate planétaire permettant de modéliser l'évolution du système solaire au cours du temps (en approximation circulaire). À cet époque, le système solaire ne comprend que 6 planètes (Mercure, Venus, Terre, Mars, Jupiter et Saturne). Rappelons qu'un automate est un système composé d'une manivelle reliée à différents rouages, chacun associé à la période de révolution d'une planète par leur nombre de dents.
Lors de la conception de cet objet, Huygens se retrouve confronté à une difficulté: le rapport de l'année terrestre et de celle de Saturne. Combien faut-il de dents sur les deux engrenages pour décrire convenablement le mouvement de la Terre et de Saturne au cours de leur révolution?
Question 1)
Dans l'approximation d'orbites circulaires, poser l'équation diophantienne du problème de l'automate.
Question 2)
Sur son orbite, la Terre parcourt un angle 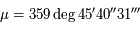 en un an. De même en un an, Saturne réalise
en un an. De même en un an, Saturne réalise 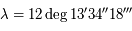 (Ce sont les valeurs de l'époque).
(Ce sont les valeurs de l'époque).
Établir la fraction rationnelle donnée par le rapport 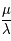 . Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
. Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
Question 3)
Maintenant, afin de supprimer ce problème technique, introduire la notion de fraction continue pour résoudre le problème par approximation diophantienne.
Question 4)
Huygens définit la notion de stabilité comme le décalage entre l'angle parcouru par Saturne sur son automate et dans la réalité après que la Terre ait réalisé 100 révolutions.
À l'aide d'un développement en fraction continue, proposer un engrenage satisfaisant d'un point de vue technique (au delà d'un millier de dents, la réalisation est difficile) et stable au sens de Huygens.
Auteur: Alexandre Pousse
 Le cycle de Saros
Le cycle de Saros
Difficulté : ☆
Temps : 60 min
Un cycle de Saros correspond à 223 lunaisons. C'est une période associée au retour d'une éclipse de Soleil (resp. de Lune) après une éclipse totale. Ainsi, si une éclipse a lieu à un instant t alors il est possible de prédire qu'au temps t+223 lunaisons il s'en reproduira une autre.
L'idée de cet exercice est de comprendre et de retrouver pourquoi nous avons ce nombre de 223 lunaisons pour le retour d'une éclipse.
Question 1)
Définir géométriquement la notion d'éclipse de Lune (resp. de Soleil) vu de la Terre (avec la notion de droite ou de plan par exemple).
Question 2)
Caractériser la notion d'éclipse en terme de position de la Lune sur son orbite ainsi que de son éclairement relatif à la Terre.
Question 3)
Introduisons deux notions pour la détermination de cycle de Saros.
Le mois draconitique, c'est le temps que met la Lune à partir du noeud ascendant pour y revenir. La durée du mois draconitique est de 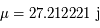 .
.
Le mois synodique ou lunaison est le temps entre deux nouvelles Lunes successives. Sa durée est d'en moyenne 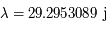 .
.
Dans l'approximation d'orbites circulaires, poser l'équation diophantienne du problème du retour d'éclipse.
Question 4)
Introduire la notion de fraction continue pour résoudre le problème par approximation diophantienne.
Question 5)
Rappelons que le diamètre de la Lune et du Soleil vu de la Terre est de 30' d'arc.
Établir l'erreur de coincidence maximal pour que l'on ait une éclipse (on considère qu'une éclipse partielle est encore une éclipse).
Question 6)
Développer la fraction continue jusqu'au terme adéquat (évaluation des réduites et contrôle de l'erreur de coïncidence).
Question 7)
Conclure sur la notion de cycle de Saros.
Question 8)
Vous vous rappelez peut-être de l'éclipse totale de Soleil du 11 août 1999 (éclipse totale de la Normandie à l'Alsace en France et partielle au voisinage de cette bande). Déterminer quand cette configuration va t-elle se reproduire? Va t-elle avoir lieu aux mêmes longitudes?
-
Question 1
Solution :
Les dates d'opposition du corps A sont 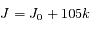 , où k est un nombre entier (relatif).
, où k est un nombre entier (relatif).
Les dates d'opposition du corps B sont 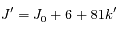 , où k' est un autre nombre entier.
, où k' est un autre nombre entier.
On cherche la première date telle que 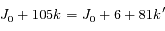 , soit
, soit 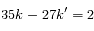 , où k et k' sont les nombres de périodes effectuées par les corps A et B entre
, où k et k' sont les nombres de périodes effectuées par les corps A et B entre 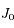 et
et 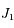 . On reconnaît une équation diophantienne, reliant trois nombres entiers.
. On reconnaît une équation diophantienne, reliant trois nombres entiers.
-
Question 2
Solution :
On commence par chercher une solution particulière de l'équation plus simple 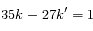 . Le couple (-10, -13) est une telle solution.
. Le couple (-10, -13) est une telle solution.
On aura donc (k,k') = 2(-10,-13) = (-20,-26), solution particulière recherchée.
-
Question 3
Solution :
Les couples solutions (x,y) sont tels que 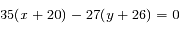 .
.
On cherche y tel que 35 divise 27(y+26), alors que 35 est premier avec 27. Le théorème de Gauss indique que 35 doit être un diviseur entier de y+26, donc qu'il existe un nombre k tel que 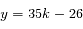
En remplaçant y dans l'équation, on trouve 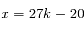 , donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
, donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
-
Question 4
Solution :
Le plus court intervalle correspond à k = 1, soit 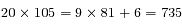 jours.
jours.
-
Question 5
Aide :
L'intervalle entre les deux oppositions est de 193 jours (on calcule ce type d'intervalle en convertissant les dates en jours juliens, ce que font tous les tableurs courants).
Solution :
Le même calcul que précédemment donne
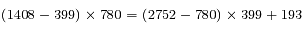 jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.
jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.
-
Question 1
Solution :
Les premières raies de la série de Balmer ont les caractéristiques suivantes :
Série de Balmer
| Niveau de départ |
Niveau d'arrivée |
Nom de la raie |
Longueur d'onde (nm) |
| 3 |
2 |
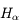
|
656 |
| 4 |
2 |
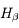
|
486 |
| 5 |
2 |
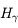
|
434 |
| 6 |
2 |
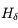
|
410 |
Les autres séries de raies (Lyman, Paschen, Brackett…) se déduisent de la même façon en modifiant le niveau d'arrivée (p = 2 pour la série de Balmer). La série de Lyman (p = 1) est située dans l'ultraviolet, les autres (p > 2) dans l'infrarouge proche.
Série de Balmer

Les quatre premières raies de la série de Balmer, en lumière visible, vues en émission (l'axe est en longueur d'onde).
Crédit :
Merikanto / Wikipedia
-
Question 2
Solution :
L'énergie émise par rayonnement correspond à une variation de l'énergie de l'atome :
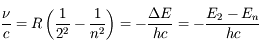
On en déduit :
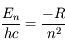
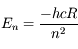
Les niveaux d'énergie varient en 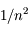
-
Question 3
Solution :
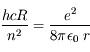
Le rayon ne peut donc prendre que des valeurs discrètes :
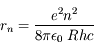
Le moment cinétique s'écrit :
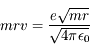
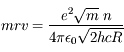
La valeur expérimentale de la constante de Rydberg est telle que :
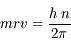
qui est l'hypothèse principale du modèle de Bohr : le moment cinétique est quantifié, ses valeurs ne peuvent être que des multiples d'un entier n appelé nombre quantique principal.
-
Question 4
Solution :
Le modèle de Bohr n'a pas d'explication physique simple dans un cadre classique. Les électrons ne peuvent être situés qu'à certaines distances du noyau, définies par n, où ils ne rayonnent pas. Ils sautent d'une position à l'autre spontannément en absorbant ou en cédant la différence d'énergie (par rayonnement ou par collision).
On voit aussi que seul le rayon intervient dans la détermination des configurations atomiques, ce qui revient à dire qu'on ne sait pas localiser l'électron plus précisément. Dans le modèle de Bohr, les électrons sont donc seulement localisés sur une couche sphérique à la distance r du noyau.
-
Question 1
Solution :
"L'année grégorienne correspond à 366 jours les années multiples de quatre et non multiples de cent sauf les année multiples de quatre cents. Sinon, l'année vaut 365 jours."
"...Sinon, l'année vaut 365 jours.", donc par défaut 365 jours, après il faut regarder quand ajouter ou soustraire un jour.
"...366 jours les années multiples de quatre...", donc 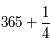 .
.
"...et non multiples de cent ...", donc 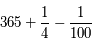 .
.
"...sauf les année multiples de quatre cents.", donc 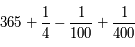 .
.
Ainsi, une année grégorienne correspond à 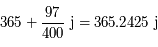
-
Question 2
Solution :
Il suffit d'évaluer l'écart avec l'année tropique. Après calcul, on obtient qu'il se produit un décalage d'un jour au bout de 3231 années.
-
Question 3
Solution :
Détermination de la fraction continue (par la méthode d'approximation d'un réel décrite précédemment), des réduites (par la relation de récurrence) et de la stabilité (au bout de combien de temps, y a-t-il décalage d'un jour?):
![\frac{p_0}{q_0} = [365]= 365](../pages_quotient/equations_quotient/equation99.png) donne un décalage d'un jour en 4 ans.
donne un décalage d'un jour en 4 ans.
![\frac{p_1}{q_1} = [365;4]= 365+\frac{1}{4}](../pages_quotient/equations_quotient/equation100.png) donne un décalage d'un jour en 128 ans.
donne un décalage d'un jour en 128 ans.
![\frac{p_2}{q_2} = [365;4;7]= 365+\frac{7}{29}](../pages_quotient/equations_quotient/equation101.png) donne un décalage d'un jour en 1232 ans.
donne un décalage d'un jour en 1232 ans.
![\frac{p_3}{q_3} = [365;4;7;1]= 365+\frac{8}{33}](../pages_quotient/equations_quotient/equation102.png) donne un décalage d'un jour en 4278 ans.
donne un décalage d'un jour en 4278 ans.
![\frac{p_4}{q_4} = [365;4;7;1;3]= 365+\frac{31}{128}](../pages_quotient/equations_quotient/equation103.png) donne un décalage d'un jour en 331455 ans.
donne un décalage d'un jour en 331455 ans.
Ainsi, la réduite 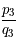 permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
Par contre 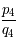 serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
-
Question 1
Solution :
Soient X et Y entiers naturels correspondant au nombre de dents sur chaque engrenage associé à une planète. Alors l'équation diophantienne à résoudre est 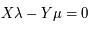 où λ est associée à la révolution de Saturne et μ de la Terre.
où λ est associée à la révolution de Saturne et μ de la Terre.
-
Question 2
Solution :
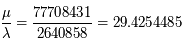 .
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
.
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
-
Question 3
Solution :
L'équation diophantienne à résoudre est 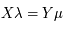 . Cela revient à trouver le rationnel
. Cela revient à trouver le rationnel 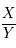 tel que
tel que 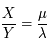 .
.
Pour supprimer le problème technique occasionné par un trop grand nombre de dents, le problème est alors résolu par approximation diophantienne, c'est-à-dire trouver un rationnel approximant convenablement  , qui est techniquement réalisable et sans une trop grande erreur. Pour cela, il faut effectuer un développement de
, qui est techniquement réalisable et sans une trop grande erreur. Pour cela, il faut effectuer un développement de  fraction continue.
fraction continue.
-
Question 4
Solution :
Il faut décomposer 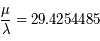 en une fraction continue tout en contrôlant la stabilité (
en une fraction continue tout en contrôlant la stabilité (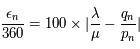 ):
):
![\frac{p_0}{q_0} = [29]= 29](../pages_quotient/equations_quotient/equation118.png) donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_1}{q_1} = [29;2]= \frac{59}{2}](../pages_quotient/equations_quotient/equation119.png) donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_2}{q_2} = [29;2;2]= \frac{147}{5}](../pages_quotient/equations_quotient/equation120.png) donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_3}{q_3} = [29;2;2;1]= \frac{206}{7}](../pages_quotient/equations_quotient/equation121.png) donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
![\frac{p_4}{q_4} = [29;2;2;1;5]= \frac{1177}{40}](../pages_quotient/equations_quotient/equation122.png) donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
Ainsi, en tenant compte qu'il est difficile de construire des engrenages comportant plus de 1000 dents et au regard de la stabilité obtenue après 100 révolutions de la Terre, le système le plus optimal serait d'utiliser une roue comportant 7 dents pour la Terre et 206 dents pour Saturne.
C'est ce qu'avait conclu Christian Huygens à son époque!
-
Question 1
Solution :
Le Soleil, la Terre et la Lune sont trois points de l'espace.
Soit 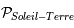 , le plan défini par l'orbite de la Terre autour du Soleil (plan de l'écliptique) et soit
, le plan défini par l'orbite de la Terre autour du Soleil (plan de l'écliptique) et soit 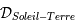 , la droite passant par la Terre et le Soleil.
, la droite passant par la Terre et le Soleil.
Il y a éclipse lorsque 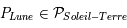 (Lune dans le plan de l'écliptique) et
(Lune dans le plan de l'écliptique) et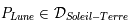 (Lune alignée sur la droite Terre-Soleil).
On notera qu'il y a éclipse de Lune si on a l'ordre
(Lune alignée sur la droite Terre-Soleil).
On notera qu'il y a éclipse de Lune si on a l'ordre 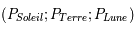 . Dans ce cas la Lune passe dans le côte d'ombre de la Terre.
Et il y a éclipse de Soleil lorsque
. Dans ce cas la Lune passe dans le côte d'ombre de la Terre.
Et il y a éclipse de Soleil lorsque 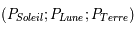 .
.
-
Question 2
Solution :
Le plan orbital de la Lune étant incliné relativement au plan de l'écliptique, une éclipse apparaît lorsque le satellite naturel de la Terre passe à l'intersection du plan orbital de la Terre et de celui de l'orbite lunaire. Sur l'ellipse décrite par la Lune, ce sont deux points appelés noeud ascendant et descendant.
En terme d'éclairement de la Lune relativement à la Terre, le fait d'appartenir à la droite 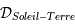 signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
-
Question 3
Solution :
En partant d'une éclipse, et donc nouvelle/pleine-lune et Lune au noeud ascendant/descendant, pour prédire une nouvelle éclipse il doit exister une équation diophantienne reliant les deux périodes. Soient X et Y entiers naturels alors l'équation diophantienne à résoudre est 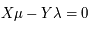 .
.
-
Question 4
Solution :
L'équation diophantienne à résoudre est 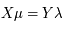 . Cela revient à trouver le rationnel
. Cela revient à trouver le rationnel 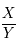 tel que
tel que 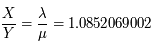 .
.
La Lune et le Soleil n'étant pas des objets ponctuels (30' d'arc de diamètre), il est possible de résoudre le problème par approximation diophantienne, c'est-à-dire trouver un rationnel approximant convenablement  tout en contrôlant l'écart de coincidence afin de vérifier qu'il y a bien éclipse (que la configuration n'est pas trop éloignée de la configuration d'éclipse total: c'est ce qu'on appelle une éclipse partielle).
tout en contrôlant l'écart de coincidence afin de vérifier qu'il y a bien éclipse (que la configuration n'est pas trop éloignée de la configuration d'éclipse total: c'est ce qu'on appelle une éclipse partielle).
-
Question 5
Solution :
Dans l'approximation des orbites circulaires, la Lune parcourt 1° en 1h48min relativement à l'axe formé par les noeuds. De même, la Lune relativement à l'axe Terre-Soleil parcourt 1° en 1h58min.
Il n'y a plus éclipse lorsque le centre de la Lune est à plus de 0.5° du passage au noeud ascendant ou à 0.5° de l'axe Terre-Soleil sur le cercle décrivant la lunaison.
Ainsi, nous pouvons considérer qu'il n'y a plus éclipse lorsque l'écart de coincidence en temps est supérieur à 54min (on regarde le minimum des deux temps de parcours pour 1° et on évalue le temps que met le centre de la Lune pour être décallé de plus de 0.5° par rapport au point donnant une éclipse totale).
Donc, pour retrouver une éclipse (totale ou partielle) à partir d'une configuration d'éclipse totale, il faut trouver deux entiers, X et Y tels que 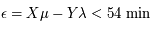 .
.
-
Question 6
Solution :
Détermination de la fraction continue (par la méthode d'approximation d'un réel décrite précédemment), des réduites (par la relation de récurrence) et des erreurs de coïncidence associées (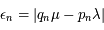 ):
):
![\frac{p_0}{q_0} = [1]= 1~~\mbox{ et } \epsilon_0 = 2\mbox{j}~7\mbox{h}38\mbox{min}](../pages_quotient/equations_quotient/equation139.png)
![\frac{p_1}{q_1} = [1;11]= \frac{12}{11}~~\mbox{ et } \epsilon_1 = 1\mbox{j}~16\mbox{h}58\mbox{min}](../pages_quotient/equations_quotient/equation140.png)
![\frac{p_2}{q_2} = [1;11;1]= \frac{13}{12}~~\mbox{ et } \epsilon_2 = 14\mbox{h}41\mbox{min}](../pages_quotient/equations_quotient/equation141.png)
![\frac{p_3}{q_3} = [1;11;1;2]= \frac{38}{35}~~\mbox{ et } \epsilon_3 = 11\mbox{h}36\mbox{min}](../pages_quotient/equations_quotient/equation142.png)
![\frac{p_4}{q_4} = [1;11;1;2;1]= \frac{51}{47}~~\mbox{ et } \epsilon_4 = 3\mbox{h}12\mbox{min}](../pages_quotient/equations_quotient/equation143.png)
![\frac{p_5}{q_5} = [1;11;1;2;1;3]= \frac{191}{176}~~\mbox{ et } \epsilon_5 = 2\mbox{h}21\mbox{min}](../pages_quotient/equations_quotient/equation144.png)
![\frac{p_6}{q_6} = [1;11;1;2;1;3;1]= \frac{242}{223}~~\mbox{ et } \epsilon_6 = 45\mbox{min}](../pages_quotient/equations_quotient/equation145.png)
-
Question 7
Solution :
Par la question précédente, nous pouvons conclure qu'après un temps correspondant à 223 lunaisons après une éclipse totale (où 242 mois draconitiques), nous sommes dans une configuration d'éclipse approchée avec un écart de 42 minutes sur la configuration exacte mais suffisamment proche de celle-ci pour que le disque lunaire intersecte le disque solaire (éclipse de Soleil) ou que le disque lunaire entre dans le cône d'ombre de la Terre (éclipse de Lune).
Ainsi, un cycle de Saros, c'est-à-dire le temps pour prédire le retour d'une éclipse (après une éclipse totale) est bien de 223 lunaisons.
-
Question 8
Solution :
Tout d'abord, 223 lunaisons correspond à 6585.38 jours, c'est-à-dire un peu plus de 18 ans. Or entre le 11 août 1999 et 2017, il y a 5 années bissextiles. Donc l'éclipse se déroulera 18 ans et 10 jours après: le 21 août 2017.
Par contre, les 0.38 jours restant impliquent que la Terre aura tourné d'un quart sur son axe ce qui correspond approximativement aux longitudes de l'Amérique du Nord. Donc, malheureusement invisible en France...
 Phénomènes mutuels
Phénomènes mutuels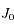 . Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
. Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
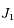 de la prochaine opposition simultanée des deux corps.
de la prochaine opposition simultanée des deux corps.
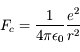
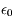 une constante physique (permittivité du vide).
une constante physique (permittivité du vide).
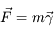 et on projette sur le rayon vecteur.
et on projette sur le rayon vecteur.
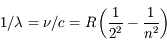
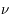 est la fréquence associée, n est un nombre entier > 2, R une constante et c la vitesse de la lumière.
est la fréquence associée, n est un nombre entier > 2, R une constante et c la vitesse de la lumière.
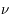 du rayonnement :
du rayonnement : 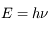 .
.
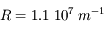 (constante de Rydberg).
(constante de Rydberg).
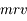 .
.

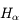 est particulièrement importante en Astronomie car elle permet de détecter l'hydrogène atomique dans le milieu interstellaire.
est particulièrement importante en Astronomie car elle permet de détecter l'hydrogène atomique dans le milieu interstellaire.
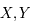 deux nombres représentant des périodes, et de trouver
deux nombres représentant des périodes, et de trouver 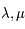 , deux entiers tels que
, deux entiers tels que 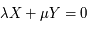 . La notion d'approximation introduite par les fractions continues est utilisée lorsque
. La notion d'approximation introduite par les fractions continues est utilisée lorsque 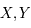 sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant
sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant 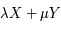 .
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
.
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
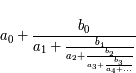 où les
où les 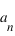 et les
et les 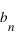 sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
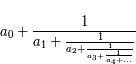 avec
avec 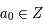 et
et 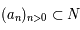 (fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire
(fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire ![[a_0;a_1;a_2;...;a_n;...]](../pages_quotient/equations_quotient/equation57.png) .
.
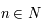 , on appellera réduite de la fraction continue définie par la suite
, on appellera réduite de la fraction continue définie par la suite 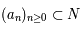 , la fraction
, la fraction ![\frac{p_n}{q_n}=[a_0;a_1;a_2;a_3;...;a_n]](../pages_quotient/equations_quotient/equation60.png) . Pour le nombre d'or
. Pour le nombre d'or 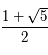 , les trois premières réduites sont
, les trois premières réduites sont ![\frac{p_0}{q_0}= [1]](../pages_quotient/equations_quotient/equation62.png) ,
, ![\frac{p_1}{q_1}=[1;1]](../pages_quotient/equations_quotient/equation63.png) ,
, ![\frac{p_2}{q_2}=[1;1;1]](../pages_quotient/equations_quotient/equation64.png) .
Ainsi, nous obtenons deux suites d'entiers
.
Ainsi, nous obtenons deux suites d'entiers 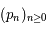 et
et 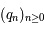 avec en particulier, la propriété suivante:
si
avec en particulier, la propriété suivante:
si 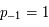 ,
, 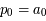 et
et 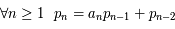 , et si
, et si 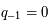 ,
, 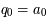 et
et 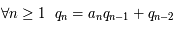 , alors
, alors ![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation73.png) .
.
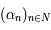 une suite de réels telle que:
une suite de réels telle que:
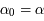 ,
,
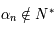 alors
alors 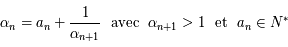 ,
,
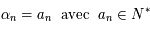 .
.
![\alpha = a_0 + \frac{1}{\alpha_1}= a_0 + \frac{1}{a_1 + \frac{1}{\alpha_2}}} = a_0 + \frac{1}{a_1 + \frac{1}{a_2+ \frac{1}{\alpha_3}}}}=...=[a_0;a_1;a_2;...;a_n+ \frac{1}{\alpha_{n+1}}]=...](../pages_quotient/equations_quotient/equation79.png)
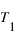 et
et 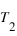 , alors afin de caractériser le retour mutuel de ces deux phénomènes, il est commode de chercher deux entiers X et Y tels que
, alors afin de caractériser le retour mutuel de ces deux phénomènes, il est commode de chercher deux entiers X et Y tels que 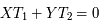 . Or généralement, les périodes ne sont malheureusement pas des nombres entiers ce qui implique de grands nombres entiers pour X et Y.
. Or généralement, les périodes ne sont malheureusement pas des nombres entiers ce qui implique de grands nombres entiers pour X et Y.
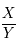 approchant
approchant 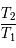 de façon à résoudre le problème au voisinage de la résonnance. C'est ce qu'on appelle l'approximation diophantienne. Nous utiliserons pour cela les fractions continues.
de façon à résoudre le problème au voisinage de la résonnance. C'est ce qu'on appelle l'approximation diophantienne. Nous utiliserons pour cela les fractions continues.
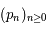 et
et 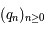 , deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
, deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
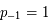 ,
, 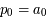 et
et 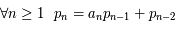 ,
,
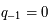 ,
, 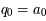 et
et 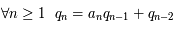 ,
,
![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation93.png) .
.
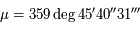 en un an. De même en un an, Saturne réalise
en un an. De même en un an, Saturne réalise 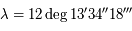 (Ce sont les valeurs de l'époque).
(Ce sont les valeurs de l'époque).
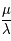 . Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
. Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
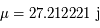 .
.
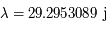 .
.
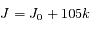 , où k est un nombre entier (relatif).
, où k est un nombre entier (relatif).
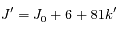 , où k' est un autre nombre entier.
, où k' est un autre nombre entier.
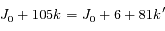 , soit
, soit 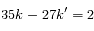 , où k et k' sont les nombres de périodes effectuées par les corps A et B entre
, où k et k' sont les nombres de périodes effectuées par les corps A et B entre 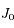 et
et 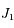 . On reconnaît une équation diophantienne, reliant trois nombres entiers.
. On reconnaît une équation diophantienne, reliant trois nombres entiers.
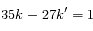 . Le couple (-10, -13) est une telle solution.
. Le couple (-10, -13) est une telle solution.
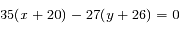 .
.
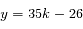
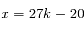 , donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
, donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
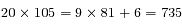 jours.
jours.
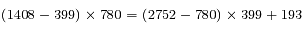 jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.
jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.
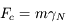 , soit :
, soit :
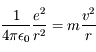
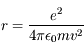
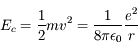
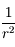 , qui dérive d'un potentiel en 1/r.
, qui dérive d'un potentiel en 1/r.
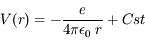
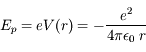
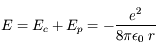
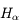
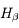
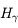
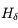

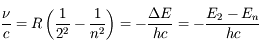
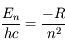
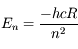
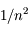
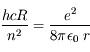
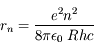
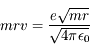
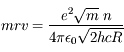
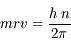
![\frac{p_{n+1}}{q_{n+1}} = [a_0;a_1;a_2;a_3;\dots;a_n;a_{n+1}]=[a_0;a_1;a_2;a_3;\dots;a_n + \frac{1}{a_{n+1}}]](../pages_quotient/equations_quotient/equation94.png) et en l'appliquant au rang n.
et en l'appliquant au rang n.
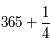 .
.
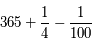 .
.
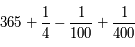 .
.
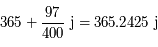
![\frac{p_0}{q_0} = [365]= 365](../pages_quotient/equations_quotient/equation99.png) donne un décalage d'un jour en 4 ans.
donne un décalage d'un jour en 4 ans.
![\frac{p_1}{q_1} = [365;4]= 365+\frac{1}{4}](../pages_quotient/equations_quotient/equation100.png) donne un décalage d'un jour en 128 ans.
donne un décalage d'un jour en 128 ans.
![\frac{p_2}{q_2} = [365;4;7]= 365+\frac{7}{29}](../pages_quotient/equations_quotient/equation101.png) donne un décalage d'un jour en 1232 ans.
donne un décalage d'un jour en 1232 ans.
![\frac{p_3}{q_3} = [365;4;7;1]= 365+\frac{8}{33}](../pages_quotient/equations_quotient/equation102.png) donne un décalage d'un jour en 4278 ans.
donne un décalage d'un jour en 4278 ans.
![\frac{p_4}{q_4} = [365;4;7;1;3]= 365+\frac{31}{128}](../pages_quotient/equations_quotient/equation103.png) donne un décalage d'un jour en 331455 ans.
donne un décalage d'un jour en 331455 ans.
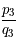 permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
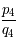 serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
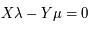 où
où 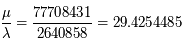 .
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
.
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
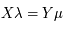 . Cela revient à trouver le rationnel
. Cela revient à trouver le rationnel 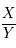 tel que
tel que 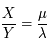 .
.
 , qui est techniquement réalisable et sans une trop grande erreur. Pour cela, il faut effectuer un développement de
, qui est techniquement réalisable et sans une trop grande erreur. Pour cela, il faut effectuer un développement de  fraction continue.
fraction continue.
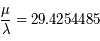 en une fraction continue tout en contrôlant la stabilité (
en une fraction continue tout en contrôlant la stabilité (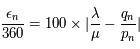 ):
):
![\frac{p_0}{q_0} = [29]= 29](../pages_quotient/equations_quotient/equation118.png) donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_1}{q_1} = [29;2]= \frac{59}{2}](../pages_quotient/equations_quotient/equation119.png) donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_2}{q_2} = [29;2;2]= \frac{147}{5}](../pages_quotient/equations_quotient/equation120.png) donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_3}{q_3} = [29;2;2;1]= \frac{206}{7}](../pages_quotient/equations_quotient/equation121.png) donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
![\frac{p_4}{q_4} = [29;2;2;1;5]= \frac{1177}{40}](../pages_quotient/equations_quotient/equation122.png) donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
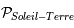 , le plan défini par l'orbite de la Terre autour du Soleil (plan de l'écliptique) et soit
, le plan défini par l'orbite de la Terre autour du Soleil (plan de l'écliptique) et soit 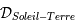 , la droite passant par la Terre et le Soleil.
, la droite passant par la Terre et le Soleil.
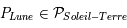 (Lune dans le plan de l'écliptique) et
(Lune dans le plan de l'écliptique) et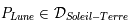 (Lune alignée sur la droite Terre-Soleil).
On notera qu'il y a éclipse de Lune si on a l'ordre
(Lune alignée sur la droite Terre-Soleil).
On notera qu'il y a éclipse de Lune si on a l'ordre 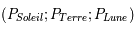 . Dans ce cas la Lune passe dans le côte d'ombre de la Terre.
Et il y a éclipse de Soleil lorsque
. Dans ce cas la Lune passe dans le côte d'ombre de la Terre.
Et il y a éclipse de Soleil lorsque 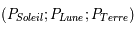 .
.
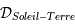 signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
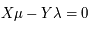 .
.
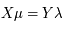 . Cela revient à trouver le rationnel
. Cela revient à trouver le rationnel 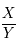 tel que
tel que 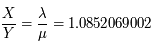 .
.
 tout en contrôlant l'écart de coincidence afin de vérifier qu'il y a bien éclipse (que la configuration n'est pas trop éloignée de la configuration d'éclipse total: c'est ce qu'on appelle une éclipse partielle).
tout en contrôlant l'écart de coincidence afin de vérifier qu'il y a bien éclipse (que la configuration n'est pas trop éloignée de la configuration d'éclipse total: c'est ce qu'on appelle une éclipse partielle).
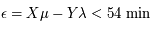 .
.
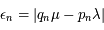 ):
):
![\frac{p_0}{q_0} = [1]= 1~~\mbox{ et } \epsilon_0 = 2\mbox{j}~7\mbox{h}38\mbox{min}](../pages_quotient/equations_quotient/equation139.png)
![\frac{p_1}{q_1} = [1;11]= \frac{12}{11}~~\mbox{ et } \epsilon_1 = 1\mbox{j}~16\mbox{h}58\mbox{min}](../pages_quotient/equations_quotient/equation140.png)
![\frac{p_2}{q_2} = [1;11;1]= \frac{13}{12}~~\mbox{ et } \epsilon_2 = 14\mbox{h}41\mbox{min}](../pages_quotient/equations_quotient/equation141.png)
![\frac{p_3}{q_3} = [1;11;1;2]= \frac{38}{35}~~\mbox{ et } \epsilon_3 = 11\mbox{h}36\mbox{min}](../pages_quotient/equations_quotient/equation142.png)
![\frac{p_4}{q_4} = [1;11;1;2;1]= \frac{51}{47}~~\mbox{ et } \epsilon_4 = 3\mbox{h}12\mbox{min}](../pages_quotient/equations_quotient/equation143.png)
![\frac{p_5}{q_5} = [1;11;1;2;1;3]= \frac{191}{176}~~\mbox{ et } \epsilon_5 = 2\mbox{h}21\mbox{min}](../pages_quotient/equations_quotient/equation144.png)
![\frac{p_6}{q_6} = [1;11;1;2;1;3;1]= \frac{242}{223}~~\mbox{ et } \epsilon_6 = 45\mbox{min}](../pages_quotient/equations_quotient/equation145.png)