Intégrale de Riemann
- Introduction
- Longueur d'une courbe, aire d'une surface
- Redshift
- Ex: Redshift
- Calotte sphérique
- Ex : Calotte sphérique
- Potentiel gravitationnel de la Terre
- Ex: Potentiel gravitationnel de la Terre
- Théorèmes
- Supernova 1A
- Ex: Supernova 1A
- Bruit de numérisation
- Ex: bruit de numérisation
- Intégrales Généralisées
- Loi de Stefan
- Ex : loi de Stefan
- Distribution des vitesses de Maxwell
- Ex: Distribution des vitesses de Maxwell
- Temps de vie d'une étoile
- Ex: Temps de vie d'une étoile
Introduction
On trouvera dans cette partie les exercices suivants :
- Détermination de la relation entre redshift et facteur d'échelle (changement de variable d'intégration)
- Calcul de la surface d'une calotte sphérique (aire d'une surface)
- Calcul du potentiel terrestre en modélisant l'aplatissement équatorial par un anneau (intégrales définies)
- Détermination du redshift d'une supernova (changement de variable d'intégration)
- Calcul du bruit de numérisation dans une caméra CCD (intégrales définies)
- Démonstration de la loi de Stefan pour les corps noirs (intégrales généralisées)
- Calcul de la distribution des vitesses moléculaires dans un gaz (intégrales généralisées)
- Calcul du temps de vie d'une étoile (intégrales généralisées)
Longueur d'une courbe, aire d'une surface
Auteurs: Jérôme Thiébaut, Marc Fouchard, Alain Vienne
Redshift
Auteur : Jérôme Thiébaut
En coordonnées cartésiennes, un élément de longueur 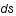 se calcule selon le théorème de Pythagore:
se calcule selon le théorème de Pythagore:
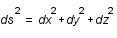 .
.
Ceci donne en coordonnées sphériques:
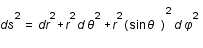 .
.
On voit que l'expression de 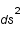 dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
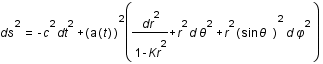 ,
,
ou 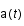 est le facteur d'échelle qui décrit l'expansion de l'univers,
est le facteur d'échelle qui décrit l'expansion de l'univers, 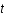 le temps,
le temps, 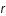 ,
, 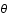 et
et 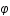 les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) ,
les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) , 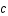 la vitesse de la lumière et
la vitesse de la lumière et 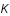 la courbure de l'univers.
la courbure de l'univers.
Pour un photon, la trajectoire est telle que 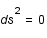 .
.
On se propose dans cet exercice d'étudier la trajectoire d'un photon radial afin de relier le redshift (ou décallage spectral), 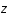 , au facteur d'échelle,
, au facteur d'échelle, 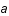 .
.
Ex: Redshift
Auteur: Jérôme Thiébaut
 Redshift
Redshift
Difficulté : ☆☆
Temps : 20mn
On considère un photon radial émis à une distance 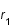 au temps
au temps 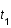 par une galaxie lointaine. Ce photon nous est reçu au temps
par une galaxie lointaine. Ce photon nous est reçu au temps 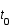 en
en 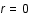 .
.
Sa trajectoire est décrite par la métrique: 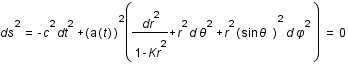 .
.
Question 1)
Simplifier la métrique compte tenu de la nature du photon et exprimer l'égalité sous forme intégrale.
Le photon étant radial, 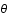 et
et 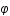 sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
Question 2)
Un deuxième photon est émis à 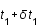 et est reçu en
et est reçu en 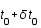 . Quelle est la nouvelle égalité sous forme intégrale ?
. Quelle est la nouvelle égalité sous forme intégrale ?
Question 3)
Sachant que 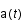 est considéré comme constant pendant un temps
est considéré comme constant pendant un temps 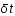 faible et que la distance comobile (
faible et que la distance comobile (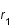 ) est constante par définition, montrer que
) est constante par définition, montrer que 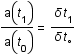 .
.
Décomposer l'intégrale par la relation de Chasles.
Calotte sphérique
Ex : Calotte sphérique
Auteur: Marc Fouchard
 Calotte sphérique
Calotte sphérique
Difficulté : ☆
Temps : 30 mn
Question 1)
Faire la figure qui correspond à l'énoncé.
Potentiel gravitationnel de la Terre
Auteur : Alain Vienne
Le potentiel gravitaionnel de la Terre est souvent modélisé par:
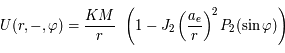
avec 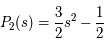
C'est le potentiel évalué en un point 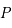 de coordonnées sphériques
de coordonnées sphériques 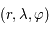 (dont le plan horizontal est la plan de l'équateur).
(dont le plan horizontal est la plan de l'équateur).
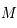 est la masse totale de la Terre et
est la masse totale de la Terre et 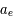 son rayon équatorial (
son rayon équatorial (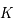 la constante de gravitation universelle).
la constante de gravitation universelle). 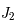 est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de
est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de 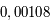 .
.
Dans l'exercice qui suit, nous allons évaluer le potentiel d'un anneau massif et homogène. Nous verrons que l'expression obtenue aura exactement la même forme que celle ci-dessus.
Un exemple d'application concerne la prise en compte de la gravitation des anneaux de Saturne: il suffit de réévaluer le cooefficient d'aplatissement 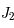 de Saturne.
de Saturne.
Voici un autre exercice sur le potentiel gravitationnel terrestre.
Ex: Potentiel gravitationnel de la Terre
Auteur: Alain Vienne
 Potentiel gravitationnel de la Terre
Potentiel gravitationnel de la Terre
Difficulté : ☆
Temps : 1h
Question 2)
Calculer 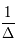 en se limitant aux termes de degré 2 au plus en
en se limitant aux termes de degré 2 au plus en 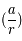 .
.
Question 4)
En comparant cette expression avec celle utilisant le coefficient 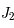 , donner le rayon de l'anneau correspondant au potentiel terrestre. On donne
, donner le rayon de l'anneau correspondant au potentiel terrestre. On donne 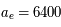 km.
km.
Théorèmes
Auteur: Jérôme Thiébaut, Stéphane Erard
Supernova 1A
Auteur: Jérôme Thiébaut
Les supernovae de type 1A correspondent à l'explosion d'une étoile de type naine blanche suite à l'accrétion de matière arrachée à une étoile géante proche. Ces phénomènes extrêmement lumineux sont visibles de très loin ce qui permet leurs détections. La courbe de luminosité d'une SN1A est caractéristique et permet de déterminer sa magnitude absolue. Le but de cet exercice est de montrer comment grâce à des mesures de luminosité, on peut déterminer le redshift de l'étoile, et donc de la galaxie hôte. Le redshift étant une mesure de la distance, les SN1A servent de balises pour mesurer les distances dans l'univers.
Courbe de lumière d'une supernova.
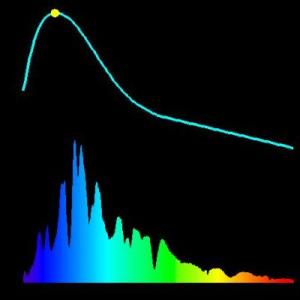
Courbe de lumière et spectre au maximum d'intensité d'une supernova.
Crédit :
Supernova Cosmology Project, Berkeley University
Ex: Supernova 1A
Auteur: Jérôme Thiébaut
 Supernova 1A
Supernova 1A
Difficulté : ☆
Temps : 30 min
On observe une supernova de type 1A dans une galaxie et on mesure sa magnitude apparente 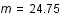 . Grâce à sa courbe de lumière, on détermine sa magnitude absolue
. Grâce à sa courbe de lumière, on détermine sa magnitude absolue 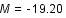 .
.
Question 1)
On exprime la distance luminosité, 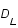 , comme suit:
, comme suit:
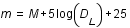 , où
, où 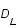 est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à
est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à 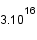 m).
m).
Calculer sa valeur.
Question 3)
Calculer r, puis sachant que la distance luminosité et la distance r sont reliées par la relation 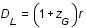 (dans le modèle cosmologique standart
(dans le modèle cosmologique standart 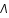 CDM), déterminer l'équation du second degré à laquelle obéit
CDM), déterminer l'équation du second degré à laquelle obéit 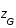 .
.
Question 4)
Résoudre cette équation et déterminer la valeur du redshift 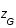 (positive par définition).
On donne
(positive par définition).
On donne  et
et 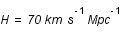 .
.
Bruit de numérisation
Auteur: Stéphane Erard
Les instruments modernes utilisent des détecteurs numériques tels que des CCD, c'est-à-dire qu'ils fournissent en sortie un signal numérisé sur un nombre fini de valeurs. Cette étape produit une erreur d'arrondi appelée "bruit de quantification" ou "bruit de numérisation" qui peut dans certains cas limiter la précision de la mesure. On étudie ici la statistique de ce bruit.
Ex: bruit de numérisation
Auteur: Stéphane Erard
 Bruit de numérisation
Bruit de numérisation
Difficulté : ☆
Temps : 30 min
L'exercice consiste à estimer l'erreur due à la numérisation (ou quantification) d'un signal continu.
Question 1)
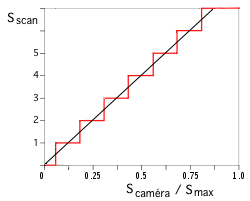
On mesure un signal lumineux avec une caméra CCD. Tracer l'allure de la fonction de réponse du convertisseur analogique/numérique (CAN). Si le convertisseur fonctionne sur 12 bits, combien de valeurs sont disponibles en sortie ?
Le convertisseur est réglé pour couvrir la dynamique de la caméra jusqu'à un niveau analogique 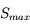 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?
Question 2)
Estimer l'erreur quadratique moyenne due à la numérisation.
L'erreur est la différence entre le signal d'entrée et le signal de sortie, similaire à une erreur d'arrondi :
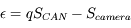
On commence par corriger de l'erreur systématique (biais, ou offset) en centrant la différence — ce biais est de 1/2 pas-codeur :
Offset
Question 3)
Calculer le rapport signal sur bruit correspondant. Comment peut-on améliorer celui-ci, et jusqu'à quel point ?
Question 4)
Comparer aux autres sources de bruit.
Intégrales Généralisées
Auteurs: Marc Fouchard, Stéphane Erard, S. Renner
Loi de Stefan
Ex : loi de Stefan
Auteur: Marc Fouchard
 loi de Stefan
loi de Stefan
Difficulté : ☆☆
Temps : 1h
Question 2)
L'énergie totale 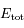 est donnée par :
est donnée par :
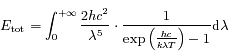 .
.
Montrer, en effectuant un changement de variable approprié, que 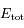 peut s'écrire sous la forme:
peut s'écrire sous la forme:
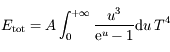
où 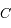 est une constante que l'on déterminera.
est une constante que l'on déterminera.
On pourra faire le changement de variable 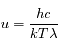 .
.
Question 3)
Montrer que l'intégrale
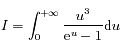
est convergente.
 Remarque
Remarque
Cette intégrale est une fonction zeta de Reimann. On peut montrer que 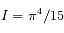 .
.
Question 4)
En déduire la loi de Stefan:
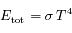
où 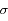 est une constante que l'on déterminera.
est une constante que l'on déterminera.
Distribution des vitesses de Maxwell
Auteur: Stéphane Erard
On considère un gaz en équilibre, pour lequel on veut connaître les vitesses des molécules. La théorie cinétique des gaz ne donne qu'une valeur moyenne (la vitesse quadratique moyenne) :
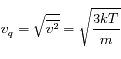
où m est la masse des molécules, T est la température, k la constante de Boltzman.
On cherche ici la distribution de vitesse, c'est-à-dire la probabilité d'avoir une vitessse comprise entre v et v+dv. Le calcul qui suit est classique (non quantique) et reproduit l'étude de Maxwell au XIXe siècle.
Ex: Distribution des vitesses de Maxwell
Auteur: Stéphane Erard
 Intégrales gaussiennes
Intégrales gaussiennes
Difficulté : ☆☆
Temps : 60 min
Le calcul des propriétés de la loi normale suppose l'intégration de la fonction gaussienne, et des intégrales similaires apparaissent dans le calcul suivant.
Le moment d'ordre n de la loi normale réduite (de moyenne nulle) est :
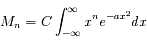
où a > 0 et n ≥ 0, C étant une constante de normalisation. On s'intéresse ici à :
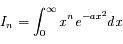
Question 1)
Trouver une relation de récurrence entre les intégrales 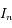 .
.
On intègre par partie en posant
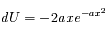
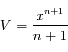
Question 2)
Calculer 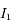 . Que représente cette quantité ?
. Que représente cette quantité ?
Question 3)
Calculer l'intégrale de Gauss 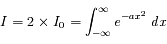
Question 4)
En déduire les moments de la loi normale centrée.
Auteur: Stéphane Erard
 Distribution des vitesses
Distribution des vitesses
Difficulté : ☆☆
Temps : 60 min
La probabilité pour qu'une molécule ait une vitesse comprise entre 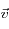 et
et 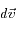 est notée
est notée 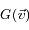 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une atmosphère planétaire , ou dans un nuage de gaz interstellaire), G ne dépend que du module de la vitesse.
Question 1)
Ecrire les conditions d'indépendance entre les composantes du vecteur vitesse, et d'isotropie.
Question 2)
En déduire la forme de G.
Question 3)
Identifier deux conditions qui permettent de calculer les coefficients ci-dessus.
Question 4)
Calculer les intégrales 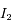 et
et 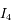 de l'exercice précédent.
de l'exercice précédent.
Question 5)
En dériver l'expression de 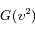 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
Question 6)
En dériver l'expression de 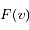 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.
Question 7)
Tracer cette fonction, expliquer sa forme.
Question 8)
Comment peut-on utiliser cette fonction pour expliquer l'évolution des atmosphères planétaires ?
Temps de vie d'une étoile
Auteur : S. Renner
On estime ici la durée de vie d'une étoile de type solaire, en supposant tout d'abord que la seule source d'énergie est la gravitation, puis en considérant le cas réel des réactions de fusion thermonucléaire de l'hydrogène en hélium. La première hypothèse (dissipation de l'énergie gravitationnelle) est une idée qui apparaît avec les travaux de Kelvin au XIXe siècle.
Ex: Temps de vie d'une étoile
Auteur: S. Renner
 Temps de vie d'une étoile
Temps de vie d'une étoile
Difficulté : ☆
Temps : 1h
On assimile l'étoile à une sphère homogène de masse 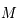 et de rayon
et de rayon 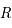 .
.
Question 1)
Montrer que son énergie de liaison gravitationnelle est 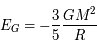 .
.
On considérera le travail élémentaire 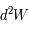 d'une couronne sphérique d'épaisseur
d'une couronne sphérique d'épaisseur 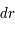 .
.
L'énergie de liaison gravitationnelle sera alors donnée par 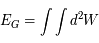 , en prenant les bornes d'intégration adéquates.
, en prenant les bornes d'intégration adéquates.
Question 3)
Même question en considérant le cas réel des réactions de fusion nucléaire de l'hydrogène en hélium au coeur du Soleil. On suppose que 10% de la masse 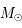 est convertie en hélium et que la luminosité
est convertie en hélium et que la luminosité 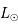 reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie
reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie 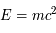 .
.
Question 4)
Le Soleil brille depuis 4.5 milliards d'années. Combien a t-il perdu en masse ?
Réponses aux exercices
pages_mesure/za2.html
Exercice
'Redshift'
-
Question 1
Aide :
Le photon étant radial, 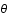 et
et 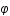 sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
Solution :
Le photon étant radial, 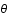 et
et 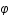 sont choisis comme nuls. On peut donc simplifier la métrique:
sont choisis comme nuls. On peut donc simplifier la métrique:
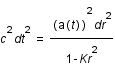 soit
soit 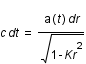 .
.
Et sous forme intégrale: 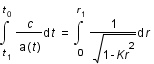
-
Question 2
Solution :
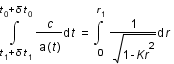
-
Question 3
Aide :
Décomposer l'intégrale par la relation de Chasles.
Solution :
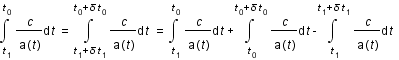
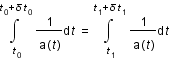
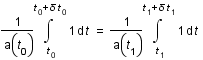
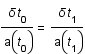
-
Question 4
Solution :
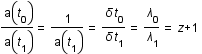
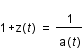
pages_mesure/exo-calotte.html
Exercice
'Calotte sphérique'
pages_mesure/exo-potentiel-terre.html
Exercice
'Potentiel gravitationnel de la Terre'
pages_theoremes/ex-sn1a.html
Exercice
'Supernova 1A'
-
Question 1
Solution :
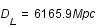
-
Question 2
Aide :
En partant de 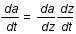 exprimer
exprimer 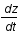 en fonction de z et H.
en fonction de z et H.
Solution :
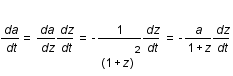
d'où 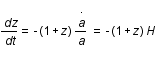
finalement 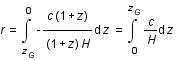
-
Question 3
Solution :
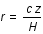 donc
donc 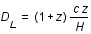 .
.
L'équation cherchée est finalement 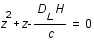 .
.
-
Question 4
Solution :
z=0.8 ce qui correspond à une distance radiale d'environ 2.15 Gpc.
pages_theoremes/exbnum.html
Exercice
'Bruit de numérisation'
-
Question 1
Solution :
Le signal d'entrée, continu, est mesuré par le CCD puis numérisé par le CAN. La sortie est donc discrète, codée sur 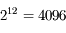 niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou pas-codeurs en français.
La courbe de réponse donne la sortie du système de mesure en fonction de son entrée :
Numérisation
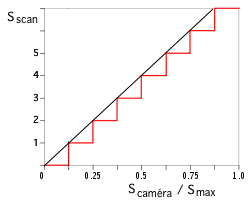
Sur n bits, le pas de numérisation du signal de sortie est q = 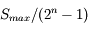
-
Question 2
Aide :
L'erreur est la différence entre le signal d'entrée et le signal de sortie, similaire à une erreur d'arrondi :
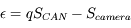
On commence par corriger de l'erreur systématique (biais, ou offset) en centrant la différence — ce biais est de 1/2 pas-codeur :
Offset

Solution :
L'erreur quadratique moyenne se calcule de façon classique :
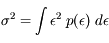
Après correction du biais, la densité de probabilité de l'erreur est uniforme dans l'intervalle [-q/2, q/2] :
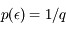 dans l'intervalle [-q/2, q/2]
dans l'intervalle [-q/2, q/2]
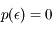 ailleurs
ailleurs
Erreur de numérisation
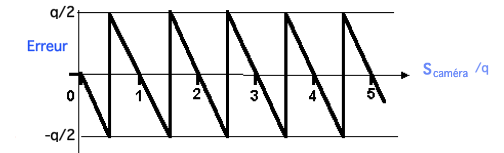
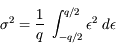
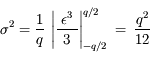
Soit un écart-type 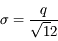 ou encore
ou encore 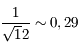 bits.
bits.
(on remarque que le coefficient 1/12 provient de l'intégration, et n'a rien à voir avec le nombre de bits utilisés)
-
Question 3
Solution :
Le signal maximum est 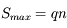 . En rapportant au signal moyen, on trouve :
. En rapportant au signal moyen, on trouve :
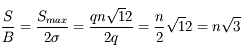
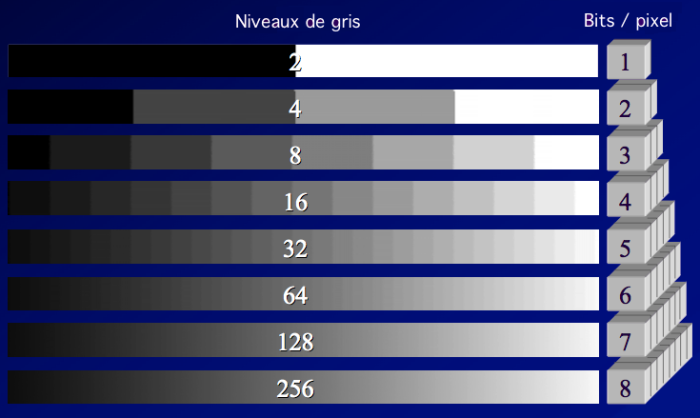
La seule façon de réduire le bruit de numérisation est de coder le signal sur un plus grand nombre de bits n. La différence de "grain" est très perceptible à l'œil nu avec une échelle de gris codée sur un nombre variable de bits. A partir de 256 niveaux, la variation apparaît quasiment continue, ce qui veut dire que le pas de quantification devient petit devant l'incertitude de lecture de l'œil. De la même façon, les CD audio sont codés sur 16 bits pour éliminer le bruit de numérisation ; celui-ci est encore très audible avec un codage sur 8 bits.
Résolution numérique
-
Question 4
Solution :
On ajuste habituellement le pas de numérisation pour coder le bruit physique sur 1 pas-codeur : un pas plus petit n'apporterait pas d'information supplémentaire sur le signal. En général, c'est le bruit de lecture qui domine le bruit intrinsèque de la source (bruit de photon). Le bruit de numérisation est alors bien plus petit. Si la chaîne de détection est bien réglée, celui-ci ne limite donc jamais la mesure.
pages_int-gen/exo-loi-de-stefan-int-gen.html
Exercice
'loi de Stefan'
pages_int-gen/exo-maxwell.html
Exercice
'Intégrales gaussiennes'
-
Question 1
Aide :
On intègre par partie en posant
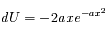
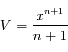
Solution :
On trouve
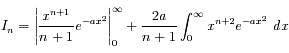
Soit
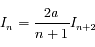
-
Question 2
Solution :
En posant 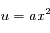 on trouve :
on trouve :
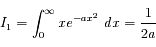
Cette quantité n'est pas proportionnelle à la moyenne de la loi normale centrée, qui est l'intégrale étendue à toute la droite réelle. Celle-ci est nulle, comme tous les moments d'ordre impair, ce qui dérive de la parité de la fonction.
-
Question 3
Solution :
La méthode la plus simple est de calculer le carré de l'intégrale et de passer en coordonnées polaires. On trouve au final :
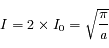
D'où le coefficient habituel de la loi normale qui normalise l'intégrale à 1.
-
Question 4
Solution :
La fonction étant paire, tous les moments d'ordre impair sont nuls. Les moments pairs suivent la relation de récurrence donnée plus haut à partir de 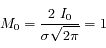 (normalisation de la densité de probabilité).
(normalisation de la densité de probabilité).
pages_int-gen/exo-maxwell.html
Exercice
'Distribution des vitesses'
-
Question 1
Solution :
En posant 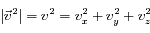
l'indépendance entre composantes de vitesse s'écrit :
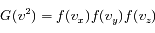
L'isotropie se traduit par :
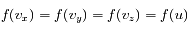 Soit :
Soit : 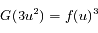
On peut donc écrire :
![G(v_x^2+v_y^2+v_z^2) = \left[G(3v_x^2) G(3v_y^2) G(3v_z^2)\right]^{1/3}](../pages_int-gen/equations_int-gen/equation66.png)
-
Question 2
Solution :
On prend le logarithme et on pose 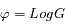 :
:
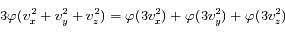
C'est la définition d'une fonction linéaire. On a donc :
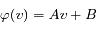
Soit
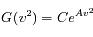
-
Question 3
Solution :
G est une densité de probabilité, elle est donc normalisée :
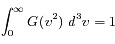
Par ailleurs on connaît la vitesse quadratique moyenne :
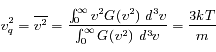
-
Question 4
Solution :
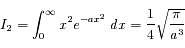
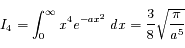
-
Question 5
Solution :
La condition de normalisation est :
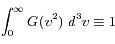
où 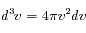 en coordonnées sphériques. Ceci donne :
en coordonnées sphériques. Ceci donne :
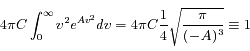
La vitesse quadratique moyenne donne :
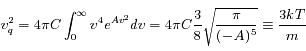
Le rapport des deux conditions conduit à :
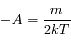 d'où
d'où 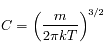
On en conclut :
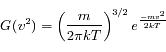
-
Question 6
Solution :
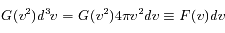
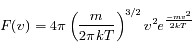
qu'on appelle distribution de Maxwell-Boltzman.
-
Question 7
Solution :
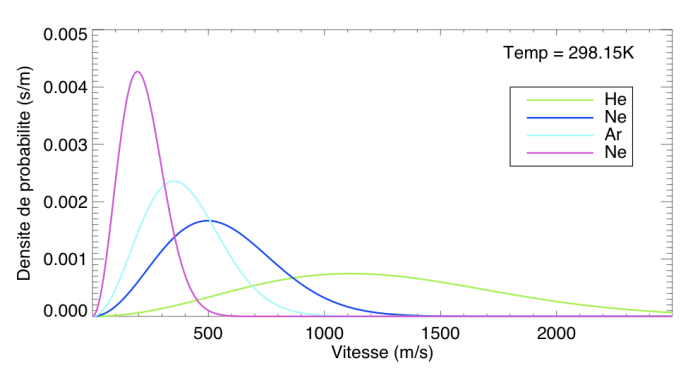
Distributions de Maxwell pour différents gaz rares à température ambiante.
Le maximum de la fonction n'est pas dû à la gaussienne elle-même (il est loin de la moyenne de celle-ci qui est centrée), mais au produit de la queue de la gaussienne par un polynôme de degré 2.
-
Question 8
Solution :
En utilisant la température qui règne au sommet de l'atmosphère, la fonction permet de calculer la distribution de vitesse des différentes espèces moléculaires ou atomiques. On peut comparer celle-ci à la vitesse d'échappement de la planète, qui dépend de sa gravité et de son rayon (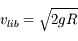 ).
).
Si une fraction significative des molécules a une vitesse supérieure à la vitesse de libération, cette espèce s'échappera rapidement de la haute atmosphère — c'est la raison première pour laquelle la Lune n'a pas d'atmosphère, alors que la Terre conserve la sienne à la même distance du Soleil.
En dehors de ce mécanisme d'échappement thermique, il existe d'autres mécanismes d'échappement atmosphérique.
pages_int-gen/exo-tps-vie-etoile-int-gen.html
Exercice
'Temps de vie d'une étoile'
-
Question 1
Aide :
On considérera le travail élémentaire 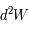 d'une couronne sphérique d'épaisseur
d'une couronne sphérique d'épaisseur 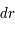 .
.
L'énergie de liaison gravitationnelle sera alors donnée par 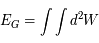 , en prenant les bornes d'intégration adéquates.
, en prenant les bornes d'intégration adéquates.
Solution :
Travail élémentaire : 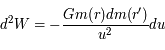
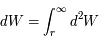
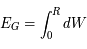
-
Question 2
Solution :
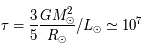 ans.
ans.
-
Question 3
Solution :
durée de vie = 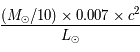 = 10 milliards d'années.
= 10 milliards d'années.
-
Question 4
Solution :
masse du Soleil transformée en énergie à chaque seconde = 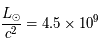 kg/s.
kg/s.
masse perdue par le Soleil = 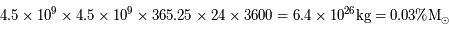 .
.
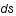 se calcule selon le théorème de Pythagore:
se calcule selon le théorème de Pythagore:
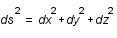 .
.
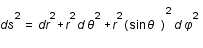 .
.
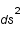 dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
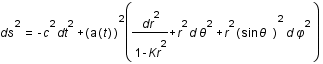 ,
,
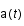 est le facteur d'échelle qui décrit l'expansion de l'univers,
est le facteur d'échelle qui décrit l'expansion de l'univers, 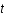 le temps,
le temps, 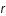 ,
, 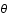 et
et 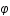 les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) ,
les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) , 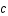 la vitesse de la lumière et
la vitesse de la lumière et 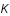 la courbure de l'univers.
la courbure de l'univers.
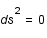 .
.
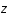 , au facteur d'échelle,
, au facteur d'échelle, 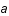 .
.
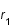 au temps
au temps 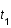 par une galaxie lointaine. Ce photon nous est reçu au temps
par une galaxie lointaine. Ce photon nous est reçu au temps 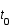 en
en 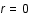 .
.
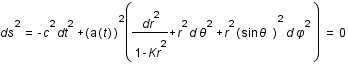 .
.
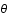 et
et 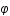 sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
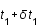 et est reçu en
et est reçu en 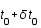 . Quelle est la nouvelle égalité sous forme intégrale ?
. Quelle est la nouvelle égalité sous forme intégrale ?
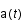 est considéré comme constant pendant un temps
est considéré comme constant pendant un temps 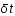 faible et que la distance comobile (
faible et que la distance comobile (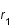 ) est constante par définition, montrer que
) est constante par définition, montrer que 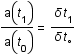 .
.
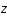 est défini comme suit:
est défini comme suit:
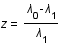 , où
, où 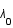 est la longueur d'onde du photon reçu et
est la longueur d'onde du photon reçu et 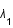 celle du photon émis.
celle du photon émis.
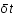 correspond une longueur d'onde
correspond une longueur d'onde 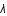 , et que par convention,
, et que par convention, 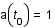 , relier la quantité
, relier la quantité 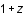 au facteur d'échelle.
au facteur d'échelle.
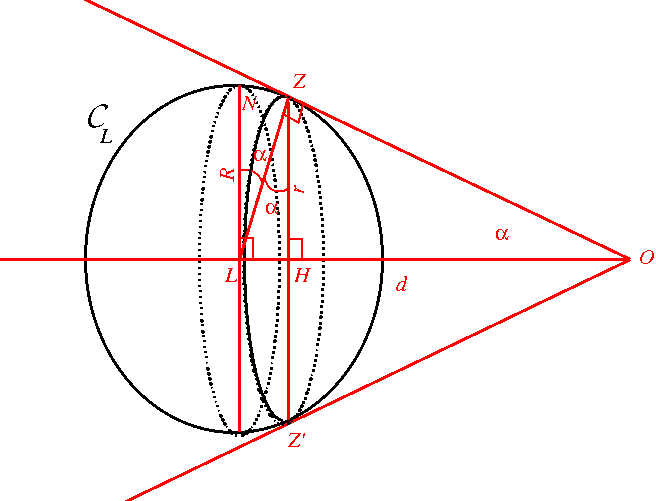
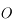 l'observateur,
l'observateur, 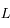 le centre de la Lune et
le centre de la Lune et 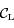 l'intersection de la sphère correspondant à la Lune avec un plan contenant la droite
l'intersection de la sphère correspondant à la Lune avec un plan contenant la droite 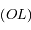 . Ainsi
. Ainsi 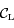 est un cercle de centre
est un cercle de centre 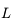 et de rayon
et de rayon 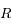 , où
, où 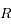 est le rayon de la Lune. On note
est le rayon de la Lune. On note 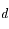 la distance
la distance 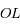 . Les tangentes à
. Les tangentes à 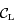 passant par
passant par 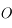 coupent
coupent 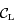 en
en 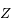 et
et 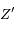 . Soit
. Soit 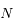 le point de
le point de 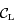 tel que
tel que 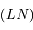 est perpendiculaire à
est perpendiculaire à 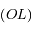 avec
avec 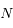 du même coté que
du même coté que 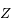 de la droite
de la droite 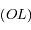 . On note
. On note 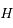 le projeté orthogonal de
le projeté orthogonal de 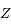 sur
sur 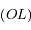 ,
, 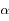 l'angle
l'angle 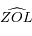 et
et 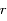 la distance
la distance 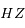 .
.
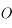 correspond donc à la partie de la surface de la Lune tournée vers
correspond donc à la partie de la surface de la Lune tournée vers 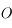 et de frontière le cercle de centre
et de frontière le cercle de centre 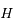 et de rayon
et de rayon 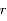 .
.
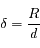 , calculer
, calculer 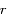 en fonction de
en fonction de 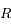 et
et 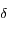 .
.
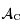 de la calotte visible depuis
de la calotte visible depuis 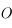 en fonction de la surface d'un hémisphère de la Lune
en fonction de la surface d'un hémisphère de la Lune 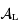 et de
et de 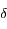 .
.
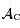 de la Terre visible par l'astronaute s'écrit sous la forme de la surface d'un cercle dont on déterminera le rayon en fonction du rayon de la Terre
de la Terre visible par l'astronaute s'écrit sous la forme de la surface d'un cercle dont on déterminera le rayon en fonction du rayon de la Terre 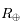 et de l'altitude
et de l'altitude 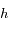 de l'astronaute. On supposera donc que
de l'astronaute. On supposera donc que 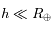 .
.
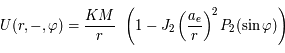
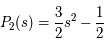
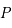 de coordonnées sphériques
de coordonnées sphériques 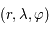 (dont le plan horizontal est la plan de l'équateur).
(dont le plan horizontal est la plan de l'équateur).
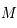 est la masse totale de la Terre et
est la masse totale de la Terre et 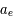 son rayon équatorial (
son rayon équatorial (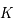 la constante de gravitation universelle).
la constante de gravitation universelle). 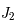 est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de
est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de 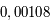 .
.
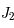 de Saturne.
de Saturne.
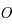 et de rayon
et de rayon 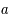 . On repère un point
. On repère un point 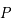 de coordonnées sphériques
de coordonnées sphériques 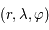 (dont le plan horizontal est le plan de l'anneau).
(dont le plan horizontal est le plan de l'anneau).
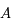 un point de l'anneau. Il fait un angle
un point de l'anneau. Il fait un angle 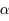 avec le premier axe (même origine que l'angle
avec le premier axe (même origine que l'angle 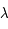 ).
).
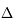 de
de 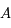 à
à 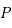 .
.
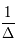 en se limitant aux termes de degré 2 au plus en
en se limitant aux termes de degré 2 au plus en 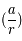 .
.
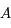 variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à
variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à 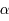 qui varie de
qui varie de 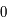 à
à 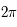 .
.
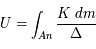 .
.
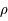 la masse linéique, on peut écrire
la masse linéique, on peut écrire 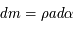 . L'anneau est homogène donc
. L'anneau est homogène donc 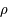 est constant.
est constant.
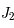 , donner le rayon de l'anneau correspondant au potentiel terrestre. On donne
, donner le rayon de l'anneau correspondant au potentiel terrestre. On donne 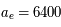 km.
km.

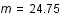 . Grâce à sa courbe de lumière, on détermine sa magnitude absolue
. Grâce à sa courbe de lumière, on détermine sa magnitude absolue 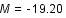 .
.
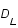 , comme suit:
, comme suit:
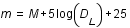 , où
, où 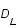 est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à
est exprimée en mégaparsec (Mpc) (Le parsec étant une unité de distance correspondant à 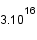 m).
m).
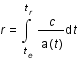 , où c est la vitesse de la lumière, t le temps,
, où c est la vitesse de la lumière, t le temps, 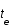 le temps d'émission de la lumière par la galaxie,
le temps d'émission de la lumière par la galaxie, 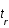 celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
celui de réception par l'observateur et a(t) le facteur d'échelle décrivant l'expansion de l'univers.
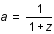 et que par définition
et que par définition 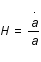 ; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à
; exprimer la distance r sous forme d'une intégrale selon z (on posera qu'à 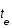 ,
, 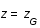 et par définition à
et par définition à 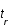 , z=0).
, z=0).
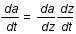 exprimer
exprimer 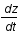 en fonction de z et H.
en fonction de z et H.
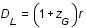 (dans le modèle cosmologique standart
(dans le modèle cosmologique standart 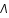 CDM), déterminer l'équation du second degré à laquelle obéit
CDM), déterminer l'équation du second degré à laquelle obéit 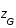 .
.
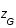 (positive par définition).
On donne
(positive par définition).
On donne  et
et 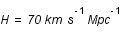 .
.
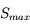 . Quel est le pas de numérisation du signal ?
. Quel est le pas de numérisation du signal ?
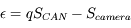

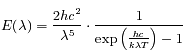
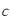 correspond à la vitesse de la lumière dans le vide,
correspond à la vitesse de la lumière dans le vide, 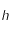 est la constante de Planck,
est la constante de Planck, 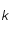 la constante de Boltzmann,
la constante de Boltzmann, 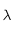 la longueur d'onde à laquelle le rayonnement est émis et
la longueur d'onde à laquelle le rayonnement est émis et 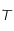 la température de surface du corps noir.
la température de surface du corps noir.
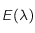 pour différente température de surface du corps noir. Sachant que l'énergie totale
pour différente température de surface du corps noir. Sachant que l'énergie totale 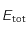 émise par le corps noir par seconde et par unité de surface correspond à l'aire comprise en l'axe des abcisses et la courbe, on remarque que
émise par le corps noir par seconde et par unité de surface correspond à l'aire comprise en l'axe des abcisses et la courbe, on remarque que 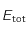 augmente avec la température de surface du corps noir (il ne faut pas cocher la case "normaliser").
augmente avec la température de surface du corps noir (il ne faut pas cocher la case "normaliser").
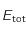 et la température de surface
et la température de surface 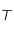 du corps noir.
du corps noir.

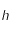 ,
, 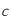 et
et 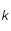 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 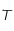 étant mesurée en degré Kelvin est aussi strictement positive, montrer que
étant mesurée en degré Kelvin est aussi strictement positive, montrer que 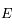 est de classe
est de classe 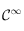 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation18.png) et est toujours strictement positive sur cet intervalle.
et est toujours strictement positive sur cet intervalle.
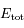 est donnée par :
est donnée par :
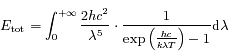 .
.
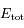 peut s'écrire sous la forme:
peut s'écrire sous la forme:
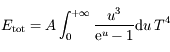
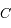 est une constante que l'on déterminera.
est une constante que l'on déterminera.
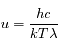 .
.
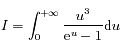
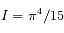 .
.
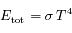
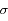 est une constante que l'on déterminera.
est une constante que l'on déterminera.
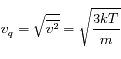
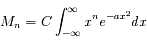
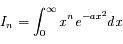
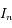 .
.
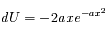
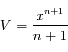
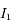 . Que représente cette quantité ?
. Que représente cette quantité ?
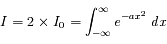
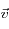 et
et 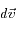 est notée
est notée 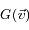 . Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une
. Cette probabilité ne dépend pas de la position ni du temps, car le gaz est en équilibre. Si on fait l'hypothèse que la vitesse est isotrope (qui est vérifiée au sommet d'une 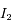 et
et 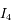 de l'exercice précédent.
de l'exercice précédent.
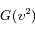 à l'aide des intégrales gaussiennes.
à l'aide des intégrales gaussiennes.
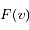 , densité de probabilité pour le module de la vitesse.
, densité de probabilité pour le module de la vitesse.
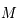 et de rayon
et de rayon 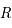 .
.
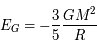 .
.
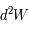 d'une couronne sphérique d'épaisseur
d'une couronne sphérique d'épaisseur 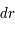 .
.
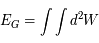 , en prenant les bornes d'intégration adéquates.
, en prenant les bornes d'intégration adéquates.
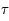 du Soleil sur ses seules ressources gravitationnelles. On rappelle que la luminosité (puissance totale rayonnée) du Soleil est
du Soleil sur ses seules ressources gravitationnelles. On rappelle que la luminosité (puissance totale rayonnée) du Soleil est 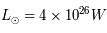 , sa masse
, sa masse 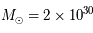 kg et son rayon
kg et son rayon 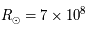 m.
m.
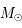 est convertie en hélium et que la luminosité
est convertie en hélium et que la luminosité 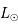 reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie
reste constante. Le rendement de la réaction hydrogène -> hélium est de 0.7%, et on rappelle la relation d'équivalence masse-énergie 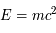 .
.
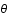 et
et 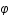 sont choisis comme nuls. On peut donc simplifier la métrique:
sont choisis comme nuls. On peut donc simplifier la métrique:
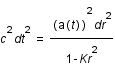 soit
soit 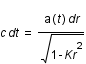 .
.
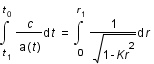
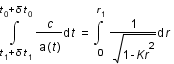
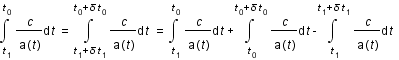
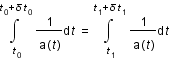
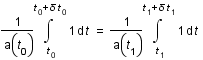
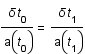
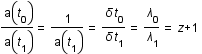
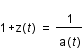
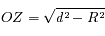 . On en déduit que:
. On en déduit que:
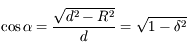 .
.
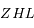 rectangle en
rectangle en 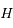 on a:
on a:
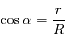 .
On en déduit que:
.
On en déduit que:
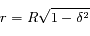 .
.
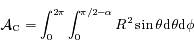 ,
où
,
où 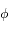 est l'angle
est l'angle 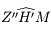 et
et 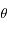 l'angle
l'angle 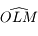 avec
avec 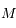 un point de la calotte,
un point de la calotte, 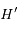 son projeté orthogonal sur la droite
son projeté orthogonal sur la droite 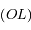 et
et 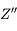 le point de la droite
le point de la droite 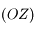 dont la projection orthogonale sur
dont la projection orthogonale sur 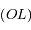 est
est 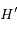 .
.
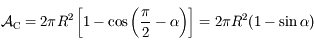 .
C'est-à-dire:
.
C'est-à-dire:
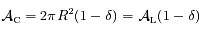 .
.
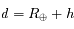 , ainsi
, ainsi 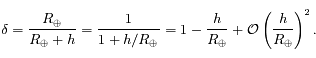 Ainsi
Ainsi 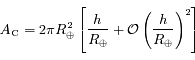 .
.
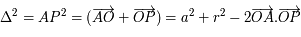
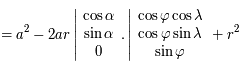
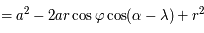
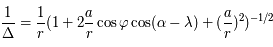
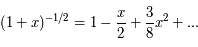
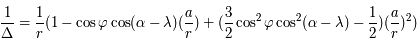
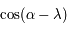 , intégré entre
, intégré entre 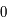 et
et 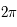 , est nul.
, est nul.
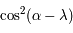 , la valeur de l'intégrale est
, la valeur de l'intégrale est 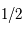 (il suffit de linéariser).
(il suffit de linéariser).
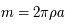 (masse totale de l'anneau) et en notant
(masse totale de l'anneau) et en notant 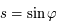 , on obtient:
, on obtient:
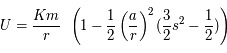
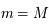 , puis en identifiant les 2 expressions, on obtient
, puis en identifiant les 2 expressions, on obtient 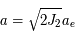 . Ce qui donne 297 km.
. Ce qui donne 297 km.
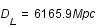
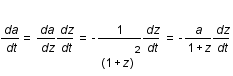
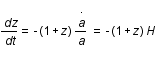
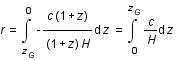
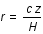 donc
donc 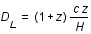 .
.
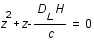 .
.
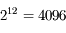 niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou
niveaux. Ces niveaux sont appelés ADU (Analog-to-Digital Units), DN (Digital Numbers) ou 
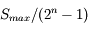
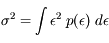
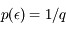 dans l'intervalle [-q/2, q/2]
dans l'intervalle [-q/2, q/2]
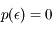 ailleurs
ailleurs

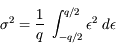
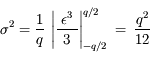
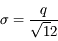 ou encore
ou encore 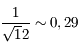 bits.
bits.
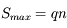 . En rapportant au signal moyen, on trouve :
. En rapportant au signal moyen, on trouve :
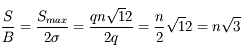

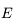 s'écrit comme un produit de fonctions ou de composition de fonctions qui sont de classe
s'écrit comme un produit de fonctions ou de composition de fonctions qui sont de classe 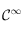 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation21.png) , donc
, donc 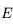 est aussi de
classe classe
est aussi de
classe classe 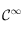 sur
sur ![]0,+\infty[](../pages_int-gen/equations_int-gen/equation24.png) . Le signe s'optient de la même manière, en considérant le signe de chaque fonction intervenant dans le calcul de
. Le signe s'optient de la même manière, en considérant le signe de chaque fonction intervenant dans le calcul de 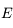 sur cet intervalle.
sur cet intervalle.
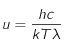 .Ainsi
.Ainsi 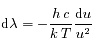 , et en substituant dans l'expression de
, et en substituant dans l'expression de 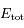 on obtient:
on obtient:
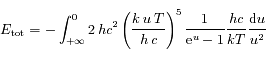 ,
,
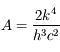 .
.
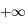 l'intégrande est équivalente à
l'intégrande est équivalente à 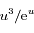 , dont l'intégrale converge en
, dont l'intégrale converge en 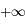 puisque l'exponentielle l'emporte sur tout polynôme;
puisque l'exponentielle l'emporte sur tout polynôme; 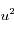 , dont l'intégrale converge 0
, dont l'intégrale converge 0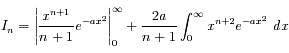
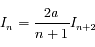
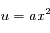 on trouve :
on trouve :
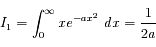
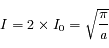
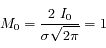 (normalisation de la densité de probabilité).
(normalisation de la densité de probabilité).
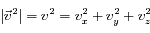
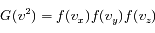
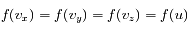 Soit :
Soit : 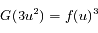
![G(v_x^2+v_y^2+v_z^2) = \left[G(3v_x^2) G(3v_y^2) G(3v_z^2)\right]^{1/3}](../pages_int-gen/equations_int-gen/equation66.png)
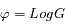 :
:
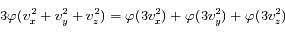
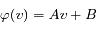
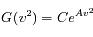
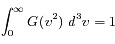
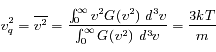
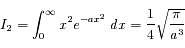
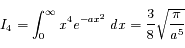
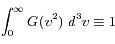
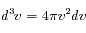 en coordonnées sphériques. Ceci donne :
en coordonnées sphériques. Ceci donne :
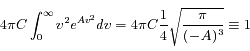
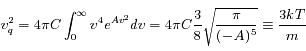
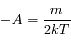 d'où
d'où 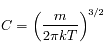
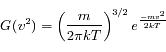
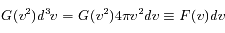
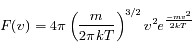

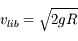 ).
).
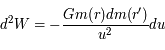
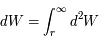
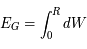
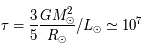 ans.
ans.
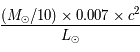 = 10 milliards d'années.
= 10 milliards d'années.
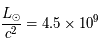 kg/s.
kg/s.
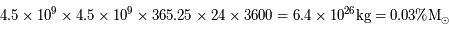 .
.