Auteur: S. Renner
Date de création: 8 avril 2009
Dans le système solaire, on trouve plusieurs exemples de configurations où des petits satellites co-orbitaux sont en orbite autour d'un corps central (planète) beaucoup plus massif. Dans le système de Saturne, les satellites Hélène et Pollux sont en libration autour des points de Lagrange 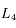 et
et 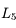 de Dioné. De même, Télesto et Calypso sont respectivement au point
de Dioné. De même, Télesto et Calypso sont respectivement au point 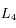 et
et 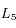 de Téthys. D'autre part, les satellites co-orbitaux Janus et Epiméthée ont des orbites en fer à cheval (cf. figure des points de Lagrange) autour
de leur point
de Téthys. D'autre part, les satellites co-orbitaux Janus et Epiméthée ont des orbites en fer à cheval (cf. figure des points de Lagrange) autour
de leur point 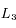 mutuel.
mutuel.
Dans un autre contexte, la présence de 4 arcs de matière (des "morceaux" d'anneau) autour de Neptune pourrait s'expliquer par l'existence de satellites co-orbitaux (non découverts) qui confineraient la poussière observée de l'anneau formant les arcs.
Le but ici est de redémontrer des résultats généraux sur les configurations stationnaires (planes) de 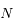 satellites co-orbitaux, en orbite autour
d'une planète beaucoup plus massive (problème à
satellites co-orbitaux, en orbite autour
d'une planète beaucoup plus massive (problème à 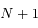 corps, plan). Ces résultats généralisent le problème des points de Lagrange et sont extraits de Renner, S. & Sicardy, B., Celestial Mechanics and Dynamical Astronomy, 88, 397-414, 2004.
corps, plan). Ces résultats généralisent le problème des points de Lagrange et sont extraits de Renner, S. & Sicardy, B., Celestial Mechanics and Dynamical Astronomy, 88, 397-414, 2004.
Plus précisément, on va montrer que l'existence de solutions stationnaires planes pour le problème à 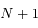 corps dépend de la parité de
corps dépend de la parité de 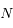 . Plus précisément, si
. Plus précisément, si 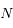 est impair, et pour une configuration angulaire donnée, il existe toujours un ensemble de masses (positives ou négatives) qui réalise un équilibre! Pour
est impair, et pour une configuration angulaire donnée, il existe toujours un ensemble de masses (positives ou négatives) qui réalise un équilibre! Pour 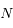 pair au contraire, il n'y a à priori pas de combinaison de masses qui réalise un équilibre, pour des séparations angulaires données entre les satellites.
pair au contraire, il n'y a à priori pas de combinaison de masses qui réalise un équilibre, pour des séparations angulaires données entre les satellites.
Auteur: S. Renner
 Equilibres de satellites co-orbitaux
Equilibres de satellites co-orbitaux
Difficulté : ☆☆
Temps : 2h30
On considère 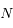 satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note
satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note 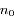 la vitesse angulaire moyenne et
la vitesse angulaire moyenne et 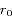 le rayon orbital moyen des satellites.
le rayon orbital moyen des satellites.
On suppose le problème plan, et on se place dans un repère centré sur M et tournant à la vitesse angulaire 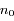 .
.
Le mouvement de chaque satellite est décrit par les coordonnées 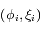 ,
, 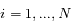 , où
, où 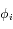 est la longitude du satellite i par rapport à une longitude de référence arbitraire, et
est la longitude du satellite i par rapport à une longitude de référence arbitraire, et 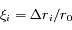 l'excursion radiale relative du satellite par rapport au rayon moyen
l'excursion radiale relative du satellite par rapport au rayon moyen 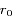 (voir figure ci-dessous).
(voir figure ci-dessous).
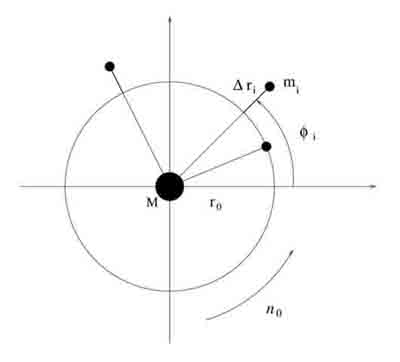
Notations pour la dynamique des satellites co-orbitaux (cf. texte).
On peut montrer que la dynamique de chaque satellite est régie par le système d'équations différentielles suivant :
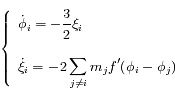
avec
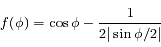 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation23.png) ,
, 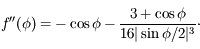
Question 1)
Ecrire les deux équations algébriques donnant les points fixes du système.
Question 2)
Que signifie la première relation?
Question 3)
La seconde relation correspond en fait à 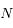 équations linéaires des masses. Ecrire ce système sous forme matricielle. On note
équations linéaires des masses. Ecrire ce système sous forme matricielle. On note 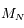 la matrice obtenue.
la matrice obtenue.
Question 4)
Que peut-on dire de la matrice 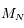 ?
?
Question 5)
Trouver les points d'équilibre dans le cas 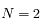 .
.
Question 7)
On suppose que 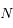 est pair. Déterminer le rang de la matrice
est pair. Déterminer le rang de la matrice 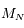 , et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
, et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
Question 8)
Dans le cas où 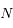 est pair, quelle propriété doit vérifier la matrice
est pair, quelle propriété doit vérifier la matrice 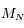 pour pouvoir obtenir des solutions non-triviales
pour pouvoir obtenir des solutions non-triviales 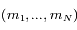 ?
?
Question 9)
Vérifier les deux questions précédentes avec le cas 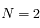 .
.
 En savoir plus
En savoir plus
Les équations du mouvement sont donc:
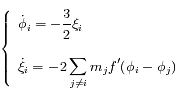
avec
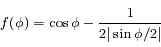 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation111.png) ,
, 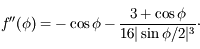
Pour établir ces équations, on a fait les hypothèses suivantes:
- chaque satellite a une masse négligeable devant celle du corps central : quelque soit
 ,
,  , où
, où  est la masse du
est la masse du 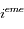 satellite
satellite
- l'excentricité des satellites est supposée nulle
- les satellites ne s'approchent pas trop de leurs rayons de Hill mutuels, définis par
![r_H = r_0 \cdot \left[\left(m_i + m_j\right)/3M\right]^{1/3}](../pages_syst-lin/equations_syst-lin/equation117.png) . Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange
. Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange 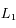 et
et 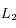 dans le cas N=2).
dans le cas N=2).
- pour simplifier et sans perte de généralité on a choisi
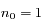 ,
, 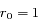 et
et 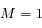
La première équation n'est rien d'autre que la vitesse keplerienne différentielle de chaque satellite par rapport à l'orbite de référence de rayon 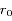 . La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
. La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
La fonction 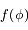 est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde
est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde 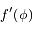 et
et 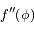 .
.
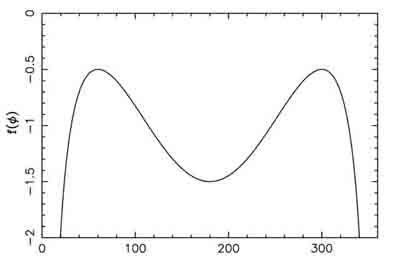
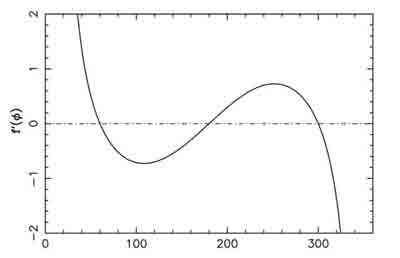
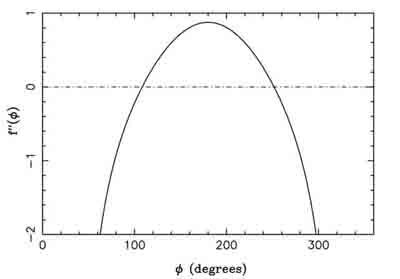
La fonction
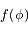
, décrivant le potentiel créé par un satellite sur une particule co-orbitale, avec ses dérivées première et seconde
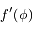
et
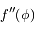
.
Puisque 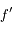 est impaire, il est facile de montrer d'après les équations du mouvement que
est impaire, il est facile de montrer d'après les équations du mouvement que 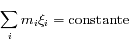 . Le rayon de référence
. Le rayon de référence 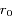 étant arbitraire, il peut être choisi de telle manière que
étant arbitraire, il peut être choisi de telle manière que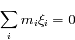 , sans perte de généralité. Ainsi le système possède les intégrales premières suivantes :
, sans perte de généralité. Ainsi le système possède les intégrales premières suivantes :
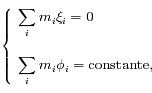
qui résultent de la conservation du moment cinétique total. Cette conservation résulte elle-même de l'invariance par rotation du problème. Il existe une autre intégrale première :
![J= \sum_{i} m_i \left[ - {3 \over 4} \xi_i^2 + \sum_{j \neq i} m_j f(\phi_i - \phi_j) \right]](../pages_syst-lin/equations_syst-lin/equation135.png)
Elle exprime la conservation de l'énergie dans le repère tournant, et est appelée constante de Jacobi.
Auteur: Marc Fouchard
 exposants de Lyapunov
exposants de Lyapunov
Difficulté : ☆☆☆
Temps : 1h30
Question 3)
Montrer que 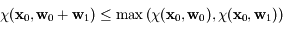 .
.
Question 5)
En déduire qu'il existe au plus 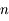 exposants de Lyapunov distincts pour une trajectoire donnée.
exposants de Lyapunov distincts pour une trajectoire donnée.
Procéder par l'absurde en supposant 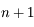 exposants de Lyapunov distincts.
exposants de Lyapunov distincts.
-
Question 1
Solution :
Les points fixes du système sont donnés par :
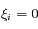 ,
,
et
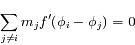
pour tout  .
.
-
Question 2
Solution :
La première équation signifie qu'en configuration stationnaire les  satellites co-orbitaux ont le même rayon orbital. Dans le problème exact, cela est seulement vrai à l'ordre 0 en
satellites co-orbitaux ont le même rayon orbital. Dans le problème exact, cela est seulement vrai à l'ordre 0 en 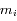 . Les petites corrections d'ordre
. Les petites corrections d'ordre 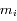 sont ici négligées.
sont ici négligées.
-
Question 3
Solution :
La seconde équation fait intervenir les séparations angulaires entre les satellites et peut s'écrire sous forme matricielle. On définit 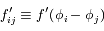 . La fonction
. La fonction 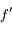 étant impaire, on obtient:
étant impaire, on obtient:
![\left [ \begin{array}{ccccc} 0 & f'_{12} & \cdots & \cdots & f'_{1N} \\ - f'_{12} & 0 & f'_{23} & \cdots & f'_{2N} \\ \vdots & & 0 & & \\ \vdots & & & \ddots & \\ - f'_{1N} & & & & 0 \end{array} \right] \cdot \left [ \begin{array}{ccccc} m_1 \\ m_2 \\ \vdots \\ \vdots \\ m_N \end{array} \right] \equiv M_N \cdot \left [ \begin{array}{ccccc} m_1 \\ m_2 \\ \vdots \\ \vdots \\ m_N \end{array} \right] = 0_{{\mathbb R}^N}](../pages_syst-lin/equations_syst-lin/equation35.png)
-
Question 4
Solution :
La matrice 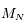 définie ci-dessus est antisymétrique. Elle ne dépend que des longitudes
définie ci-dessus est antisymétrique. Elle ne dépend que des longitudes 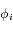 , via les coefficients
, via les coefficients 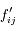 .
.
-
Question 5
Solution :
Avec 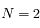 , la condition d'équilibre s'écrit
, la condition d'équilibre s'écrit
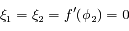 ,
,
c'est-à-dire
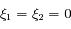 et
et 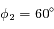 ,
, 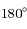 ou
ou 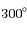 .
.
Les points d'équilibre sont respectivement les points de Lagrange 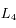 ,
, 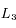 et
et 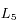 .
.
-
Question 6
Solution :
Puisque 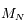 est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
Par conséquent, pour des angles 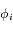 donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre
donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre 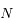 de satellites.
de satellites.
Si N est impair, 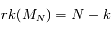 avec
avec 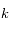 impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs
impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs 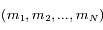 pour laquelle la configuration est stationnaire: étant données par exemple
pour laquelle la configuration est stationnaire: étant données par exemple 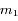 ,
, 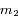 , ...,
, ..., 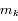 , le système linéaire admet une et une seule solution
, le système linéaire admet une et une seule solution 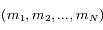 .
.
-
Question 7
Solution :
Si 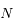 est pair, le rang de
est pair, le rang de 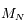 est généralement
est généralement 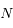 : étant donnée une configuration angulaire arbitraire
: étant donnée une configuration angulaire arbitraire 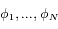 , il n'existe pas en général de solutions non-triviales
, il n'existe pas en général de solutions non-triviales 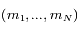 pour lesquelles
pour lesquelles 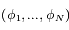 est un équilibre.
est un équilibre.
-
Question 8
Solution :
On doit tout d'abord annuler le déterminant de la matrice, 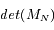 , afin de trouver des solutions non-triviales.
, afin de trouver des solutions non-triviales.
-
Question 9
Aide :
Dans le cas 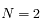 , seuls les points de Lagrange
, seuls les points de Lagrange 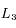 ,
, 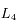 et
et 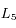 sont des points d'équilibre. Deux satellites à par exemple
sont des points d'équilibre. Deux satellites à par exemple 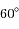 l'un de l'autre sont stationnaires quelque soit le choix arbitraire des masses
l'un de l'autre sont stationnaires quelque soit le choix arbitraire des masses 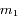 et
et 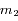 .
.
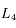 et
et 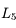 de Dioné. De même, Télesto et Calypso sont respectivement au point
de Dioné. De même, Télesto et Calypso sont respectivement au point 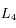 et
et 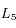 de Téthys. D'autre part, les satellites co-orbitaux Janus et Epiméthée ont des orbites en fer à cheval (cf. figure des points de Lagrange) autour
de leur point
de Téthys. D'autre part, les satellites co-orbitaux Janus et Epiméthée ont des orbites en fer à cheval (cf. figure des points de Lagrange) autour
de leur point 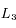 mutuel.
mutuel.
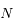 satellites co-orbitaux, en orbite autour
d'une planète beaucoup plus massive (problème à
satellites co-orbitaux, en orbite autour
d'une planète beaucoup plus massive (problème à 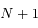 corps, plan). Ces résultats généralisent le problème des points de Lagrange et sont extraits de Renner, S. & Sicardy, B., Celestial Mechanics and Dynamical Astronomy, 88, 397-414, 2004.
corps, plan). Ces résultats généralisent le problème des points de Lagrange et sont extraits de Renner, S. & Sicardy, B., Celestial Mechanics and Dynamical Astronomy, 88, 397-414, 2004.
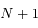 corps dépend de la parité de
corps dépend de la parité de 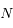 . Plus précisément, si
. Plus précisément, si 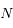 est impair, et pour une configuration angulaire donnée, il existe toujours un ensemble de masses (positives ou négatives) qui réalise un équilibre! Pour
est impair, et pour une configuration angulaire donnée, il existe toujours un ensemble de masses (positives ou négatives) qui réalise un équilibre! Pour 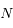 pair au contraire, il n'y a à priori pas de combinaison de masses qui réalise un équilibre, pour des séparations angulaires données entre les satellites.
pair au contraire, il n'y a à priori pas de combinaison de masses qui réalise un équilibre, pour des séparations angulaires données entre les satellites.
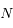 satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note
satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note 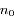 la vitesse angulaire moyenne et
la vitesse angulaire moyenne et 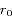 le rayon orbital moyen des satellites.
le rayon orbital moyen des satellites.
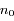 .
.
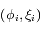 ,
, 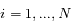 , où
, où 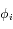 est la longitude du satellite i par rapport à une longitude de référence arbitraire, et
est la longitude du satellite i par rapport à une longitude de référence arbitraire, et 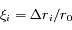 l'excursion radiale relative du satellite par rapport au rayon moyen
l'excursion radiale relative du satellite par rapport au rayon moyen 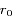 (voir figure ci-dessous).
(voir figure ci-dessous).

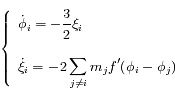
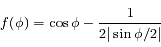 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation23.png) ,
, 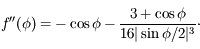
 équations linéaires des masses. Ecrire ce système sous forme matricielle. On note
équations linéaires des masses. Ecrire ce système sous forme matricielle. On note 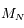 la matrice obtenue.
la matrice obtenue.
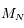 ?
?
 .
.
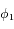 ,...,
,...,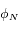 tels que
tels que 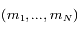 soit solution de l'équation matricielle, avec
soit solution de l'équation matricielle, avec 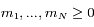 . Il est évidemment impossible de résoudre cette équation analytiquement pour
. Il est évidemment impossible de résoudre cette équation analytiquement pour 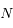 quelconque. On peut néanmoins déduire des propriétés générales sur les solutions.
quelconque. On peut néanmoins déduire des propriétés générales sur les solutions.
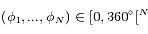 tel que
tel que 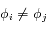 pour tout
pour tout 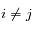 (f' n'est pas définie en 0).
(f' n'est pas définie en 0).
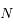 est impair. Déterminer le rang de la matrice
est impair. Déterminer le rang de la matrice 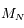 , puis en déduire qu'il existe une famille à
, puis en déduire qu'il existe une famille à 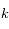 paramètres, avec
paramètres, avec 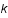 entier impair, de vecteurs
entier impair, de vecteurs 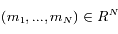 pour laquelle
pour laquelle 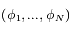 est une configuration stationnaire.
est une configuration stationnaire.
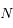 est pair. Déterminer le rang de la matrice
est pair. Déterminer le rang de la matrice 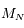 , et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
, et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
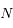 est pair, quelle propriété doit vérifier la matrice
est pair, quelle propriété doit vérifier la matrice 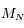 pour pouvoir obtenir des solutions non-triviales
pour pouvoir obtenir des solutions non-triviales 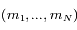 ?
?
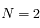 .
.
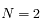 , seuls les points de Lagrange
, seuls les points de Lagrange 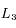 ,
, 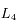 et
et 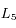 sont des points d'équilibre. Deux satellites à par exemple
sont des points d'équilibre. Deux satellites à par exemple 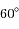 l'un de l'autre sont stationnaires quelque soit le choix arbitraire des masses
l'un de l'autre sont stationnaires quelque soit le choix arbitraire des masses 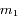 et
et 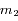 .
.
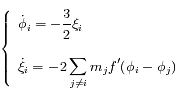
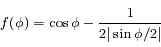 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation111.png) ,
, 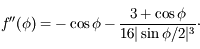
 ,
, 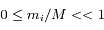 , où
, où  est la masse du
est la masse du 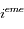 satellite
satellite![r_H = r_0 \cdot \left[\left(m_i + m_j\right)/3M\right]^{1/3}](../pages_syst-lin/equations_syst-lin/equation117.png) . Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange
. Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange 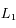 et
et 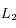 dans le cas N=2).
dans le cas N=2).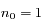 ,
, 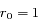 et
et 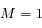
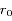 . La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
. La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
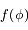 est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde
est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde 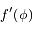 et
et 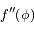 .
.



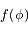 , décrivant le potentiel créé par un satellite sur une particule co-orbitale, avec ses dérivées première et seconde
, décrivant le potentiel créé par un satellite sur une particule co-orbitale, avec ses dérivées première et seconde 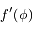 et
et 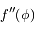 .
.
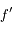 est impaire, il est facile de montrer d'après les équations du mouvement que
est impaire, il est facile de montrer d'après les équations du mouvement que 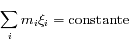 . Le rayon de référence
. Le rayon de référence 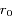 étant arbitraire, il peut être choisi de telle manière que
étant arbitraire, il peut être choisi de telle manière que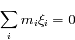 , sans perte de généralité. Ainsi le système possède les
, sans perte de généralité. Ainsi le système possède les 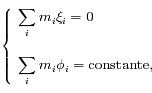
![J= \sum_{i} m_i \left[ - {3 \over 4} \xi_i^2 + \sum_{j \neq i} m_j f(\phi_i - \phi_j) \right]](../pages_syst-lin/equations_syst-lin/equation135.png)
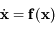 ,
,
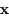 est un vecteur de dimension
est un vecteur de dimension 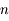 , et
, et 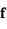 une fonction vectorielle de dimension
une fonction vectorielle de dimension 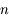 continue et dérivable.
continue et dérivable.
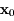 suivant le vecteur
suivant le vecteur 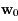 la quantité:
la quantité:
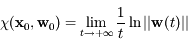 ,
,
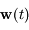 est solution de l'équation différentielle:
est solution de l'équation différentielle:
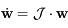 ,
,
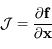 est le
est le 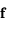 .
.
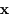 . Les vecteurs
. Les vecteurs 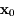 et
et 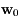 sont les conditions initiales de ces équations différentielles.
sont les conditions initiales de ces équations différentielles.
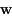 le vecteur tangent à la trajectoire. Il évolue dans un espace appelé espace tangent qui peut être identifié à
le vecteur tangent à la trajectoire. Il évolue dans un espace appelé espace tangent qui peut être identifié à 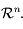
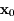 est chaotique ou pas.
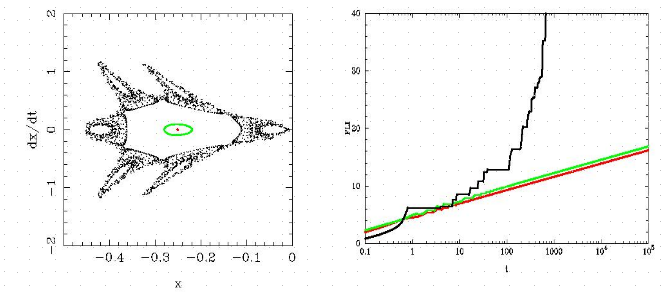
Par exemple sur la figure ci-dessous on peut voir qu'un dérivé des exposants de Lyapunov (Exposant de Lyapunov Rapide) se comporte de manière différente pour une trajectoire régulière (accroisement linéaire) et pour une trajectoire chaotique (accroissement exponentiel).
Dans la suite on va étudier les exposants de Lyapunov associés à la trajectoire passant par
est chaotique ou pas.
Par exemple sur la figure ci-dessous on peut voir qu'un dérivé des exposants de Lyapunov (Exposant de Lyapunov Rapide) se comporte de manière différente pour une trajectoire régulière (accroisement linéaire) et pour une trajectoire chaotique (accroissement exponentiel).
Dans la suite on va étudier les exposants de Lyapunov associés à la trajectoire passant par 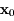 à
à 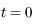 et démontrer quelques propriétés élémentaires de ces exposants, en particulier leur similarité avec le spectre des valeurs propres d'en endomorphisme.
et démontrer quelques propriétés élémentaires de ces exposants, en particulier leur similarité avec le spectre des valeurs propres d'en endomorphisme.
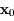 et de période
et de période 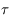 . Ainsi après une période on a
. Ainsi après une période on a 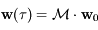 , où
, où 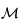 est une matrice carrée de dimension
est une matrice carrée de dimension 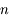 , et pour
, et pour 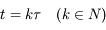 on a
on a 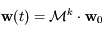 . Montrer que si
. Montrer que si 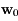 est un vecteur propre de la matrice
est un vecteur propre de la matrice 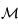 associé à la valeur propre
associé à la valeur propre 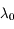 alors:
alors:
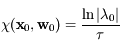
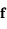 . Dans le cas général la matrice
. Dans le cas général la matrice 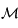 n'existe pas. Cependant on va voir qu'on peut définir un spectre d'exposants de Lypunov associé au Jacobien de
n'existe pas. Cependant on va voir qu'on peut définir un spectre d'exposants de Lypunov associé au Jacobien de 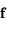 ayant certaines similarités avec le spectre des valeurs propres d'une matrice.
ayant certaines similarités avec le spectre des valeurs propres d'une matrice.
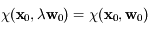 , pour
, pour 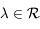 .
.
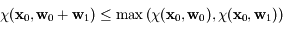 .
.
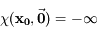 , montrer que pour tout
, montrer que pour tout 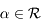 , l'ensemble
, l'ensemble 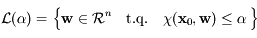 , forme un sous-espace vectoriel de
, forme un sous-espace vectoriel de 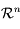 .
.
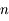 exposants de Lyapunov distincts pour une trajectoire donnée.
exposants de Lyapunov distincts pour une trajectoire donnée.
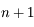 exposants de Lyapunov distincts.
exposants de Lyapunov distincts.
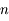 exposants distincts et tels que
exposants distincts et tels que 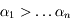 , avec
, avec 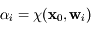 , alors les vecteurs
, alors les vecteurs 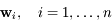 forment une base
de
forment une base
de 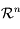 .
Dans la pratique, on ne connait pas les vecteurs permettant de déterminer les exposants de Lyapunov. Mais si on prend un vecteur au hasard il apartiendra à
.
Dans la pratique, on ne connait pas les vecteurs permettant de déterminer les exposants de Lyapunov. Mais si on prend un vecteur au hasard il apartiendra à 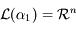 mais peu probablement à
mais peu probablement à 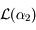 . En effet pour qu'il y appartienne il faudrait que la composante de ce vecteur suivant
. En effet pour qu'il y appartienne il faudrait que la composante de ce vecteur suivant 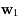 soit égale à zéro. Lors d'un tirage au hasard cette probabilité est nulle.
soit égale à zéro. Lors d'un tirage au hasard cette probabilité est nulle.
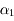 . Il permet de savoir si une orbite est stable ou chaotique. En effet dans le cas d'une orbite stable la norme du vecteur tangent va très probablement augmenter linéairement avec le temps, ainsi
. Il permet de savoir si une orbite est stable ou chaotique. En effet dans le cas d'une orbite stable la norme du vecteur tangent va très probablement augmenter linéairement avec le temps, ainsi 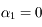 , alors que dans le cas chaotique elle va augmenter très probablement exponentiellement avec le temps, ainsi
, alors que dans le cas chaotique elle va augmenter très probablement exponentiellement avec le temps, ainsi 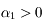 .
.
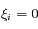 ,
,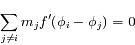
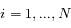 .
.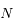 satellites co-orbitaux ont le même rayon orbital. Dans le problème exact, cela est seulement vrai à l'ordre 0 en
satellites co-orbitaux ont le même rayon orbital. Dans le problème exact, cela est seulement vrai à l'ordre 0 en 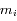 . Les petites corrections d'ordre
. Les petites corrections d'ordre 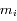 sont ici négligées.
sont ici négligées.
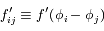 . La fonction
. La fonction 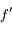 étant impaire, on obtient:
étant impaire, on obtient:
![\left [ \begin{array}{ccccc} 0 & f'_{12} & \cdots & \cdots & f'_{1N} \\ - f'_{12} & 0 & f'_{23} & \cdots & f'_{2N} \\ \vdots & & 0 & & \\ \vdots & & & \ddots & \\ - f'_{1N} & & & & 0 \end{array} \right] \cdot \left [ \begin{array}{ccccc} m_1 \\ m_2 \\ \vdots \\ \vdots \\ m_N \end{array} \right] \equiv M_N \cdot \left [ \begin{array}{ccccc} m_1 \\ m_2 \\ \vdots \\ \vdots \\ m_N \end{array} \right] = 0_{{\mathbb R}^N}](../pages_syst-lin/equations_syst-lin/equation35.png)
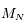 définie ci-dessus est antisymétrique. Elle ne dépend que des longitudes
définie ci-dessus est antisymétrique. Elle ne dépend que des longitudes 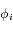 , via les coefficients
, via les coefficients 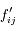 .
.
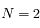 , la condition d'équilibre s'écrit
, la condition d'équilibre s'écrit
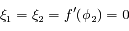 ,
,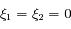 et
et 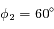 ,
, 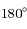 ou
ou 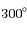 .
.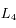 ,
, 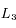 et
et 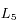 .
.
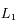 et
et 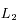 n'apparaissent pas. Cela résulte des
n'apparaissent pas. Cela résulte des 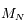 est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
est antisymétrique, son rang est pair. C'est un résultat classique d'algèbre linéaire, non redémontré ici.
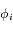 donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre
donnés, l'existence de solutions non-triviales (positives ou négatives) du système linéaire va dépendre de la parité du nombre 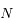 de satellites.
de satellites.
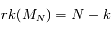 avec
avec 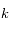 impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs
impair. Ainsi, étant données des séparations angulaires arbitraires et non-nulles entre les satellites, il existe une famille à k paramètres de vecteurs 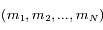 pour laquelle la configuration est stationnaire: étant données par exemple
pour laquelle la configuration est stationnaire: étant données par exemple 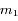 ,
, 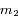 , ...,
, ..., 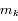 , le système linéaire admet une et une seule solution
, le système linéaire admet une et une seule solution 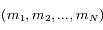 .
.
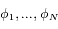 à un sous-ensemble de
à un sous-ensemble de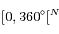 .
.
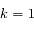 "presque partout". Dans l'espace des
"presque partout". Dans l'espace des 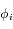 , l'ensemble pour lequel le rang de
, l'ensemble pour lequel le rang de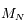 est
est 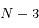 ,
, 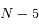 ,..., est de mesure nulle.
Ainsi étant donnée par exemple
,..., est de mesure nulle.
Ainsi étant donnée par exemple 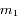 , il y aura une et une seule solution
, il y aura une et une seule solution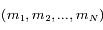 pour laquelle
pour laquelle 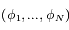 est une configuration d'équilibre.
est une configuration d'équilibre.
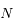 est pair, le rang de
est pair, le rang de 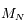 est généralement
est généralement 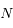 : étant donnée une configuration angulaire arbitraire
: étant donnée une configuration angulaire arbitraire 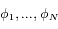 , il n'existe pas en général de solutions non-triviales
, il n'existe pas en général de solutions non-triviales 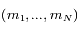 pour lesquelles
pour lesquelles 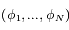 est un équilibre.
est un équilibre.
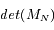 , afin de trouver des solutions non-triviales.
, afin de trouver des solutions non-triviales.
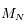 sera "presque partout"
sera "presque partout"  sur
sur 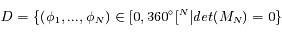 . Dans ce cas, il existe une famille à 2 paramètres de vecteurs pour lesquels la configuration est stationnaire.
. Dans ce cas, il existe une famille à 2 paramètres de vecteurs pour lesquels la configuration est stationnaire.
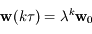 . Ainsi:
. Ainsi:
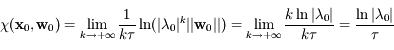 .
.
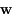 est linéaire. On en déduit que si
est linéaire. On en déduit que si 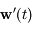 désigne l'évolution de
désigne l'évolution de 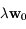 et
et 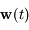 l'évolution de
l'évolution de 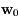 alors on a
alors on a 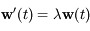 . Ainsi on a :
. Ainsi on a :
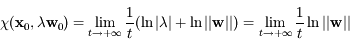
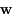 , si on note
, si on note 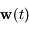 et
et 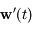 les évolutions respectives de
les évolutions respectives de 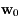 et
et 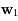 on a:
on a:
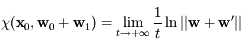 .
.
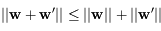 . Ainsi, la fonction logarithme étant croissante, on a:
. Ainsi, la fonction logarithme étant croissante, on a:
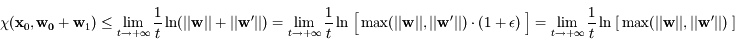
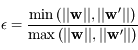 , ainsi
, ainsi 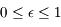 ce qui permet d'éliminer le facteur
ce qui permet d'éliminer le facteur 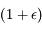 lors du passage à la limite (division par
lors du passage à la limite (division par  ).
).
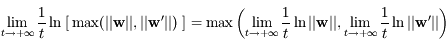 ,
,
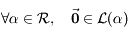 . En tant que sous-espace d'un espace vectoriel, il suffit de montrer donc de montrer que
. En tant que sous-espace d'un espace vectoriel, il suffit de montrer donc de montrer que  est stable par combinaison linéaire. Ceci est une conséquance immédiate des deux questions précédentes.
est stable par combinaison linéaire. Ceci est une conséquance immédiate des deux questions précédentes.
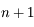 . soit
. soit 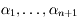 les
les 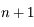 exposants de Lyapunov, tels que
exposants de Lyapunov, tels que 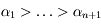 . Par définition on a
. Par définition on a 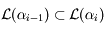 avec
avec 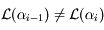 .
Ainsi
.
Ainsi 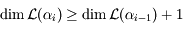 . Soit
. Soit 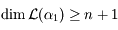 . Or
. Or 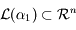 qui est de dimension
qui est de dimension 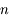 , donc il ne peut y avoir
, donc il ne peut y avoir 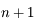 exposants de Lyapunov distincts.
exposants de Lyapunov distincts.