

En savoir plus: Configurations d'équilibre de satellites co-orbitaux |
Les équations du mouvement sont donc:
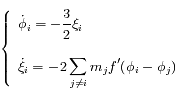
avec
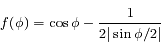 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation111.png) ,
, 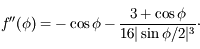
Pour établir ces équations, on a fait les hypothèses suivantes:
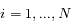 ,
, 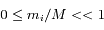 , où
, où 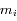 est la masse du
est la masse du 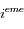 satellite
satellite![r_H = r_0 \cdot \left[\left(m_i + m_j\right)/3M\right]^{1/3}](../pages_syst-lin/equations_syst-lin/equation117.png) . Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange
. Ainsi on évite tout mouvement chaotique, et les satellites restent co-orbitaux. On ne considère pas en particulier les points stationnaires alignés avec le satellite et la planète (comme les points de Lagrange 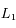 et
et 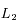 dans le cas N=2).
dans le cas N=2).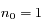 ,
, 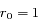 et
et 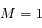
La première équation n'est rien d'autre que la vitesse keplerienne différentielle de chaque satellite par rapport à l'orbite de référence de rayon 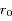 . La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
. La seconde équation contient, sous forme dérivée, tous les termes résultant des interactions gravitationnelles mutuelles entre les satellites.
La fonction 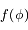 est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde
est la somme des potentiels direct et indirect exercé par un satellite donné sur les autres co-orbitaux. C'est une fonction paire, et son graphe est tracé ci-dessous avec ses dérivées première et seconde 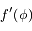 et
et 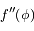 .
.
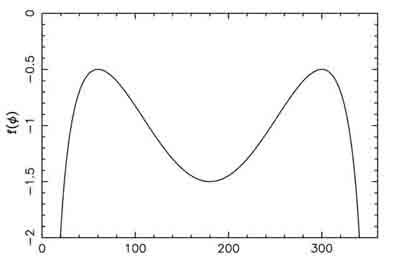
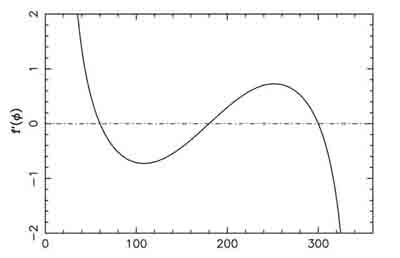
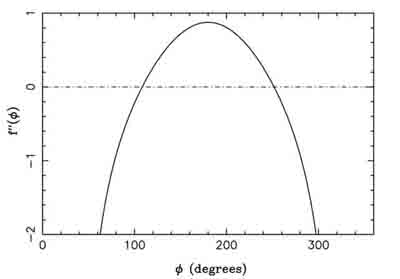
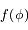 , décrivant le potentiel créé par un satellite sur une particule co-orbitale, avec ses dérivées première et seconde
, décrivant le potentiel créé par un satellite sur une particule co-orbitale, avec ses dérivées première et seconde 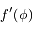 et
et 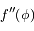 .
.
Puisque 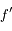 est impaire, il est facile de montrer d'après les équations du mouvement que
est impaire, il est facile de montrer d'après les équations du mouvement que 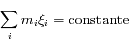 . Le rayon de référence
. Le rayon de référence 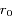 étant arbitraire, il peut être choisi de telle manière que
étant arbitraire, il peut être choisi de telle manière que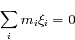 , sans perte de généralité. Ainsi le système possède les intégrales premières suivantes :
, sans perte de généralité. Ainsi le système possède les intégrales premières suivantes :
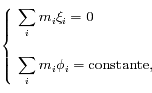
qui résultent de la conservation du moment cinétique total. Cette conservation résulte elle-même de l'invariance par rotation du problème. Il existe une autre intégrale première :
![J= \sum_{i} m_i \left[ - {3 \over 4} \xi_i^2 + \sum_{j \neq i} m_j f(\phi_i - \phi_j) \right]](../pages_syst-lin/equations_syst-lin/equation135.png)
Elle exprime la conservation de l'énergie dans le repère tournant, et est appelée constante de Jacobi.