

Ex: Configurations d'équilibre de satellites co-orbitaux |
Difficulté : ☆☆ Temps : 2h30
On considère 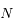 satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note
satellites co-orbitaux en orbite autour d'un corps central supposé ponctuel de masse M. On note 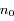 la vitesse angulaire moyenne et
la vitesse angulaire moyenne et 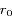 le rayon orbital moyen des satellites.
le rayon orbital moyen des satellites.
On suppose le problème plan, et on se place dans un repère centré sur M et tournant à la vitesse angulaire 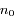 .
.
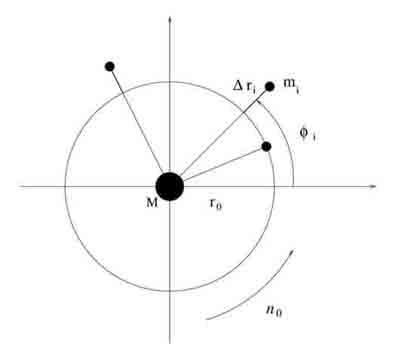
Le mouvement de chaque satellite est décrit par les coordonnées 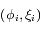 ,
, 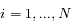 , où
, où 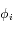 est la longitude du satellite i par rapport à une longitude de référence arbitraire, et
est la longitude du satellite i par rapport à une longitude de référence arbitraire, et 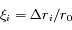 l'excursion radiale relative du satellite par rapport au rayon moyen
l'excursion radiale relative du satellite par rapport au rayon moyen 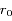 (voir figure ci-dessous).
(voir figure ci-dessous).
On peut montrer que la dynamique de chaque satellite est régie par le système d'équations différentielles suivant :
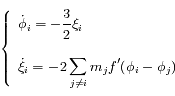
avec
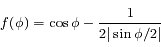 ,
, ![f'(\phi)= \sin \phi \left[ -1 + {1 \over 8|\sin \phi/2|^3} \right]](../pages_syst-lin/equations_syst-lin/equation23.png) ,
, 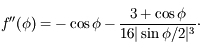
Ecrire les deux équations algébriques donnant les points fixes du système.
Que signifie la première relation?
La seconde relation correspond en fait à 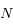 équations linéaires des masses. Ecrire ce système sous forme matricielle. On note
équations linéaires des masses. Ecrire ce système sous forme matricielle. On note 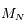 la matrice obtenue.
la matrice obtenue.
Que peut-on dire de la matrice 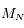 ?
?
Trouver les points d'équilibre dans le cas 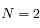 .
.
On cherche à trouver tous les angles 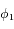 ,...,
,...,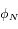 tels que
tels que 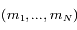 soit solution de l'équation matricielle, avec
soit solution de l'équation matricielle, avec 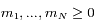 . Il est évidemment impossible de résoudre cette équation analytiquement pour
. Il est évidemment impossible de résoudre cette équation analytiquement pour 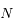 quelconque. On peut néanmoins déduire des propriétés générales sur les solutions.
quelconque. On peut néanmoins déduire des propriétés générales sur les solutions.
soit 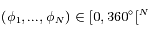 tel que
tel que 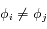 pour tout
pour tout 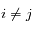 (f' n'est pas définie en 0).
(f' n'est pas définie en 0).
On suppose que 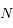 est impair. Déterminer le rang de la matrice
est impair. Déterminer le rang de la matrice 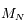 , puis en déduire qu'il existe une famille à
, puis en déduire qu'il existe une famille à 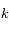 paramètres, avec
paramètres, avec 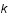 entier impair, de vecteurs
entier impair, de vecteurs 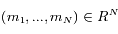 pour laquelle
pour laquelle 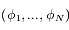 est une configuration stationnaire.
est une configuration stationnaire.
On suppose que 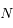 est pair. Déterminer le rang de la matrice
est pair. Déterminer le rang de la matrice 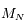 , et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
, et en déduire qu'en général il n'existe pas de famille de vecteurs qui réalise un équilibre.
Dans le cas où 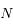 est pair, quelle propriété doit vérifier la matrice
est pair, quelle propriété doit vérifier la matrice 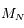 pour pouvoir obtenir des solutions non-triviales
pour pouvoir obtenir des solutions non-triviales 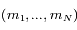 ?
?
Vérifier les deux questions précédentes avec le cas 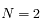 .
.