Exposants de Lyapunov |
Auteur: Marc Fouchard
Date de création: 4 avril 2011
On considère le système dynamique suivant:
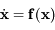 ,
,
où 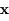 est un vecteur de dimension
est un vecteur de dimension 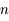 , et
, et 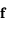 une fonction vectorielle de dimension
une fonction vectorielle de dimension 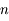 continue et dérivable.
continue et dérivable.
On appelle exposant de Lyapunov en 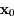 suivant le vecteur
suivant le vecteur 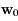 la quantité:
la quantité:
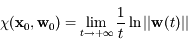 ,
,
où 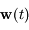 est solution de l'équation différentielle:
est solution de l'équation différentielle:
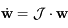 ,
,
avec 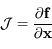 est le Jacobien de
est le Jacobien de 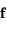 .
.
Cette équation, appelée équation variationnelle, est associée à l'équation différentielle décrivant l'évolution de 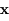 . Les vecteurs
. Les vecteurs 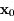 et
et 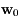 sont les conditions initiales de ces équations différentielles.
sont les conditions initiales de ces équations différentielles.
On appelle généralement le vecteur 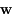 le vecteur tangent à la trajectoire. Il évolue dans un espace appelé espace tangent qui peut être identifié à
le vecteur tangent à la trajectoire. Il évolue dans un espace appelé espace tangent qui peut être identifié à 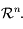
Les exposants de Lyapunov permettent de savoir si la trajectoire passant par 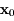 est chaotique ou pas.
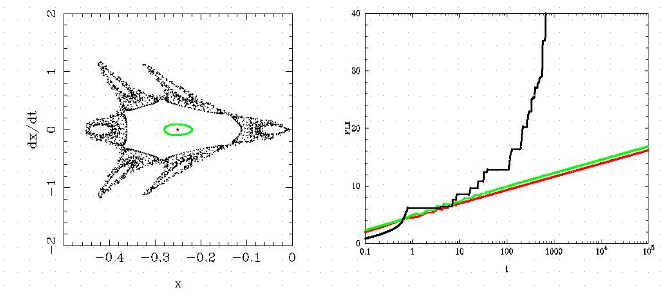
Par exemple sur la figure ci-dessous on peut voir qu'un dérivé des exposants de Lyapunov (Exposant de Lyapunov Rapide) se comporte de manière différente pour une trajectoire régulière (accroisement linéaire) et pour une trajectoire chaotique (accroissement exponentiel).
Dans la suite on va étudier les exposants de Lyapunov associés à la trajectoire passant par
est chaotique ou pas.
Par exemple sur la figure ci-dessous on peut voir qu'un dérivé des exposants de Lyapunov (Exposant de Lyapunov Rapide) se comporte de manière différente pour une trajectoire régulière (accroisement linéaire) et pour une trajectoire chaotique (accroissement exponentiel).
Dans la suite on va étudier les exposants de Lyapunov associés à la trajectoire passant par 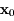 à
à 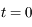 et démontrer quelques propriétés élémentaires de ces exposants, en particulier leur similarité avec le spectre des valeurs propres d'en endomorphisme.
et démontrer quelques propriétés élémentaires de ces exposants, en particulier leur similarité avec le spectre des valeurs propres d'en endomorphisme.