Formation de H2 sur un grain interstellaire
Auteurs:
Safwan Aljbaae, Romain Hascoet, Olivier Maloyer, Vivien Parmentier, Jean-Claude Passy
Date de création :
13/01/2009
Table des matières
Introduction
L'objet de cet applet Java est d'étudier la formation de H2 dans le milieu interstellaire.
La molécule de H2 est indispensable au démarrage de nombreuses réactions chimique interstellaires. Or les conditions de pression et de température dans le milieu interstellaire ne permettent pas d'avoir formation de H2 par collision directe de deux atomes d'hydrogène. En réalité il est nécessaire d'avoir présence de grains de poussière interstellaires qui servent de catalyseurs dans la réaction :
Un atome d'hydrogène se déplace librement dans le milieu interstellaire puis est adsorbé sur un grain de poussière. Sous l'effet de l'agitation thermique, ils se déplace de sites en sites jusqu'à rencontrer un autre atome d'hydrogène avec lequel il a une certaine probabilité de se recombiner formant ainsi une molécule de H2 qui s'évapore dans le milieu interstellaire.
-
Objectifs
-
Cet applet Java simule l'arrivée des atomes d'hydrogène sur le grain et leur déplacement jusqu'à formation et évaporation d'une molécule de H2.
Champ
Milieu interstellaire
Explications
Explications théoriques
On a vu que la formation de H2 est expliquée par la rencontre de deux atomes d'hydrogènes sur un grain de poussière du milieu interstellaire.
L'arrivée de ces atomes sur le grain, leur déplacement et l'évaporation des molécules de H2 ainsi formées sont soumises à des lois complexes qui devraient rigoureusement prendre en compte la nature du grain, la présence d'impuretés, l'energie cinétique des atomes, etc ...
On se bornera ici à un modèle simplifié où seules les caractéristiques essentielles à la compréhension générale du phénomène sont prises en compte :
Pour commencer, on ne considère qu'un seul grain modélisé par un ensemble de sites sur lesquels peuvent être adsorbés les atomes d'hydrogène. (on entend indifféremment par site, le site de l'adsorption -qui est ponctuel- ainsi que la cellule de Voronoï associée à ce site. (Cf.
Triangulation de Delaunay sur une sphère )
Chacun des atomes d'hydrogène se déplaçant de sites en sites sur le grain, il s'agit donc en fait d'effectuer une marche aléatoire de ces particules sur un réseau dont les noeuds sont les sites du grain.
On considérera que les passages d'un site à un autre seront toujours de type "plus proches voisins" (c'est-à-dire qu'un atome ne peut partir d'un site que pour aller vers un autre qui est en contact avec ce dernier)
De plus, on considérera qu'une molécule de H2 se forme dès que deux atomes d'hydrogène se retrouvent sur le même site.
En réalité il existe différents types de formation des molécules de H2 :
- Processus de Langmuir-Hinshelwood : les atomes de H2 sont attachés au grain par physisorption (liaisons de Van Der Waals) et peuvent se déplacer à sa surface même à une température faible. La formation d'une molécule de H2 est rendue possible lors de la rencontre de deux de ces atomes sur le même site
- Processus de Eley-Rideal : un atome de H2 est lié à un site du grain par chimisorption (liaison forte) et une molécule de H2 ne peut être formée que par arrivée sur le même site d'un atome d'hydrogène suffisamment énergétique (en pratique un atome venant directement du milieu interstellaire).
- Processus de Harris-Kasemo : processus intermédiaire entre les deux précédents.
Nous considérerons le cas simple où toutes les évaporations sont identiques.
De même, par soucis de simplicité, la lois d'arrivée des atomes sur le grain ainsi que la loi qui gère les déplacements des atomes d'hydrogène d'un site à l'autre sont chacune prises poissonnienne avec un temps caractéristique qui dépend des paramètres d'entrée :
La statistique de passage d'un site à un autre pour un atome d'hydrogène adsorbé sur le grain est lié entre autres à :
- la température du grain (une forte agitation thermique favorise le mouvement des atomes sur la paroi du grain.)
- la surface du site sur lequel est l'atome (on comprend que plus le site est large et donc isolé d'autre sites, moins la particule a de chances de se déplacer sur un autre site.)
- La composition du grain (on suppose pour simplifier que le grain est homogène)
Au final, le temps caractéristisque de déplacement des atomes est donné par :
où
et L est la taille caractristique d'un site.
En plus des atomes déjà sur le grain, s'ajoutent d'autres atomes d'hydrogène provenant du milieu interstellaire dont la fréquence d'adsorption est liée à la densité de H et à la température du milieu interstellaire. La constante de temps d'un tel phénomène est :
où
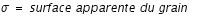
et
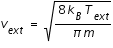
est la vitesse moyenne des atomes d'hydrogène dans le milieu interstellaire
Plusieurs types de grain sont envisagées :
- Des grains toriques dont les sites forment un pavage carré régulier (il s'agit d'un plan avec des conditions aux limites périodiques)
- Des grains sphériques dont les sites sont répartis aléatoirement avec une loi de distribution uniforme.
Mode d'emploi de l'applet
Introduction
Après réglages des paramètres, la simulation peut être lancée :
On peut voir alors une représentation du grain (modélisé par ses sites).
De plus, on observe l'arrivée, le déplacement et l'évaporation des atomes sur chacun des sites.
Remarque :
Afin d'être sur que le modèle ne s'arrête pas, un minimum de deux particules est maintenu en permanence sur le grain.
Paramètres utilises
Les paramètres à régler sont essentiellement ceux qui interviennent dans le déplacement d'un particule d'un site à l'autre, c'est-à-dire : la température, la taille du grain (ou son nombre de sites) ainsi que les paramètres réglant l'arrivée de nouveaux atomes sur le grain, c'est-à-dire la densité en H du milieu interstellaire.
Affichage
On peut souhaiter afficher deux choses :
- le déplacement des atomes sur les sites.
- la fonction de répartition de la durée de vie d'un atome d'hydrogène sur le grain. (par durée de vie on entend le temps qu'a passé la particule sur le grain entre son arrivée depuis le milieu interstellaire et son départ suite à la formation puis l'évaporation d'une molécule de H2)
Selon que l'on choisit un grain torique ou sphérique, l'affichage du déplacement des particules différera :
- Dans le premier cas, on affichera simplement une grille carrée dont les points d'intersections représenteront les sites du grain.
Il faut comprendre que dans cette représentation le point d'un bord est en contact avec le point correspondant du bord opposé.
- Si l'on choisit un grain sphérique, on utilisera, pour représenter les sites, la méthode des cellules de Voronoï (Cf. Triangulation de Delaunay sur une sphère )
Les sites du grain sont modélisés par de points noirs. Les atomes se déplacant de sites en sites sont représentés par des points rouges.
Les particules se déplacent les une après les autres, pour pouvoir plus simplement suivre le déplacement d'un site à l'autre des particules, on affiche un point vert sur le site où va se déplacer le prochain atome et un point bleu sur le site que vient de quitter une particule.
Interface de base
Interface de base

Au lancement de l'applet il apparait une interface à plusieurs boutons qui permettent de régler les paramètres qui influent sur la formation de H2 : c'est-à-dire les deux températures (celle du milieu interstellaire et celle du grain, égales à l'équilibre thermique), la densité en H du milieu interstellaire, la taille du grain et la densité de sites d'adsorption sur le grain.
Une fois les paramètres initiaux réglés, les trois boutons du bas permettent de choisir quel type de résultat visualiser :
- "Affichage" : Ce mode permet de voir chaque particule (en rouge) se déplacer sur les sites d'adsorption (en noir) du grain. Le site sur lequel va se déplacer le prochain atome est représenté en vert et sa dernière position est marquée en bleu.
- "Nombre de particules sur le grain" : Cette option affiche un graphique représentant le nombre de paricules sur le grain en fonction du temps. Ceci permet de voir dans quel régime de peuplement du grain on se trouve : fort taux d'occupation (et dans ce cas le processus d'Eley-Rideal est dominant) ou faible taux d'occupation (on a alors en majorité des processus de type Langmuir-Hinshelwood)
- "Logarithme de la fonction de répartition" : Il s'agit de regarder la loi que suit le temps de vie d'une particule c'est-à-dire le temps qu'a passé la particule sur le grain entre son arrivée depuis le milieu interstellaire et son départ suite à la formation puis l'évaporation d'une molécule de H2.
Comme on sait que la fonction de répartition de cette variable dans le cas d'un plan infini est une loi exponentielle, on trace le logarithme de la fonction de répartition. On peut ainsi vérifier que l'on a une droite dans le cas d'un grain torique suffisamment grand et voir l'écart à cette loi dans le cas d'un grain sphérique dans différentes situations.
Remarque :
Si la case "rafraichissement rapide" est cochée l'option "Affichage" n'a plus grand sens : on ne voit alors l'emplacement des particules seulement à chaque évaporation.
Remarque :
De même si "rafraichissement rapide" n'est pas coché, l'option "Logarithme de la fonction de répartition" ne doit pas être prise.
Remarque :
Un dernier bouton permet de régler le temps de pause entre deux affichages. Ceci permet de ralentir l'affichage du programme afin de mieux voir l'évolution des particules sur le grain.
Liste des paramètres d'entrée de l'applet
-
titre : Nombre intial de particules
label : initialParticleNumber
Le nombre initial de particules présent sur le grain. Il doit être égal à 1 au minimum.
-
titre : Geometrie du grain
label : maillage
Ce paramètre sert à choisir sur quel type de grain on veut effectuer la simulation : torique ou sphérique.
Le modèle torique est donné à titre pédagogique, pour comprendre le fonctionnement de l'applet. Il sert aussi à comparer les résultats obtenus sur un grain sphérique à sites aléatoirement répartis avec ceux, plus connus et plus simples, obtenus sur un plan infini.
Valeurs possibles :
-
titre : Densité de site sur le grain
label : densisite
unités : 1/µm²
Ce paramètre fixe la densité de H dans le milieu interstellaire, ce qui influe sur la fréquence d'arrivée des atomes d'hydrogène sur le grain. (Plus le milieu est dense, plus la fréquence d'arrivée sur le grain est élevée)
-
titre : Temperature
label : temperature
unités : K
Ce paramètre fixe la température du milieu interstellaire, ce qui influe sur la probabilité d'arrivée des atomes d'hydrogènes sur le grain. (Une forte température a tendance à faire arriver plus rapidement des atomes d'hydrogène sur le grain)
-
titre : Température du grain
label : tgrain
unités : K
Ce paramètre fixe la température du grain, ce qui influe sur la probabilité de passage d'un site à l'autre du grain pour un atome d'hydrogène. (Une forte température a tendance a faire se déplacer plus fréquemment une particule d'un site à l'autre)
-
titre : Taille
label : diameter
unités : µm
Diamètre moyen du grain.
-
titre : Densité du milieu
label : density
unités : particules/cm3
Densité du milieu interstellaire.
-
titre : Pause entre deux affichages
label : pause
unités : centième de seconde
Permet de ralentir l'affichage du programme afin de mieux voir l'évolution des particules sur le grain.
Est inutile si la case "rafraichissement rapide" est cochée.
-
titre : rafraichissement rapide (ie uniquement lors d'une évaporation)
label : affichage
Cocher lorsque vous ne vous interessez pas aux positions exactes des particules à tout instants. Obligatoire pour visualiser la fonction de répartition. A éviter pour visualiser l'affichage.
Liste des paramètres de sortie de l'applet
-
label : nombredepoints
-
label : nombre
-
label : carte
-
label : tevap
-
titre : Nombre de particules sur le grain
label : particlenumber
-
label : time
Exemple d'utilisation
Option "Affichage"
Affichage des particules se mouvant sur un grain sphérique (représentation projective)
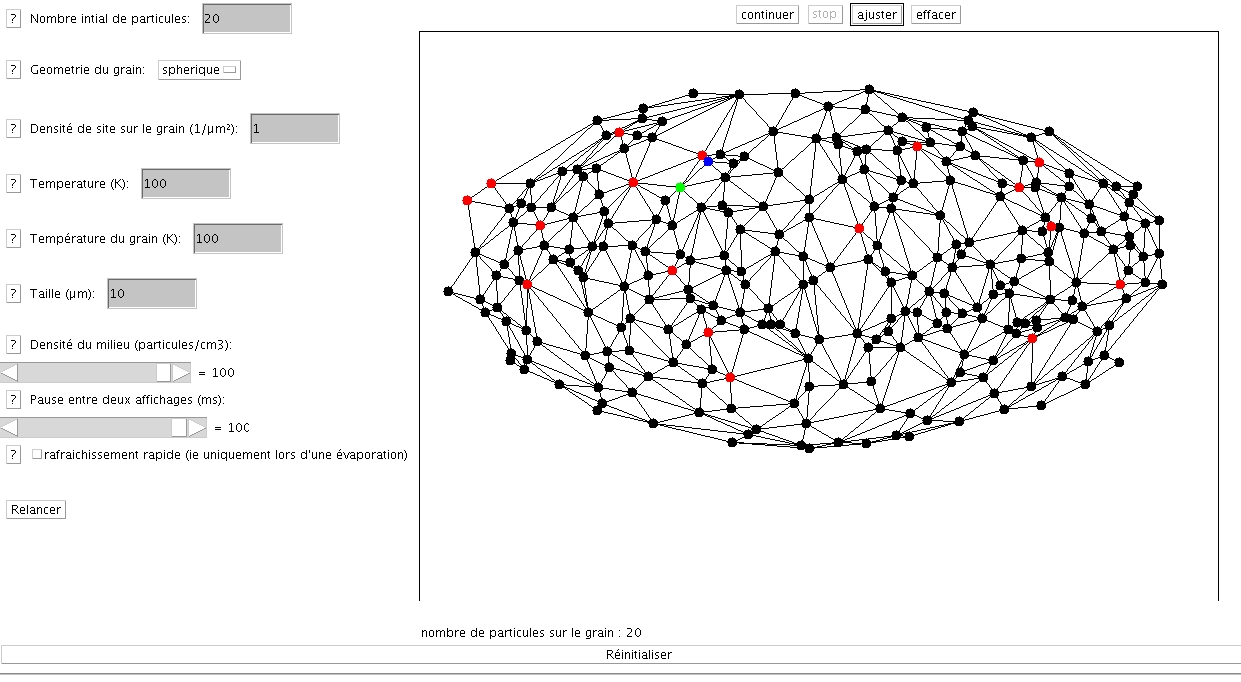
Ce mode permet de voir chaque particule (en rouge) se déplacer sur les sites d'adsorption (en noir) du grain. Le site sur lequel va se déplacer le prochain atome est représenté en vert et le site duquel il part est marqué en bleu.
Option "Logarithme de la fonction de répartition"
Affichage du logarithme de la fonction de répartition dans le cas d'un grain torique
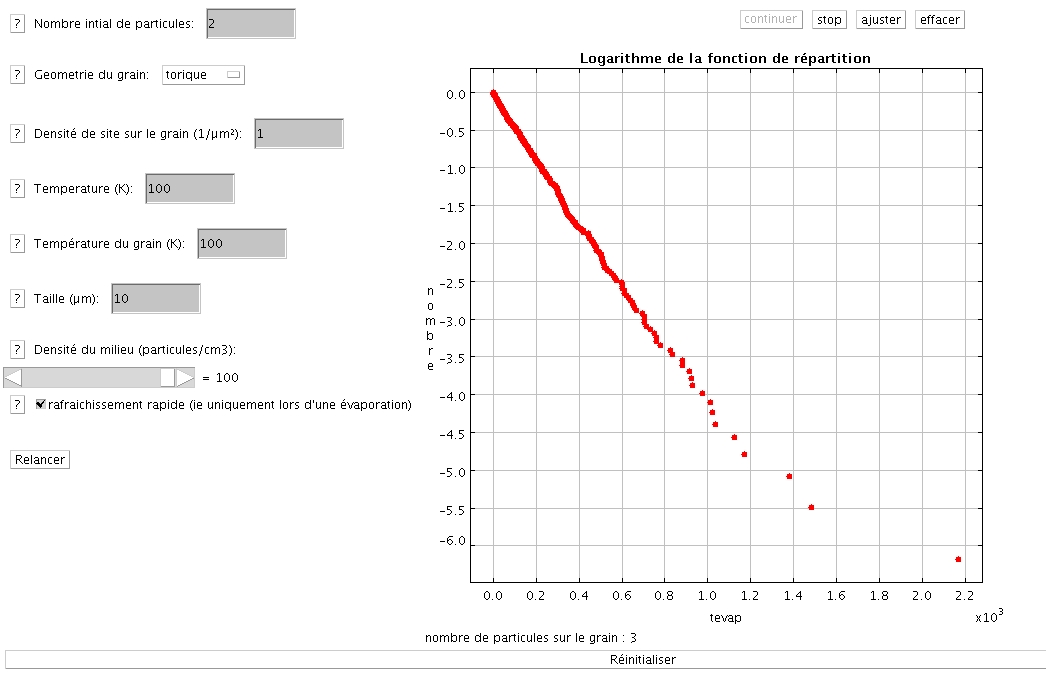
La marche aléatoire sur les noeuds d'un graphe carré est bien connue, la fonction de répartition du temps de rencontre entre deux particules suit une loi exponentielle. Ici on a pris un grain torique assez gros pour qu'il puisse être considéré comme un plan infini.
Puisque l'on trace le logarithme de la fonction de répartition, il est normal que l'on observe une droite.
Les points qui se trouvent à droite du graphique (et qui correspondent donc à des grands temps de parcours avant une collision sur le grain) sont des évènements rares et ont alors des positions erratiques. Ces points s'alignent d'autant plus avec la droite observée que l'on fait durer longtemps la simulation.
Option "Nombre de particules sur le grain"
Affichage du nombre de grains en fonction du temps dans le cas d'une température forte
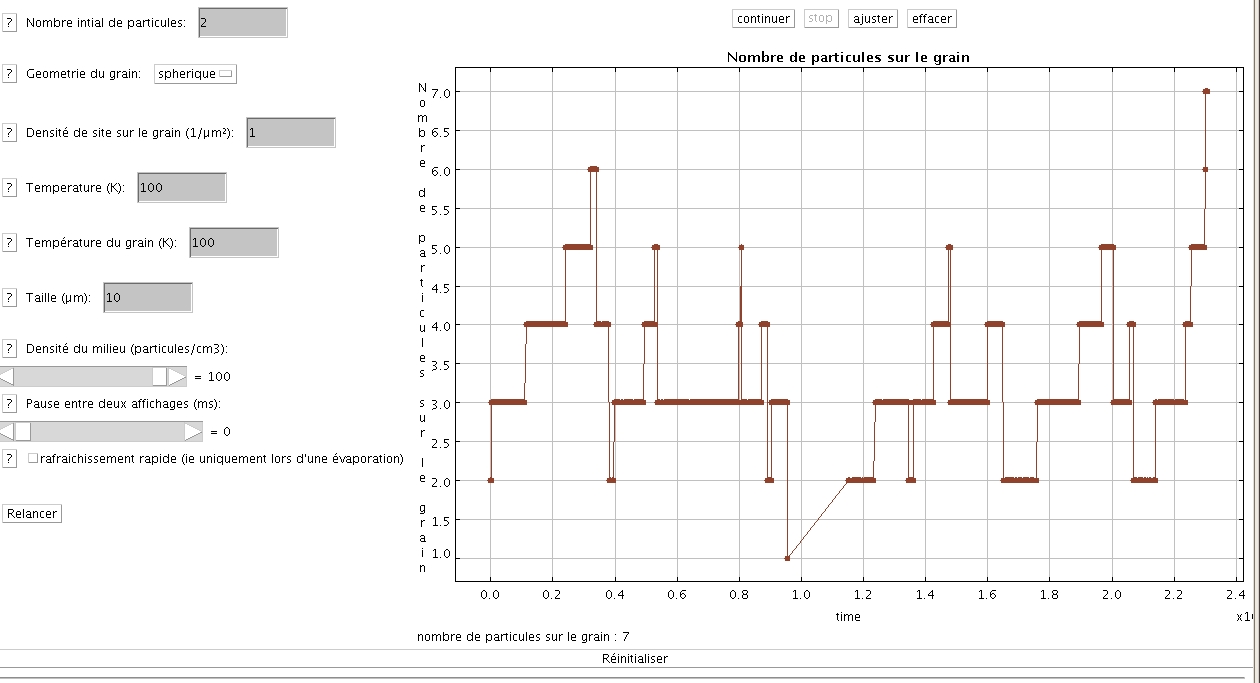
Affichage du nombre de grains en fonction du temps dans le cas d'une température faible
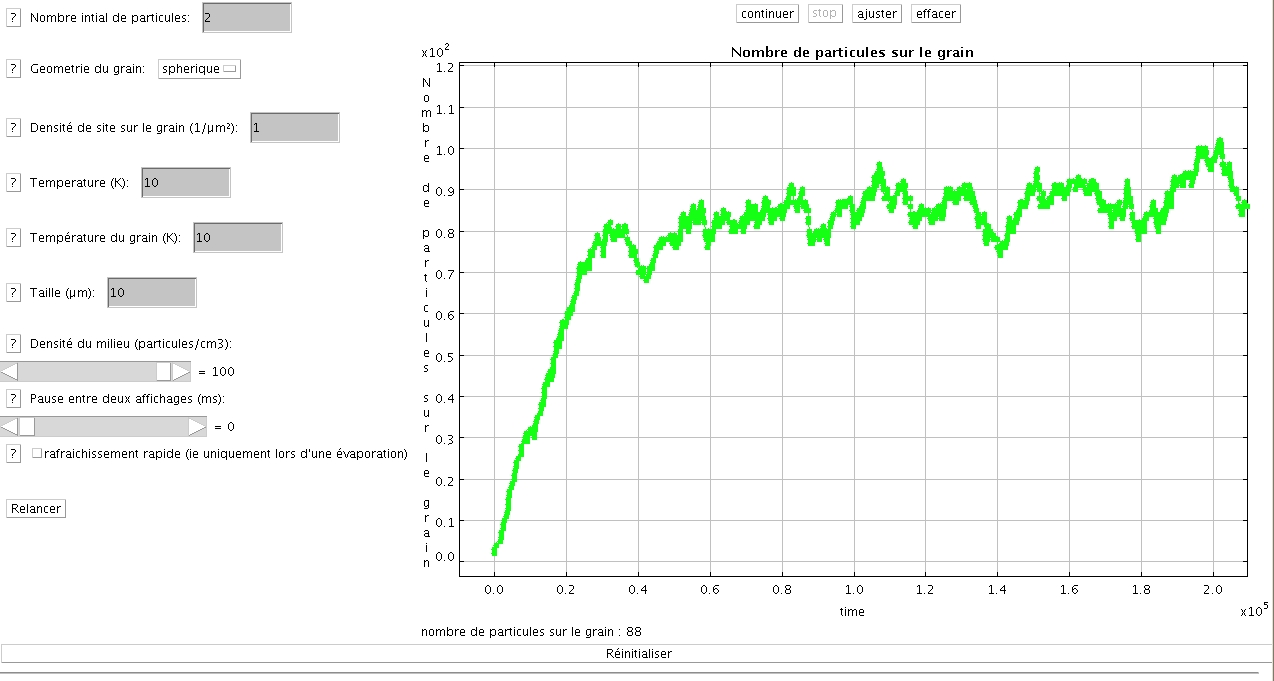
Cette option affiche un graphique représentant le nombre de paricules sur le grain en fonction du temps. Ceci permet de voir dans quel régime de peuplement du grain on se trouve : fort taux d'occupation (et dans ce cas le processus d'Eley-Rideal est dominant) ou faible taux d'occupation (on a alors en majorité des processus de type Langmuir-Hinshelwood)
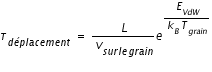
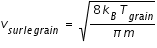
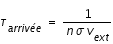
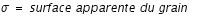
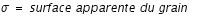
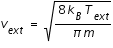 est la vitesse moyenne des atomes d'hydrogène dans le milieu interstellaire
est la vitesse moyenne des atomes d'hydrogène dans le milieu interstellaire
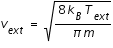 est la vitesse moyenne des atomes d'hydrogène dans le milieu interstellaire
est la vitesse moyenne des atomes d'hydrogène dans le milieu interstellaire




