Introduction
Les rayons lumineux du Soleil (ou potentiellement de la Lune) interagissent avec les cristaux présents dans la haude atmosphère pour former des halos atmosphériques. La forme de ceux-ci est dictée par les caractéristiques de ces cristaux, en particulier leur forme et orientation. L'observation es halos permet ainsi d'obtenir des informations très précises sur les caractéristiques des cristaux présents en haute altitude, et par là même, sur les conditions qui y règnent afin d'avoir permis la création de certains types de cristaux et non d'autres ou certaines orientations privilégiées.
Cette applet permet de visualiser des halos observables en fonction de divers paramètres tels que la hauteur du Soleil au dessus de l'horizon ou les caractéristiques des cristaux (forme, orientations, etc.) et de voir ainsi comment ces paramètres influent sur les halos.
Outre l'étude de l'atmosphère terrestre, des images de halos qui seraient prises par des sondes donneraient de précieux renseignements sur l'atmosphère de la planète explorée. Une telle étude était au programme de la sonde Mars Polar Lander en 1999, mais celle-ci n'a pas atteint la surface de la planète.
Présentation
Cet applet a pour but de simuler des halos atmosphériques, en calculant l'interaction de milliers de rayons lumineux avec des cristaux de formes prédéterminées, possédant des orientations aléatoires ou potentiellement privilégiées selon un axe donné.
Algorithme
Conventions de notation
Dans la section suivante, on notera :
-
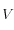
la position de l'observateur (choisi comme centre du repère)
-
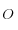
le centre de la Terre
-
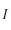
la position du cristal dans le nuage
-
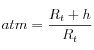
, est le rapport entre la distance des nuages au centre de la Terre et le rayon de celle-ci. Les paramètres
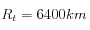
et
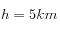
ont été choisis.
-
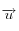
le vecteur unitaire des rayons arrivant du Soleil. Il est défini en fonction de la hauteur de celui-ci au dessus de l'horizon
-
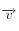
la ligne de visée de l'observateur, soit la direction du ciel dans laquelle il regarde
-
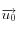
le vecteur unitaire de direction
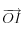
conventions

Interaction avec le cristal
Le cristal choisi est généré une fois pour toutes au lancement de la simulation.
Son orientation est choisie aléatoirement (en tenant compte des contraintes imposées sur l'orientation des axes principaux) et imposée au cristal.
Un rayon de couleur et de point source aléatoires est généré (actuellement, seules 3 couleurs sont prises en compte, correspondant grossièrement aux couleurs rouge verte et bleue d'un écran, soit 650nm, 510nm et 440nm). Les méthodes décrites dans la
documentation de l'applet Refraction et utilisées dans la méthode
vecteur_sortie de la classe Cristal permettent d'obtenir directement l'orientation du rayon après interaction avec le cristal.
Afin de prendre en compte l'orientation des cristaux par rapport au sol, il est nécessaire de tourner le vecteur de sortie d'un angle correspondant à la hauteur du Soleil, on obtient alors le vecteur
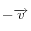
A partir de ceci, on impose que le rayon émergent soit vu par l'observateur, ce qui impose la position
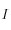
du cristal dans le ciel. Ce point est déterminé par intersection du vecteur de ligne de visée
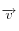
avec la sphère représentant les nuages de cristaux via la formule
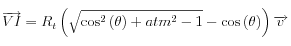
où
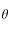
est la distance zénithale de la direction donnée par
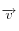
Méthodes de discriminations des rayons
Certains rayons ne sont pas intéressants pour la simulation, d'autres ne sont pas à prendre en compte et enfin, les luminosités qu'il convient de tenir compte dépendent de l'endroit de l'atmosphère où se trouve le cristal (l'éclairement du Soleil n'étant pas uniforme sur la surface de la Terre)
-
Les rayons non déviés sont rejetés : ceux-ci étant nombreux, la luminosité du point central empêcherait de voir les phénomènes peu lumineux recherchés autour.
Le critère de choix utilisé consiste simplement à rejeter les rayons pour lesquels la déviation a été inférieure à
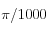
.
-
Les rayons lumineux ayant dû traverser la Terre pour atteindre le cristal ne sont pas physiques et sont donc rejetés.
Le critère de choix est basé sur l'angle
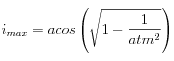
représentant l'angle sous lequel les cristaux "voient" la Terre. L'angle d'arrivée du rayon lumineux par rapport à
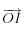
(direction de la verticale du cristal) est l'angle entre
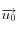
et
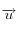
. Si cet angle est supérieur à
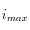
, le rayon doit être rejeté.
représentation de imax
Remarque : dans le programme, on raisonne sur les cosinus des angles en question, pour des raisons pratiques (le produit scalaire donne directement cette grandeur) et parce qu'on en a besoin pour l'étape suivante
-
L'intensité lumineuse des rayons incidents doit varier pour prendre en compte l'éclairement non uniforme du Soleil (il est moins important aux pôles qu'à l'équateur, ou plus généralement, moins important en zone périphérique d'éclairement où le Soleil apparait bas sur l'horizon). Le facteur est donné par le cosinus de l'angle entre le rayon incident de direction
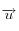
et le vecteur
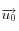
déterminant le point éclairé dans l'atmosphère. La grandeur recherché est donc simplement le produit scalaire des deux vecteurs, qui est prise comme telle en tant qu'intensité lumineuse.
Projection
Pour terminer, la direction du rayon vu par l'observateur est projeté en utilisant la
projection orthographique, en tenant compte des paramètres de hauteur et azimut du centre de la fenêtre d'affichage et du zoom choisis par l'utilisateur.
Si la projection de ce rayon arrive dans la fenêtre d'affichage, l'intensité correspondant au rayon considéré est ajouté à l'image
L'affichage
La perception de l'oeil étant logarithmique, c'est le logarithme de l'intensité lumineuse calculée qui est affiché. Ceci permet en outre de faire ressortir les phénomènes peu lumineux pour une meilleure visualisation.
A chaque actualisation, une renormalisation est effectuée afin d'afficher l'image la plus lumineuse possible.
Améliorations possibles
Comme suggéré pour
l'applet Réfraction, il serait intéressant d'ajouter d'autres types de cristaux, et d'autre compositions. En particulier il serait intéressant d'ajouter les indices optiques de l'ammoniac, en prévision desquels a été créé le cristal bipyramidal, et l'ajout de cristaux de glace carbonique, avec les indices associés permettrait de faire des simulations de halos atmosphériques martiens.
Il serait possible d'ajouter divers type de projections (fisheye ...) pour l'affichage en plus de l'orthographique actuellement en place.
Pour plus de réalisme, il serait également possible de prendre en compte les coefficients de Fresnel, ce qui provoquerait l'apparition des phénomènes nécessitant des réflexions internes supplémentaires sans imposer celles-ci, et en respectant les luminosités relatives de certains phénomènes associés. Par exemple, les
parenthélies, les
arcs en ciel primaire et secondaires (l'option actuelle serait cependant également à conserver afin de faire ressortir des effets particulièrement fins au besoin).
On pourrait par ailleurs prendre en compte les réflexions externes, en vue de rendre certains effets optiques comme les piliers du Soleil.
Les paramètres influents sur la formation des halos sont nombreux, et certains sont relativement sensibles.
Les paramètres par défaut de l'applet permettent de visualiser les
halos à 22° et 46°, les plus courramment observés car nécessitant peu de contraintes.
D'autres halos peuvent facilement être simulés en choisissant dans le menu déroulant situé en haut de la liste des paramètres. Les paramètres correspondants seront alors reportés en dessous afin de réaliser la simulation correspondante.
Ces divers paramètres peuvent être modifiés à volonté (chacun d'eux est expliqué ci-dessous) ; pour que la modification soit prise en compte, il est nécessaire de relancer le calcul après chaque changement effectué.
Attention : par défaut la case " réinitialiser " n'est pas cochée (elle l'est par contre dès qu'un choix est effectué dans la liste des paramètres prédéfinis), et dans ce cas, l'image ne sera pas effacée entre chaque calcul.
L'intérêt de cette option est de pouvoir facilement superposer des halos, soit en gardant une position du Soleil fixe et en modifiant le type de cristaux ou leur orientation (voir par exemple les
arcs tangents et le halo à 22° superposés ci-dessous), ou en gardant les paramètres des cristaux inchangés et en modifiant la hauteur du Soleil pour visualiser la modification d'aspect du halo correspondant (voir par exemple
les images du halo circumhorizontal ci-dessous)
Il faut cependant faire attention aux superpositions ainsi effectuées afin qu'elles gardent un sens. Il serait ainsi irréaliste de superposer le halo formé par des cristaux hexagonaux et le Soleil se trouvant à une hauteur de 20° avec celui formé par des gouttes d'eau et le Soleil se trouvant à 50°.
Hauteur du Soleil
La hauteur du Soleil est un paramètre important, puisque certains halos ne sont visibles que lorsque le Soleil se trouve au dessus ou au dessous d'une certaine valeur (les
arcs circumhorizontaux et
circumzénithaux par exemple).
Les halos peuvent également changer de forme de façon très sensible avec ce paramètre (le
halo tangent par exemple). La valeur à entrer est en degrés, 0 correspondant au Soleil au niveau de l'horizon, 90 au Soleil se trouvant au zénith.
Zoom
Ce paramètre permet de choisir la taille de la portion de ciel affichée à l'écran.
Un zoom de 180° correspond à l'affichage de tout le ciel, un nombre plus petit affichera une partie du ciel dont la hauteur en degrés correspond au zoom choisi.
Type d'objet
Le choix du type "d'objet", cristal ou goutte va déterminer la forme du halo. Plusieurs types sont proposés, chacun pouvant avantageusement être visualisé à l'aide de
l'applet Refraction.
-
Le cristal hexagonal est le celui dans lequel l'eau cristallise le plus facilement. Il est à l'origine des halos les plus communément observés.
-
Les cristaux pyramidaux et pyramidaux tronqués ont également une base hexagonale et l'eau cristallise selon ces formes également. Ils sont plus complexes, et forment généralement des halos plus complexes.
-
La goutte sphérique, typiquement la goutte d'eau, a été ajoutée en vue de simuler les arcs en ciel
-
Le cristal bipyramidal est pour le moment inutilisable en tant que tel, dans le sens où c'est la forme d'un cristal d'ammoniac et que les propriétés de ce composé n'ont pas été enregistrées dans cet applet. Il a toutefois été laissé en guise de démonstration.
Facteur de forme
Le facteur de forme correspond grossièrement au rapport hauteur sur largeur du cristal.
Pour une visualisation plus précise des effets de ce paramètre, il peut être utile de se référer à
l'applet Refraction.
Attention : ce paramètre est sans effet sur certains objets comme la goutte sphérique, qui reste sphérique ...
Matériau
Choix du matériau composant l'objet choisi : eau ou glace d'eau.
Il est nécessaire de choisir un matériau compatible avec le type d'objet choisi : une sphère de glace ou un cristal d'eau n'aurait en effet aucun sens.
Réflexions internes
Certains halos sont dus des interactions nécessitant une réflexion interne (partielle) supplémentaire par rapport au chemin que suit majoritairement la lumière.
Pour les
arcs en ciel, une ou deux réflexions internes supplémentaires sont nécessaires par exemple, le trajet direct de la lumière ne causant qu'un halo blanc autour du Soleil.
Le nombre de ces réflexions internes ne doit pas être trop grand : en effet, au delà de 2 ou 3 réflexions partielles, seule une petite fraction de la lumière restera, causant des phénomènes bien trop peu lumineux pour être observables.
Orientation du cristal
L'orientation du cristal est causée par les vents d'altitude et va influer sur les halos observables.
-
Une orientation aléatoire indique que le cristal pourra tourner librement dans toutes les directions.
-
Une orientation avec l'axe principal vertical indique que le cristal pourra tourner librement autour de son axe principal, qui lui restera vertical à de légères variations près (par défaut, un demi degré).
L'axe principal du cristal hexagonal ou pyramidal tronqué est celui passant par les deux faces hexagonales, pour le pyramidal et bipyramidal c'est celui passant par les sommets où les 6 ou 4 faces triangulaires se rejoignent. Cette orientation est plutôt rencontrée dans le cas de cristaux " plats ", donc de facteur de forme petit
-
Une orientation avec l'axe principal horizontal possède les mêmes caractéristiques que précédemment, avec l'axe principal orienté horizontalement : ce type de configuration est rencontré lorsque les cristaux sont allongés (en forme de bâtonnets), et donc de grand facteur de forme
-
Une orientation de Parry correspond à une double contrainte d'orientation du cristal hexagonal : l'axe principal horizontal et deux des faces rectangulaires horizontales. Cette double contrainte forme des halos de type particuliers
Histogramme
Si l'affichage de celui-ci est demandé, l'histogramme affichera la répartition lumineuse autour du Soleil ou autour du zénith en fonction de la distance angulaire.
Ceci peut être pratique pour mesurer les halos présents dans la simulation en cours, ceux-ci apparraissants comme des pics à des distances correspondantes à leur rayons. Par exemple pour
les halos à 22° et 46° :
Histogramme des halos à 22° et 46°
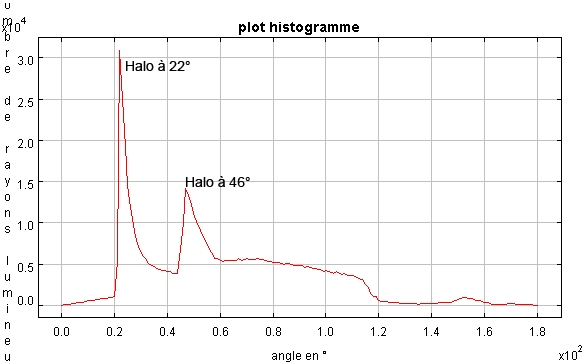
Histogramme centré sur le Soleil pour les halos à 22° et 46°, qui apparaissent comme des pics pour les angles en question
Hauteur et Azimut du centre de l'affichage
La hauteur et l'azimut du centre de l'affichage permettent de choisir dans quelle direction regarde l'observateur. La hauteur correspond à la direction haut-bas, 0 correspondant à l'horizon et 90 au zénith, l'azimut correspondant à droite-gauche, le tour complet faisant 360° et l'origine étant la direction du Soleil.
Pour centrer l'affichage sur le Soleil, il convient d'entrer un azimut de 0° et une hauteur égale à celle du Soleil ; pour centrer sur le zénith, la hauteur doit être de 90° (la valeur de l'azimut n'a alors pas d'importance)
Les cercles
Les cercles permettent d'avoir des repères de dimension sur la projection. Il est possible de les centrer où on veut (même conventions que ci-dessus) et le choix du pas permet de les afficher plus ou moins resserrés.
Il faut cocher la case "afficher les cercles" pour activer cet affichage.
Pour mesurer un halo, on pourra ainsi centrer les cercles sur le Soleil ou le zénith selon le cas, et ajuster la taille des cercles afin d'obtenir les dimensions du halo visualisé.
Des cercles de pas 90° centrés sur le zénith permettent de matérialiser l'horizon.
Afficher le Soleil
La case " afficher le Soleil " a simplement pour effet d'afficher sur la simulation un cercle jaune dont le rayon correspond à celui du Soleil
Cacher sous l'horizon
La case " cacher sous l'horizon " permet de masquer la partie de l'affichage située sous l'horizon, en remplaçant celle-ci par du bleu foncé.
Réinitialiser
La case " réinitialiser " dont il a déjà été question plus haut commande d'effacer l'image au lancement de la simulation suivante.
Nombre de rayons
Le nombre de rayons calculés entre chaque actualisation de l'affichage peut être réglé via ce paramètre. Un nombre de 1000 ou 10000 est correct pour des ordinateurs courants.
Un nombre trop faible ralentira le programme en l'obligeant à actualiser trop souvent, alors qu'un nombre trop élevé nécessitera d'attendre longtemps entre chaque actualisation.
Choix du type d'affichage
Deux types d'affichage sont proposés : l'affichage avec histogramme et l'affichage seul.
La première option affichera une petite image du halo (256 pixels de large) et un histogramme représentant la répartition lumineuse en fonction de la distance angulaire (en degrés) d'après le choix effectué par rapport à celui-ci dans les options.
L'affichage seul quant à lui affichera simplement l'image du halo sur une image de 512 pixels.
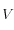 la position de l'observateur (choisi comme centre du repère)
la position de l'observateur (choisi comme centre du repère)
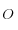 le centre de la Terre
le centre de la Terre
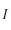 la position du cristal dans le nuage
la position du cristal dans le nuage
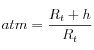 , est le rapport entre la distance des nuages au centre de la Terre et le rayon de celle-ci. Les paramètres
, est le rapport entre la distance des nuages au centre de la Terre et le rayon de celle-ci. Les paramètres 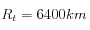 et
et 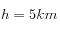 ont été choisis.
ont été choisis.
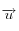 le vecteur unitaire des rayons arrivant du Soleil. Il est défini en fonction de la hauteur de celui-ci au dessus de l'horizon
le vecteur unitaire des rayons arrivant du Soleil. Il est défini en fonction de la hauteur de celui-ci au dessus de l'horizon
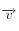 la ligne de visée de l'observateur, soit la direction du ciel dans laquelle il regarde
la ligne de visée de l'observateur, soit la direction du ciel dans laquelle il regarde
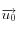 le vecteur unitaire de direction
le vecteur unitaire de direction 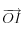


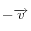
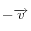
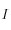 du cristal dans le ciel. Ce point est déterminé par intersection du vecteur de ligne de visée
du cristal dans le ciel. Ce point est déterminé par intersection du vecteur de ligne de visée 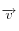 avec la sphère représentant les nuages de cristaux via la formule
avec la sphère représentant les nuages de cristaux via la formule 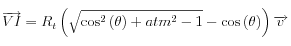 où
où 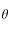 est la distance zénithale de la direction donnée par
est la distance zénithale de la direction donnée par 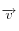
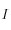 du cristal dans le ciel. Ce point est déterminé par intersection du vecteur de ligne de visée
du cristal dans le ciel. Ce point est déterminé par intersection du vecteur de ligne de visée 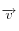 avec la sphère représentant les nuages de cristaux via la formule
avec la sphère représentant les nuages de cristaux via la formule 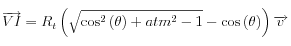 où
où 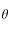 est la distance zénithale de la direction donnée par
est la distance zénithale de la direction donnée par 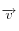
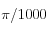 .
.
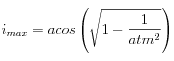 représentant l'angle sous lequel les cristaux "voient" la Terre. L'angle d'arrivée du rayon lumineux par rapport à
représentant l'angle sous lequel les cristaux "voient" la Terre. L'angle d'arrivée du rayon lumineux par rapport à 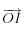 (direction de la verticale du cristal) est l'angle entre
(direction de la verticale du cristal) est l'angle entre 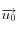 et
et 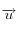 . Si cet angle est supérieur à
. Si cet angle est supérieur à 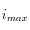 , le rayon doit être rejeté.
, le rayon doit être rejeté.

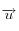 et le vecteur
et le vecteur 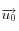 déterminant le point éclairé dans l'atmosphère. La grandeur recherché est donc simplement le produit scalaire des deux vecteurs, qui est prise comme telle en tant qu'intensité lumineuse.
déterminant le point éclairé dans l'atmosphère. La grandeur recherché est donc simplement le produit scalaire des deux vecteurs, qui est prise comme telle en tant qu'intensité lumineuse.