Réfraction, réflexion
Lois de Snell-Descartes
Un milieu transparent est caractérisé, du point de vue de son interaction avec la lumière, par son indice optique 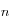 , correspondant au rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans ce milieu. Pour l'air, cet indice est proche de 1, il vaut approximativement 1.33 pour l'eau et 1.31 pour la glace.
, correspondant au rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans ce milieu. Pour l'air, cet indice est proche de 1, il vaut approximativement 1.33 pour l'eau et 1.31 pour la glace.
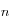 , correspondant au rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans ce milieu. Pour l'air, cet indice est proche de 1, il vaut approximativement 1.33 pour l'eau et 1.31 pour la glace.
, correspondant au rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans ce milieu. Pour l'air, cet indice est proche de 1, il vaut approximativement 1.33 pour l'eau et 1.31 pour la glace.
Lorsqu'un rayon lumineux traversant un milieu d'indice 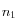 rencontre un milieu d'indice
rencontre un milieu d'indice 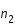 , celui-ci peut être réfracté et/ou réfléchi.
, celui-ci peut être réfracté et/ou réfléchi.
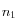 rencontre un milieu d'indice
rencontre un milieu d'indice 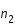 , celui-ci peut être réfracté et/ou réfléchi.
, celui-ci peut être réfracté et/ou réfléchi.
Le rayon réfléchi l'est avec un angle égal à l'angle d'incidence.
Le rayon réfracté ressort avec un angle 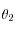 obéissant à l'équation
obéissant à l'équation 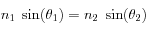 , où
, où 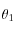 est l'angle d'incidence
est l'angle d'incidence
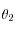 obéissant à l'équation
obéissant à l'équation 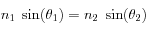 , où
, où 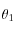 est l'angle d'incidence
est l'angle d'incidence
Si 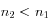 , il peut ne pas y avoir réfraction selon l'angle d'incidence, la réflexion est alors totale, le rayon étant alors intégralement renvoyé dans le milieu d'indice
, il peut ne pas y avoir réfraction selon l'angle d'incidence, la réflexion est alors totale, le rayon étant alors intégralement renvoyé dans le milieu d'indice 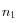 .
.
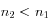 , il peut ne pas y avoir réfraction selon l'angle d'incidence, la réflexion est alors totale, le rayon étant alors intégralement renvoyé dans le milieu d'indice
, il peut ne pas y avoir réfraction selon l'angle d'incidence, la réflexion est alors totale, le rayon étant alors intégralement renvoyé dans le milieu d'indice 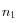 .
.
Dépendance avec la couleur
L'indice optique 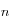 dépend de la longueur d'onde
dépend de la longueur d'onde 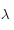 de la lumière qui éclaire le cristal. La dépendance est assez complexe, mais la loi de Cauchy donne une bonne approximation de cette dépendance dans le domaine visible. Cette formule s'écrit
de la lumière qui éclaire le cristal. La dépendance est assez complexe, mais la loi de Cauchy donne une bonne approximation de cette dépendance dans le domaine visible. Cette formule s'écrit 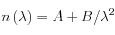 , où
, où 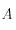 et
et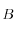 sont des constantes dépendant du milieu
sont des constantes dépendant du milieu
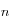 dépend de la longueur d'onde
dépend de la longueur d'onde 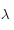 de la lumière qui éclaire le cristal. La dépendance est assez complexe, mais la loi de Cauchy donne une bonne approximation de cette dépendance dans le domaine visible. Cette formule s'écrit
de la lumière qui éclaire le cristal. La dépendance est assez complexe, mais la loi de Cauchy donne une bonne approximation de cette dépendance dans le domaine visible. Cette formule s'écrit 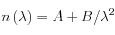 , où
, où 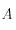 et
et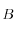 sont des constantes dépendant du milieu
sont des constantes dépendant du milieu
C'est à cause de ceci qu'un prisme éclairé en lumière blanche disperse les rayons lumineux faisant apparaître les couleurs la composant. Les halos et arcs-en-ciel présentent des couleurs pour les mêmes raisons : ce sont les gouttes d'eau ou les cristaux de glace qui jouent le rôle de prisme.
Coefficients de Fresnel
Dans le cas général, exception faite des réflexions totales, les rayons lumineux sont partiellement réfléchis et partiellement réfractés. Les coefficients de Fresnel permettent de déterminer quelle fraction du rayon incident suivra l'un et l'autre phénomène.
En outre, il existe des effets de polarisation liés à ces phénomènes, qui ne seront pas abordés ici, mais qui sont par exemple la cause de la polarisation très particulière des arcs en ciels.
Interaction de la lumière un cristal ou une goutte
Types de cristaux
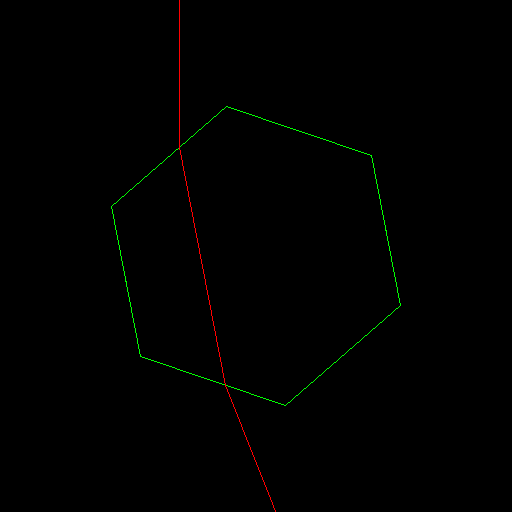
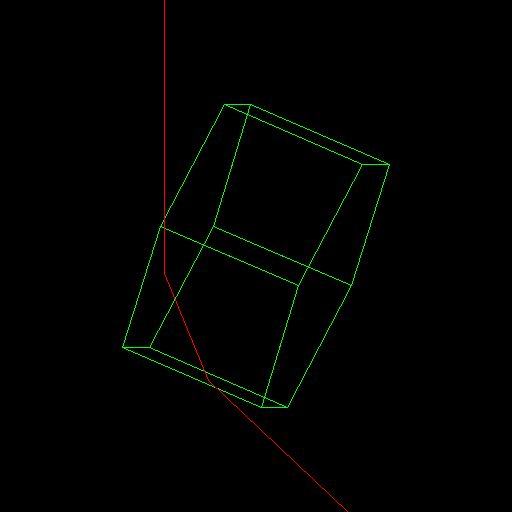
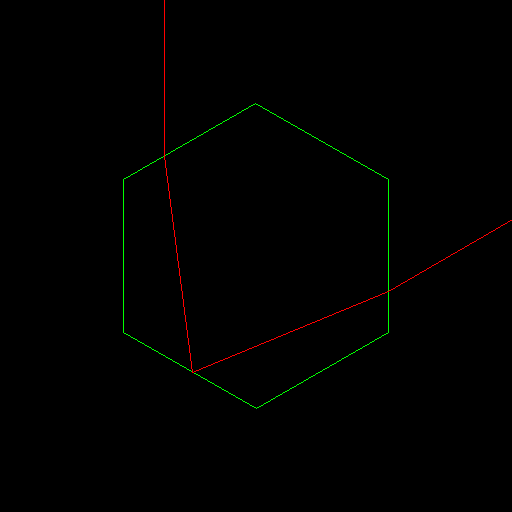
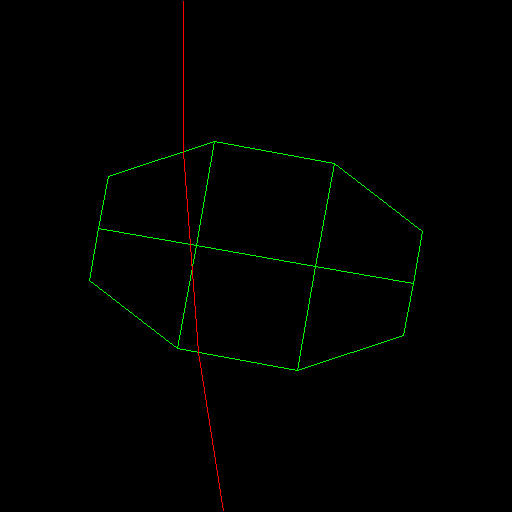
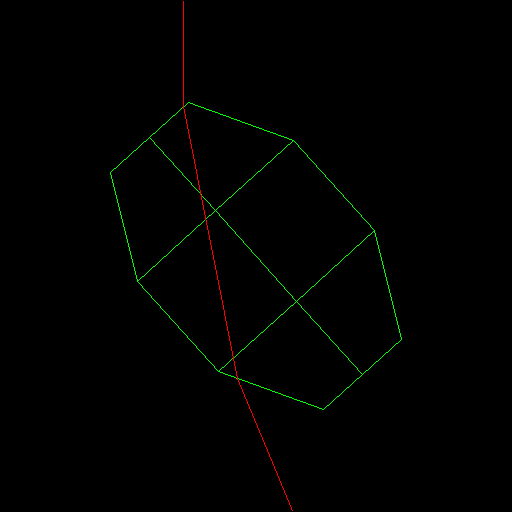
La forme des cristaux est imposée par la structure cristallographique du matériau qui les composent. On aura ainsi dans le cas de la glace d'eau des structures de type hexagonales, et dans le cas de la glace d'ammoniac, des structures bipyramidales.
La forme des cristaux résultants peut cependant être bien plus complexe lorsque les cristaux dépassent une certaine taille, on obtient alors par exemple les cristaux de glace en forme d'étoiles. Ces cristaux gardent cependant des formes liées à leur structure, ainsi on retrouve des formes hexagonales à l'intérieur de ces étoiles, d'ailleurs elles mêmes inscrites dans un hexagone.
Plus d'informations sur les cristaux de glace
Les gouttes
Le choix de la forme sphérique pour la goutte d'eau est une excellente approximation. En effet, loin d'avoir la forme telle qu'on les dessine souvent, les gouttes d'eau adoptent une forme quasi-sphérique en raison de la tension superficielle.
Elles se déforment un peu lorsqu'elles dépassent une certaine taille, dans les gouttes de pluie par exemple, mais les gouttelettes en suspension dans les nuages qui forment les arcs-en-ciel ont la forme d'une sphère
Interaction avec la lumière
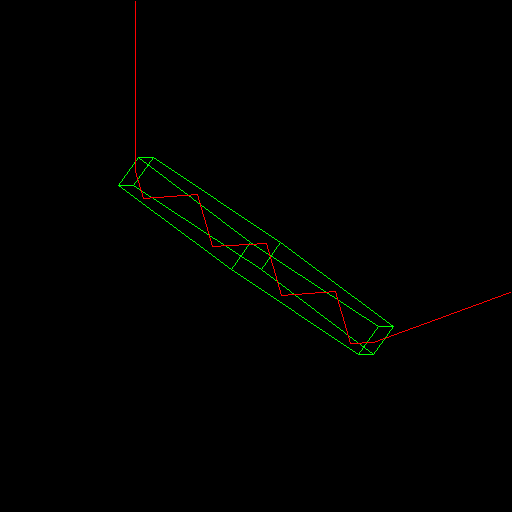
Un rayon lumineux arrivant sur une face d'un cristal ou à la surface d'une goutte de liquide va y pénétrer et être dévié, puis en ressortir par un autre endroit en étant à nouveau dévié.
Dans le cas d'un cristal, c'est l'angle entre la face d'entrée et de sortie, et dans une moindre mesure l'angle d'incidence, qui va imposer une déviation particulière au rayon lumineux, potentiellement dépendant de sa longueur d'onde. Dans le cas d'une goutte de liquide, seul l'angle d'incidence pourra jouer un rôle
On pourra en outre avoir un certain nombre de réflexions internes, totales ou non, qui auront pour effet de modifier cette déviation (essentielles pour expliquer certains phénomènes)
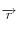 et réfractés
et réfractés 
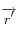 comme combinaison linéaire du vecteur directeur du rayon incident
comme combinaison linéaire du vecteur directeur du rayon incident 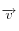 et du vecteur normal
et du vecteur normal 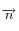 .
.
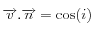 et
et 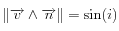 , où
, où 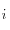 est l'angle d'incidence.
est l'angle d'incidence.
 Les formules qui en découlent sont, pour la réflexion
Les formules qui en découlent sont, pour la réflexion 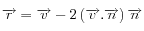 et pour la réfraction
et pour la réfraction 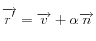 avec
avec 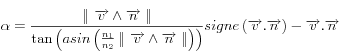
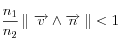
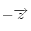 , ou
, ou 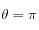 ) est généré. On cherche la première face du cristal qui sera rencontrée en cherchant quelle face, projetée dans un plan
) est généré. On cherche la première face du cristal qui sera rencontrée en cherchant quelle face, projetée dans un plan 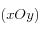 contient la projection du point source du rayon lumineux. Ceci est exécuté par la méthode in_projection_z des classes de formes géométriques.
contient la projection du point source du rayon lumineux. Ceci est exécuté par la méthode in_projection_z des classes de formes géométriques.
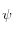 (psi) par rapport à l'axe vertical,
(psi) par rapport à l'axe vertical, 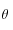 (theta) par rapport à l'axe horizontal, puis
(theta) par rapport à l'axe horizontal, puis 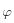 (phi) selon l'axe vertical à nouveau.
(phi) selon l'axe vertical à nouveau.