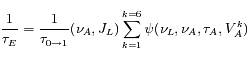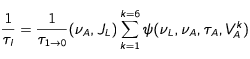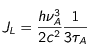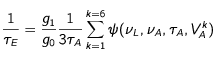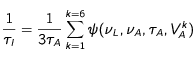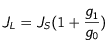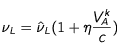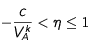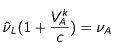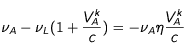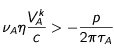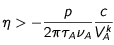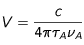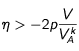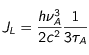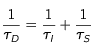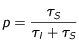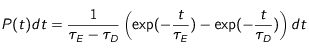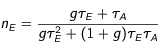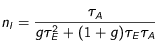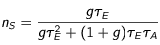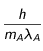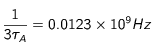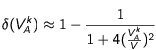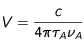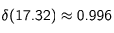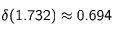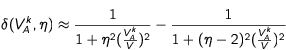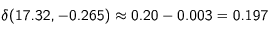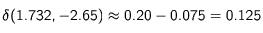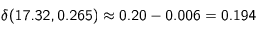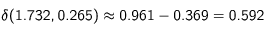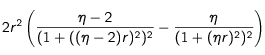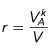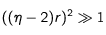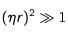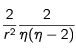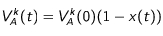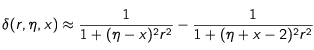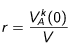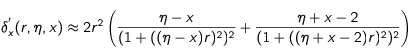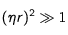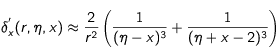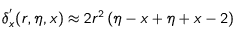Refroidissement Laser
Auteur: Laurence Simon et Jean Pierre Treuil
Date de création :
le 13 octobre 2009
Table des matières
Introduction
L'objet de ce rapport est de présenter un simulateur interactif illustrant le principe de refroidissement d'atomes par laser, dans le dispositif général d'une horloge atomique. Ce simulateur concerne plus précisément la troisième étape du dispositif de refroidissement : le ralentissement final - ralentissement "Doppler" - et le piégeage des atomes sous forme d'une "mélasse optique", physiquemment un nuage sphérique d'atomes sans paroi matérielle, de taille dont l'ordre de grandeur est le mm, très peu dense et dont la température est très près du zéro absolu.
Principe général du refroidissement
Le principe consiste à exposer au rayonnement d'un Laser un gaz d'atomes à température donnée. Chaque atome est susceptible d'être freiné suite à une séquence de deux actions : l'absorption d'un photon du laser, suivie de l'émission spontanée d'un photon.
En agissant ainsi, l'atome subit en fait deux variations de vitesse, dite de « recul » : la première en absorbant un photon « directionnel » du laser, et la deuxième, en émettant un photon dans une direction aléatoire.
Contrôler cette variation globale de vitesse c'est être en capacité de ralentir l'atome. Or, il est impossible de contrôler l'émission spontanée qui est caractérisée par un temps de désexcitation intrinsèque à l'atome, et une direction aléatoire. En revanche, il est possible de contrôler l'absorption : c'est le rôle du laser.
Contrôler l'absorption
Le laser fournit un jet collimaté de photons tous de même fréquence, se propageant tous dans la même direction et le même sens. ּ L'utilisation du laser permet d'optimiser le processus d'absorption de deux façons :
- d'une part en maximisant la probabilité d'absorption par le réglage de sa fréquence.
- d'autre part en contrôlant la direction de « recul » dû à l'absorption par le choix de son orientation,
Si le choix de l'orientation est arbitraire, à déterminer en fonction de conditions expérimentales, celui de la fréquence est imposée par la nature de l'atome : elle doit correspondre à sa fréquence d'excitation (dite de résonance) avec un décalage tenant compte de l'effet Doppler. Cet effet a deux conséquences essentielles :
- celle, contraignante, de rendre l'absorption dépendante de la vitesse de l'atome, ce qui limite le ralentissement dans le temps à un seuil minimal,
- celle, avantageuse, de rendre l'absorption dépendante du sens de déplacement de l'atome ce qui permet d'assurer le ralentissement, par le choix du sens du décalage de fréquence.
La première conséquence est due au fait qu'au delà d’un certain écart à la vitesse initiale la fréquence du laser n'est plus accordée sur celle de l'atome, et celui-ci ne peut plus absorber.
La deuxième conséquence est due au fait que le frein n'est efficace que si l'absorption a lieu alors que le sens de propagation du laser est opposé à celle du déplacement de l'atome. Dans ce cas le « recul » est opposé à la vitesse atomique, alors que dans le cas contraire, le « recul » est en fait une accélération. En choisissant une fréquence un peu inférieure à la fréquence de résonance l'absorption est largement dominante dans le sens « frein ». Une évaluation quantitative de cette dominance est développée dans
l'introduction aux exemples commentés.
L'utilisation du laser a une autre conséquence : provoquer
l'émission induite qui concurrence l'émission spontanée, pour désexciter l'atome. C'est un inconvénient majeur car une émission induite a pour effet d'annuler le recul dû à l'absorption. Il est possible d'éviter cet écueil, en jouant sur l'intensité du laser. En effet le temps caractéristique de l'émission induite est proportionnel au temps d'émission spontanée de l'atome (invariable) et à l'intensité du laser qui, elle, est modulable.
Piéger les atomes dans une mélasse optique
Dans le contexte d'une horloge atomique, la création et le maintien de la mélasse optique s'effectue en trois étapes. Dans la première étape, le gaz d'atomes est libéré par chauffage dans une enceinte, et se trouve donc initialement à une température déterminée par le processus en jeu, sublimation ou évaporation. Un dispositif technique - microtunnels dans la paroi de l'enceinte-, sélectionne les atomes dont la vitesse thermique se trouve dirigée dans une direction donnée, ce qui conduit à la formation d'un jet unidirectionnel. Dans la seconde étape, ce jet est ralenti par effet de recul consécutif aux interactions avec les photons d'un premier laser, puis dévié pour étre dirigé vers le centre d'une sphère de vide poussé. Cette seconde étape est illustrée par un simulateur accessible sur ce
lien. C'est au centre de cette sphère qu'a lieu l'étape finale de freinage et de confinement. Les atomes sont pris en charge par un dispositif de six faisceaux lasers, deux faisceaux de sens opposée dans trois directions spatiales orthogonales.
La question posée
La question posée dans cette troisième étape est donc comment transformer en quelques dizaines de nanosecondes, un jet d'atomes dont la vitesse est de l'ordre du m/s en une mélasse confinée et refroidit à quelques 10-4 K.
Shéma très simplifié du dispositif de confinement, ici en deux dimensions
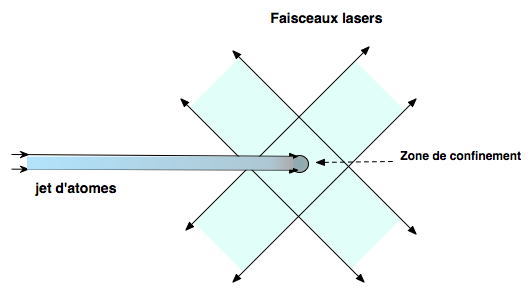
Le freinage a lieu lorsque les atomes pénètrent dans la zone de recouvrement des faisceaux. Le rayon des faisceaux est de l'ordre du cm, celui de la zone de confinement du mm.
Une application au Rubidium 87
Les données ayant servi à la construction du simulateur sont celles du rubidium (Isotope 87) , utilisé - avec le strontium et le césium - , dans les recherches sur les atomes froids. La longueur d'onde de résonnance en jeu est 780 nm, correspondant à la transition D2 entre les niveaux F1 et F2 du niveau fondamental. Dans la première étape, le gaz est chauffé 160°, et l'ordre de grandeur des vitesses sélectionnées pour la construction du jet - vitesses initiales de la seconde étape est de 100 m/s. Celui des vitesses au départ de la troisième étape est de 1 m/s
Un simulateur à événements discrets
L'originalité du simulateur est de considérer individuellement les atomes dans leurs interactions avec le flux continu des photons émis par le dispositif laser. La "vie" de chaque atome simulé est alors une succession d'excitations et de dés-excitations - spontanées ou induites- survenant à des instants aléatoires de lois de probabilités connues. Le principe de simulation est donc différent de celui adopté dans le
simulateur de l'étape antérieure, bien que
basé sur la même physique et montrant sur le temps macroscopique des dynamiques semblables. On passe bien, entre les deux simulateurs, d'une approche microscopique discontinue à une approche macroscopique continue, et cet aspect méthodologique sera repris en détail dans la section explication.
Plan du document
Ce document comporte cinq parties.
- Les objectifs du simulateur
- Le mode d'emploi de l'Applet, a savoir la présentation des différents paramètres manipulables et les écrans de résultats
- Les explications, comprenant l'exposé du modèle physique, la réalisation informatique, quelques compléments théoriques et enfin une introduction aux exemples commentés
- Deux exemples commentés
- La liste des paramètres de l'Applet
-
Objectifs
-
L'objectif du simulateur est de permettre à l'utilisateur de faire varier les paramètres du dispositif refroidissement /piégeage du jet d'atomes, pour illustrer ou estimer leurs effets, à savoir :
- le rythme moyen de ralentissement (ou refroidissement)
- l'évolution de la distribution des vitesses
- la valeur limite de la vitesse moyenne et la température équivalente
- la réalité du confinement
- la dynamique des interactions avec les photons et du niveau d'excitation des atomes
Les paramètres sur lesquels l'utilisateur est invité à jouer, pour un type d'atomes donné sont ceux caractérisant les conditions à l'entrée du dispositif et ceux caractérisant les faisceaux laser. Le rubidium 87 et sa transition à 780 nm est pris en exemple par défaut, mais les données concernant d'autres atomes ou transitions peuvent être saisies et expérimentées.
Mode d'emploi de l'applet
Le principe de l'utilisation du simulateur découle des objectifs énoncés précédemment. Les paramètres concernant les atomes sont :
- la masse
- la longueur d'onde de résonance
- le temps de désexcitation spontanée
- le rapport des poids statistique des 2 niveaux en jeu
Les conditions de conduite des simulations sont aux choix de l'utilisateur :
- le nombre d'atomes simulés
- la durée - en temps simulé - de l'observation des processus
L'utilisateur peut enfin jouer sur les caractéristiques des faisceaux lasers et les conditions d'entrée dans le dispositif :
- la fréquence des faisceaux laser
- leur intensité
- la largeur spectrale du laser
- la vitesse initiale du jet d'atomes
- la dispersion linéaire initiale des vitesses du jet d'atomes
L'utilisateur peut alors au choix visualiser, pour une simulation donnée, quatre vues centrées sur :
- l'évolution des vitesses individuelles et leur distribution
- l'évolution de la vitesse moyenne en grandeur et direction
- l'évolution du niveau d'excitation
- l'évolution du libre parcours moyen
Des explications complémentaires essentielles quant au réglage des paramètres d'entrée et quant aux vues des sorties sont données dans la section consacrée à
l'implémentation et notamment à
l'interface..
Explications
Le modèle physique
Schéma général
Le dispositif
Conme représenté dans le
schéma simplifié , un paquet d'atomes se déplaçant parallèlement avec des vitesses linéaires sensiblement identiques et déjà fortement ralentis pénètre dans une zone contrôlée par le recouvrement de six faisceaux laser, deux à deux opposés et ayant chacun la même fréquence. Dans cette zone, les atomes du paquet achèvent leur freinage, la vitesse de groupe devenant nulle, et finissent donc par être confinés dans une petite sphère au centre de la zone, dans laquelle ils s'agitent de manière quasiment thermique avec une température de l'ordre de quelques 3/10 de millikelvin.
Deux hypothèses
Le modèle physique à la base de notre simulateur repose sur deux hypothèses :
- Le paquet d'atomes considéré est optiquement mince : la proportion de l'énergie des faisceaux laser absorbée par les atomes est négligeable par rapport à l'énergie fournie par les faisceaux laser. Nous considérons que les atomes du paquet sont confrontés à une intensité de rayonnement qui est la même pour chacun d'entre eux et qui est constante dans le temps.
- La collimation, la densité, et la vitesse initiale du paquet d'atomes sont telles que le temps entre deux collisions est long par rapport à la durée simulée. Cette propriété subsiste dans la phase de confinement. Il n'y a pas non plus d'échange thermique avec un corps matériel constituant une paroi, puisqu'il n'y a pas de paroi. L'évolution du peuplement des niveaux d'énergie et le confinement résulte uniquement de l'interaction avec les photons des faisceaux laser.
Conditions initiales
Le jet d'atomes pénètre dans le dispositif dans la direction constituant la "diagonale" des trois directions orthogonales des faisceaux. Ainsi aucun faisceau n'est privilégié, la force moyenne s'exercant sur les atomes est colinéaire avec cette direction diagonale qui sera donc à priori conservée.
Un suivi individuel des atomes
Considérons un paquet constitué d'un nombre fini et donné d'atomes, dont nous suivons individuellement l'évolution. Chaque atome A est caractérisé par sa masse mA, par la fréquence de résonnance νA liée à la transition entre deux niveaux d'énergie, le délai moyen de dés-excitation spontanée τAcorrespondant. Il possède à chaque instant une vitesse vectorielle VA, dans un repère dont les trois axes correspondent à la direction des trois faisceaux, et occupe un niveau d'énergie conventionnellement pris égal à 0 pour le niveau d'énergie inférieur, et à 1 pour le niveau supérieur.
Une suite d'événements discrets
L'évolution d'un atome est une suite d'événements discrets, intervenant à des instants aléatoires et indépendants d'un atome à l'autre. Ces événements sont associés aux interactions avec le flux des photons provenant des faisceaux lasers : aborptions, dés-excitations induites ou spontanées. Chacun de ces événements - considéré comme instantané - modifie la vitesse de l'atome, en valeur absolue et en direction, ainsi que son état.
La modification des vitesses
Les formules donnant les modifications des vitesses sont les suivantes.
Pour une excitation, on additionne vectoriellement la quantité de mouvement du photon absorbé à la quantité de mouvement de l'atome :
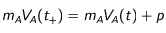
Pour une dés-excitation induite, on soustrait vectoriellement la quantité de mouvement du photon inducteur de la quantité de mouvement de l'atome :
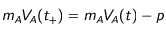
Pour une dés-excitation spontanée, on soustraie vectoriellement la quantité de mouvement de l'atome à celle du photon émis, la direction de cette dernière étant totalement aléatoire.
Interactions photons-atomes comme processus stochastiques
Taux moyens et lois de probabilités
Le délai de survenance d'un événement, qu'il soit une absorption, une dés-excitation induite ou une dés-exitation spontanée, est contrôlé, pour un état donné de l'atome, par un processus stochastique sans mémoire et uniforme. La loi de probabilité est alors la loi exponentielle paramétrée par le délai moyen de survenance, ou son inverse le taux de survenance. Il suffit donc de connaître à chaque instant les taux de survenance des événements qui s'appliquent à l'atome dans l'état ou il se trouve pour en déduire leurs lois de survenance et tirer au sort en fonction de ces lois les dates de réalisation. Les notations et équations suivantes sont inspirées des cours et ouvrages sur le transfert radiatifs cités dans la bibliographie.
Notations
Soit toujours pour l'atome, νA la fréquence du rayonnement lié à la transition entre les deux niveaux d'énergie, τA le temps moyen de dés-excitation déterminant la largeur naturelle de la raie, enfin VA sa vitesse dans la direction d'un faisceau laser contrevenant donné. Soit pour ce faisceau laser νL sa fréquence et JL son intensité. Soit g0 et g1 les poids statistiques respectifs du niveau 0 et du niveau 1.
Les expressions des taux de survenance 1) d'une excitation 1/τE d'un atome à l'état 0 et 2) d'une dés-excitation induite 1/τI d'un atome à l'état 1 sont données par les formules d'Einstein.
Expressions des taux de survenance
Réinterprétation de l'expression des taux
Les expressions des taux d'excitation et de dés-excitation peuvent se réinterpréter comme le produit d'un
taux de rencontre 1/τ d'un photon et de l'atome et d'une
probabilité d'interaction suite à cette rencontre. Taux de rencontre - différents pour l'excitation et la dés-excitation - et probabilité d'interaction sont donnés respectivement par :
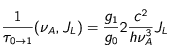
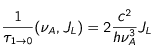
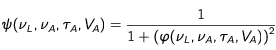
Les taux de survenance des excitations et des dés-excitations induites s'écrivent alors simplement :
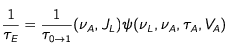
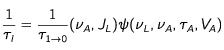
Prise en compte de l'existence des six faisceaux
Jusqu'à présent nous avons considéré les interactions de l'atome avec un seul des six faisceaux. La loi de probabilité de survenance des excitations et dés-excitations induites, en présence de tous les faisceaux est aussi une loi exponentielle dont le taux est simplement la somme des taux afférant à chacun des faisceaux pris individuellement :
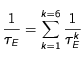
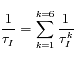
soit
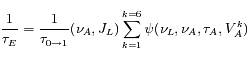
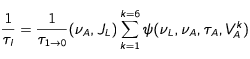
en considérant dans la somme les projections des vitesses sur chacun des six faisceaux.
Points particuliers
Choix de l'intensité
Il parait à priori assez naturel de choisir une intensité J
L assurant que les atomes excités aient le temps de se dés-exciter spontanément avant une nouvelle rencontre susceptible d'aboutir à une interaction, donc avec une valeur de la probabilité non négligeable. En se plaçant dans les conditions de départ décrites plus haut, la vitesse des atomes est telle que cette probabilité est proche de 1 dans trois directions et négligeable dans les trois directions opposées. Le choix de l'intensité doit alors être tel que le taux de rencontre
par faisceau - conduisant à une dés-excitation induite soit égal à 1/3τ
A. Ce choix conduit à une valeur de J
L égale à :
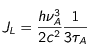
et à une expression des taux de survenance dans laquelle aucune présence explicite de l'intensité n'existe plus :
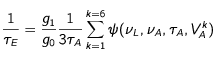
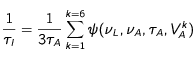
Cette valeur de l'intensité, limite au dessus de laquelle les dés-excitations induites vont dominer les dés-excitations spontanées, est en rapport avec
l'intensité de saturation J
S associée à l'atome et la transition considérée (cf Cagnac et Faroux, chap 8, p 155) :
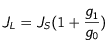
Bibliographie
Cours, Processus électromagnétiques, transfert du rayonnement et Interaction matière rayonnement. Patrick Boissé, IAP, 2008-2009.
Rutten, R.J., 2003, Radiative Transfer in Stellar Atmospheres, Utrecht University lecture notes, 8th edition. Notamment pages 19 et suivantes.
Bernard Cagnac et Jean Pierre Faroux, Lasers : interaction lumière atomes, EDP Sciences, collection Savoirs actuels, 2002. Notamment début du chapitre 8.
La réalisation informatique
Schema général
Un échéancier d'événements discrets
Le principe est celui des simulateurs d'événements discrets en temps continu. Il réside dans la gestion d'un échéancier d'événements - c.a.d d' actions modificatrices de l'état d'un atome : la boucle de base comprend donc 1) l'extraction de la prochaine échéance, 2) l'exécution de l'action associée - excitation, dés-excitation induite ou dés-excitation spontanée, enfin 3) l'inscription dans l'échéancier de la prochaine action à effectuer sur le même atome. La boucle s'arréte lorsque la date du dernier événement traité dépasse une limite fixée à l'avance et paramétrable au choix de l'utilisateur. L'initialisation de l'échéancier est effectuée par inscription des premières excitations, tous les atomes étant pris au départ désexcité.
Le calcul des échéances s'effectue à partir du fait que les lois de probabilités conditionnées par l'état des atomes, sont des lois exponentielles. Ce mode de gestion d'actions controlées par un processus stochastique en temps continu s'inspire d'une idée ancienne, voir par exemple
Gillespie 1976, reprise depuis par de nombreux travaux.
Des sorties par cycle d'actions
Les sorties du simulateur ne sont pas faites lors de chaque action, donc lors de chaque itération de la boucle. Cela augmenterai trop le temps d'exécution et serait de plus assez inutile, la modification de l'état d'un atome ne changeant que peu l'état du système, dès lors que le nombre d'atomes est suffisament grand. Nous avons fait le choix de n'effectuer des sorties qu'après avoir effectué un cycle d'actions, c.a.d après un nombre d'itérations égal à deux fois le nombre d'atomes. On peut alors considérer statistiquement que tous les atomes ont été visités, pour chacun des deux grands type d'actions.
Architecture
Les paquets
Ttois paquets sont spécifiques au simulateur : le paquet "appletlaser", le paquet "atomes et le paquet "photons". Trois autres sont généraux et peuvent servir dans d'autres applications : la paquet "espace", le paquet "classement" et le paquet "fonctions". La structure de cet ensemble de paquets est la suivante :
Hiérarchie des paquets
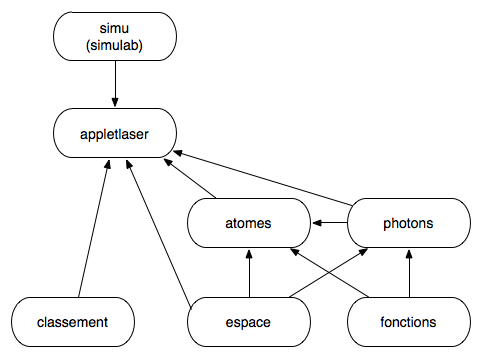
Les flèches indiquent le sens des importations. Par exemple une classe de "atomes" importe une classe de "fonctions".
- "atomes" est centré sur les données afférentes au type d'atome considéré, aux actions - ici excitations, dés-excitations induites et spontanées - qui les modifient.
- "photons" est centré sur les données du dispositif laser, le calcul des délais d'interactions des photons émis avec les atomes.
- "classement" est dédié au maintien et à l'exploitation d'un ensemble d'éléments triès selon un certain critère.
- "espace" est dédié aux opérations sur des vecteurs d'un espace à trois dimensions
- 'fonctions"est une bibliothèque de constantes, de fonctions et de tirages aléatoires. Il est aussi destiné aux opérations sur les fonctions (dérivation, intégration).
L'interface
Les paramètres d'entrée
Dans le choix des paramètres d'entrée accessibles à l'utilisateur, nous avons pris l'option d'une normalisation fixant par défaut les réglages afférents au dispositif Laser, compte tenu des données enregistrées pour les atomes : réglage de la fréquence, de l'intensité des faisceaux laser et de la largeur de leur raie spectrale.
Le réglage de la fréquence des faisceaux laser
Concernant la fréquence, nous prenons comme paramètre d'ajustement un coefficient sans dimension η , de manière à ce que la fréquence effective du laser soit donné par :
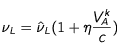
avec pour contraintes sur η
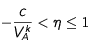
La fréquence de référence utilisée dans cette formule est définie par :
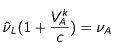
La vitesse est la projection de la vitesse
initiale du jet d'atome sur l'un des faisceaux contrevenant.
-
Une valeur nulle du coefficient η implique que la fréquence du laser perçue par les atomes soit calée sur la fréquence de résonnance.
-
Une valeur positive décale la fréquence du laser vers des valeurs plus grandes, et décale donc du même coup la fréquence perçue au delà de la fréquence de résonnance.
- Lorsque η vaut 1, la fréquence du laser est égale à la fréquence de résonnance des atomes. Les rencontres d'accélération compensent les rencontres de freinage, et la vitesse des atomes reste stable. Au delà, on observerait une accélération des atomes, ce que nous nous interdisons ici.
-
Une valeur négative décale la fréquence du laser vers des valeurs plus petites, et décale donc au contraire la fréquence perçue en deça de la fréquence de résonnance.
La différence entre la fréquence de résonnance et la fréquence perçue est donnée par :
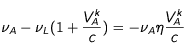
On peut estimer que cette différence ne doit pas être plus grande qu'un certain multiple
p de la largeur à mi hauteur de la raie de résonnance en fréquence. Ce qui donne un ordre de grandeur de la
limite pratique de η du coté des valeurs négatives :
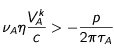
et donc
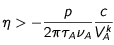
Une valeur dont nous retrouverons l'usage dans
l'introduction aux exemples commentés est la grandeur ayant la dimension d'une vitesse définie par :
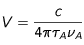
La valeur limite de η s'écrit alors
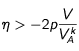
Le réglage de l'intensité des faisceaux laser
Concernant l'intensité, le paramètre d'ajustement est le rapport entre l'intensité effective et une intensité de référence. Cette intensité de référence est celle qui assure dans les conditions de départ et avec la fréquence de référence l'égalité entre le nombre moyen par atome et unité de temps de désexcitations induites et le nombre moyen, également par atome et par unité de temps, de dés-excitations spontanées, c.a.d, rappelons le
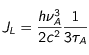
donc calculée à partir des données afférentes à l'atome.
Le réglage de la largeur spectrale des faisceaux laser
Dans les conditions expérimentales dont nous avons pris connaissance au Syrte, la largeur spectrale du laser est petite devant la largeur naturelle de la raie de l'atome. Néammoins la possibilité est ouverte d'expérimenter d'autres conditions. Aussi cette largeur du laser est prise en valeur relative, par rapport à celle de l'atome. Dans la marche du programme, elle est considérée comme nulle dès lors qu'elle est inférieure à 0.053. La valeur par défaut affichée, 0.025, équivaut donc à une largeur nulle.
Les graphes de sorties
Quatre graphes de résultats sont programmés, chacun présentant deux graphiques.
Le suivi des vitesses individuelles
Le premier est centré sur le suivi des vitesses individuelles. Dans un premier graphique est reporté à chaque date de fin de cycle la norme de la vitesse de l'atome concerné par la dernière action du cycle. Le second graphique présente la distribution des vitesses dans la population des atomes à la fin du cycle. Il visualise la fonction donnant le nombre d'atomes dont la vitesse rapportée - pour normalisation - à la vitesse médiane est inférieure à une valeur donnée. La construction de ce dernier graphique ralentissant beaucoup la simulation n'est pas effectuée à chaque cycle.
Le suivi de la vitesse moyenne
Le second est centré sur la vitesse moyenne du paquet d'atomes (premier graphique) et sa direction (second graphique). Les données sont sorties à chaque cycle. La vitesse moyenne est la norme du vecteur vitesse moyen. La direction est mesurée en degrés en prenant l'angle du vecteur vitesse moyen avec la direction initiale.
Le suivi des actions
Le troisième est centré sur la fréquence des actions subies par les atomes et leur niveaux d'énergie. Le premier graphique représente à chaque fin de cycle le nombre d'excitations efficaces, par atome et par unité de temps, tel que constaté pendant le cycle. Le second graphique présente la proportion d'atomes excités constatée à chaque fin de cycle, diminuée de la proportion d'atomes non excités fois le rapport des poids statistiques g = g1/g0, grandeur appelée différence pondérée des populations.
Le suivi des parcours
Le quatrième est centré sur les libres parcours des atomes, et complète donc le second quant à la visualisation du confinement.
Le premier graphique donne la fréquence des changements d'orientations - toutes causes confondues- telle qu'on peut la constatée sur l'état des atomes à la fin du cycle. Le second graphique donne dans les mêmes conditions la longueur du libre parcours moyen.
Points particuliers
Mention doit enfin être faite de plusieurs points concourants à la compréhension du programme et à son utilisation.
Prise en compte de la largeur spectrale du laser
La raie spectrale du laser est très fine, dans la troisième étape du dispositif de refroidissement, par rapport à celle de l'atome, et elle peut être sans inconvénient considérée comme nulle dans le simulateur. Cependant nous avons voulu offrir la possibilité d'expérimenter des valeurs plus larges. La solution adoptée est conforme à l'esprit général du simulateur : Chaque faisceau laser se trouve décomposé en un nombre fini de sous-faisceaux, chacun correspondant à une petite bande de fréquence suffisamment petite pour être considérée comme nulle du point de vue de l'atome. Chacune de ces sous-faisceaux porte ainsi une fréquence moyenne et une intensité, la somme des intensités devant être égale à l'intensité "bolométrique" du faisceau décomposé. Le calcul de l'intensité d'un sous-faisceau se fait par intégration entre les deux bornes de sa bande de fréquence, par la méthode trapézoidale, avec un pas adapté. D'autres méthodes - Hermite, Gauss, Lobato - pourraient être adoptées et insérées dans la package "fonctions".
Cette décomposition en sous-faisceaux a l'avantage de ne pas changer la structure générale du programme. Tous ces faisceaux se font concurrence de la même manière que, dans le cas d'une raie très fine, se font concurrence pour interagir avec les atomes les faisceaux non décomposé du dispositif : c'est le premier qui gagne au tirage au sort, compte tenu de ses "moyens", à savoir sa fréquence et son intensité.
Ensemble triés
Pour maintenir un échéancier d'actions dans le bon ordre des dates, de même que pour trier l'ensemble des atomes selon les vitesses, il faut disposer de méthodes adéquates. Les versions actuelles de Java permettent de maintenir des ensembles d'objets triés en permanence sur des critères choisis, mais les classes fournissant ces services n'existent pas dans la version initiale de Java. Nous avons donc recréer de telles classes, insérées dans le paquet "classement". Le choix s'est inspiré de l'idée présente dans l'algorithme
Smoothsort (Dijkstra 1981) consistant à construire et maintenir un arbre binaire d'éléments.
Tirage poissonnien sur une sphère
Pour le tirage d'un vecteur aléatoire en trois dimensions, nous avons utilisé le fait que la projection d'une sphère sur un cylindre la circonscrivant sur un de ses grands cercles - projection perpendiculaire à l'axe du cylindre - conserve les aires. Un processus ponctuel de Poisson uniforme sur le cylindre se transforme donc par la projection inverse en un processus ponctuel de Poisson uniforme sur la sphère.
Compléments
Du niveau microscopique au niveau macroscopique
Les taux paramétrant les lois de probabilités fixent du même coup certaines valeurs caractérisant macroscopiquement le paquet d'atomes et son évolution. On peut ainsi appréhender les valeurs moyennes du nombre d'événements de chaque type par atome et par unité de temps , et consécutivement la fréquence des changements d'orientations et la longueur des libres parcours. La connaissance de ces ordres de grandeurs est notamment utile pour calibrer au départ des simulations les graphiques de sorties. On peut enfin évaluer le freinage et la dimension du confinement.
Lois des délais effectifs
Les taux dont il a été question jusqu'ici sont des taux conditionnels à un état donné de l'atome ou à une cause donnée de l'événement . Pour connaître le nombre moyen des excitations et des dés-excitations, il faut remonter aux lois de probabilités contrôlant les délais effectifs entre ces événements, tous états et toutes causes confondus.
délai effectif de dés-excitation
La loi de probabilité contrôlant le délai de dés-excitation effectif, quelque soit la cause, spontanée ou induite, de cette dés-excitation, est une loi exponentielle, comme peut le montrer un calcul simple.Son taux effectif 1/τ
D est :
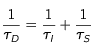
La probabilité qu'une dés-excitation induite survienne avant une dés-excitation spontanée est :
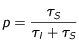
délai effectif d'excitation
La loi de probabilité contrôlant le
délai entre deux excitations successives, regroupant donc une phase où l'atome reste excité et une phase où il est dés-excité, n'est pas une loi exponentielle. La probabilité
P(t)dt que la seconde excitation survienne entre l'instant
t et l'instant
t+dt est :
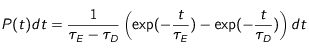
Cette loi redevient approximativement une exponentielle si l'un des délais τ
E ou τ
D domine l'autre. Le délai moyen entre deux excitations est consécutivement τ
E+τ
D, et l'écart type de ce délai est également égal à τ
E+τ
D.
Nombre moyen d'événements de chaque type
Ces constats permettent alors d'évaluer
les nombres moyens, par atome et par unité de temps, 1) d'excitations n
E, 2) de dés-excitations induites n
I, et 3 de dés-excitations spontanées n
S . Des calculs simples tenant compte de l'expression de τ
D , des égalités τ
I = τ
E(g
1/g
0), τ
S = τ
A, et enfin de l'équilibre entre les excitations et les dés-excitations et en posant g = g
1/g
0, aboutissent à :
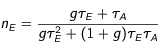
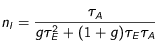
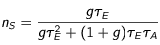
Ces formules soulignent un fait important. Lorsque l'intensité augmente pour tendre vers l'infini, τ
E diminue et tend vers 0. Le nombre d'excitations augmentent alors lui aussi indéfiniment, et le rapport entre le nombre de dés-excitations induites et le nombre d'excitations tend vers 1. Le nombre d'excitations efficaces - celles qui contribuent au freinage puis au confinement -
augmente lui aussi, mais en tendant vers une
borne supérieure finie 1/((1+g)τ
A). Dans les conditions de départ mentionnées pour les vitesses, lorsque l'on passe d'une intensité réalisant τ
I=τ
A à une intensité infinie, on augmente bien le nombre d'excitations efficaces par atome et unité de temps - et donc le freinage - mais dans un rapport de g(2+g)/(1+g)
seulement.
Changements d'orientations et libres parcours
Bien qu'au niveau d'un atome la survenue des événements d'excitations, d'émissions induites et de désexcitations ne soient pas indépendants, la somme nC = nE +nI +nS donne l'ordre de grandeur, à un instant donné, du nombre nC de changements d'orientations, et 1/nC le délai entre deux changements. L'ordre de grandeur du libre parcours moyen s'en déduit alors par produit avec la vitesse moyenne du moment.
Introduction aux exemples commentés
Le chapitre des "exemples commentés" présente deux exemples centrés sur deux vitesses initiales différentes, à savoir 30 m/s et 3 m/s, en comparant dans chaque cas la réponse du système au réglage de la fréquence laser.Pour interpréter ces exemples et réponses, il est bon d'avoir à l'esprit différentes valeurs numériques, au moins en ordre de grandeur, pour les réglages par défaut. Il est également utile de connaître qualitativement le sens de variation de ces valeurs lorsqu'on modifie ces réglages. Nous pouvons alors, en comparant les valeurs données par les équations et les calculs fait par le simulateur, valider le comportement de ce dernier. Le but des explications qui suivent, et qu'il est préférable d'aborder après la lecture des exemples d'utilisation, est de surcroît de mettre en évidence :
- l'impact de la vitesse initiale sur l'efficacité du freinage, pour un réglage donné de la fréquence laser
- la réponse du système à une perturbation plus ou moins grande de ce réglage, et ce pour différents ordres de grandeurs de la vitesse initiale
- l'évolution de l'importance du freinage dans le temps, ce pour différents ordres de grandeurs de la vitesse initiale en tenant compte du réglage
En préliminaire, il est utile de rappeler les ordres de grandeurs de la vitesse perdue et du taux de rencontre.
Vitesse perdue
La modification de la vitesse lors de la rencontre de l'atome avec un photon est :
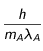
ce qui donne dans le cas du rubidium sur la transition de 780 nm la valeur de 0.00588 m/s, donc de l'ordre de 6 mm par seconde.
Taux de rencontre
Avec l'intensité choisie, le taux de rencontre d'un atome avec un photon contrevenant, est pour
un faisceau :
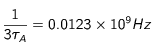
donc 12 millions de rencontres par secondes, une rencontre (par atome) toutes les 9 nanosecondes en moyenne.
Impact de la vitesse initiale sur le freinage
Le freinage, sur une certaine durée, est proportionnel à la différence entre la probabilité de rencontre avec un photon contrevenant à la direction prise par l'atome, et un photon allant dans le même sens. Au départ du processus, dans le réglage par défaut, la première probabilité est de 1, puisque ce réglage par défaut assure une fréquence perçue égale à la fréquence de résonnance. La seconde est plus petite. Un calcul simple
montre que cette différence δ est, toujours dans le réglage par défaut, et en négligeant le rapport V
A/c devant 1:
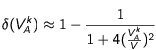
où la vitesse
V déjà mentionnée vaut
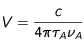
C'est la vitesse qu'il faudrait pour parcourir la longueur d'onde de résonnance en un temps 4 π τ
A. Sa valeur pour le rubidium, sur la transition de 780 nm est 2.299 m/s et son carré 5.28. Pour V
A = 30 m/s, et donc sa projection sur la direction d'un faisceau 17.32 m/s on trouve :
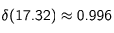
En revanche, lorsqu'on descend à 3 m/s, la différence devient :
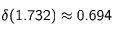
La dépendance par rapport à la vitesse devient notable pour des vitesses de l'ordre du m/s : le freinage devient moins efficace lorsque la vitesse diminue, même lorsque la fréquence percue demeure calée sur la fréquence de résonnance.
Réponse à une perturbation du réglage de fréquence
Un calcul permet d'exprimer la différence des probabilités δ en fonction de la valeur du paramètre η de réglage de la fréquence laser. On trouve, toujours en négligeant le rapport V
A/c devant 1,
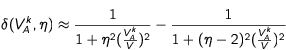
Le premier terme de l'expression représente la probabilité d'interaction avec un photon contrevenant. Le second terme est la probabilité d'interaction avec un photon venant de la direction opposée. La vitesse présente dans cette expression est toujours, rappelons le,
la vitesse initiale du paquet d'atomes. Considérons maintenant deux cas :
- En prenant une valeur négative de η telle que l'écart entre la fréquence perçue et la fréquence de résonnance soit égale à la largeur à mi hauteur de la raie de l'atome (p = 1), soit pour 30 m/s η = -0.265 et pour 3 m/s η = 2.65, on trouve :
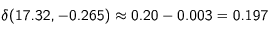
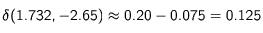
Le taux de rencontre étant de 0.0123 GHZ, cela fait une différence ente le nombre de freinages et le nombre d'accélérations, sur une direction de faisceau, de l'ordre de 2400000 par seconde pour une vitesse de 30 m/s et 1500000 par seconde pour une vitesse de 3 m/s. Ces données représentent encore des freinages importants, de l'ordre de 12 m/s en une milliseconde, qui doivent être vus comme des bornes supérieures aux freinages effectifs.
- Si maintenant on se tourne vers les valeurs positives de η, avec la même valeur de p, on trouve :
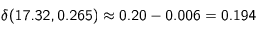
Soit pratiquement la même valeur que celle obtenue pour la valeur opposée de η. Pour 3 m/s cependant, le maintien de la même valeur de p, c'est à dire avec un écart entre la fréquence perçue d'un photon contrevenant et la fréquence de résonnance égal à la largeur à mi-hauteur de la raie, est exclu : Il conduit en effet à une valeur de η égale à 2.65, supérieure à 1, traduisant une fréquence du laser supérieure à la fréquence de résonnance et donc une accélération. En maintenant la valeur précédente de 0.265, donc en prenant un écart fréquence perçue - fréquence de résonnance égal simplement au dixième de la largeur à mi - hauteur, on trouve :
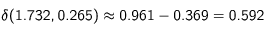
Analyse qualitative
La dérivée de la différence δ par rapport à η nous informe plus précisément sur l'impact des perturbations.
Elle s'écrit :
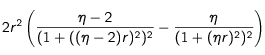
avec
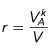
Considérons à nouveau deux cas :
-
Sur des variations infinitésimales autour de la valeur nulle du réglage : si l'écart η est suffisamment proche de 0, cette dérivée est négative ; l'intensité du freinage décroit lorsque l'écart devient positif, c'est à dire lorsqu'on augmente la fréquence du laser. Il croit au contraire lorsque il devient négatif, c.a.d. lorsqu'on diminue la fréquence du laser. La valeur nulle de l'écart, c.a.d. un calage strict de la fréquence perçue sur la fréquence de résonnace, n'est donc pas - rigoureusement - optimal. Cela s'explique intuitivement, car lorsqu'on opère en diminuant - très légèrement - la fréquence du laser par rapport à ce calage, la probabilité de rencontres accélérantes diminue plus vite que celle de rencontres décélérantes. Remarquons toutefois que ces réponses à une variation de l'écart η autour de la valeur nulle deviennent rapidement faibles lorsque les vitesses initiales sont grandes.
-
Sur des variations notables : la remarque précédente souligne un fait marginal. Plus intéressante est la conclusion que l'on peut déduire de l'expression de la dérivée dès que
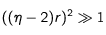
pour les valeurs positives de l'écart ou
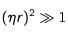
pour les valeurs négatives. La dérivée devient alors
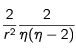
Elle change de signe lorsque l'on passe des valeurs négatives aux valeurs positives de l'écart. Si l'écart η est positif, la dérivée est négative, le freinage décroît lorsque la fréquence du laser devient encore plus forte - donc en s'écartant encore plus de la fréquence de référence- . Si l'écart est négatif, la dérivée est positive, le freinage décroît également lorsque la fréquence du laser devient encore plus faible. Pour des variations notables de la fréquence du laser, la fréquence de référence assurant le calage de la fréquence perçue d'un photon contrevenant sur la fréquence de résonnace apparait bien comme un optimum
Dynamique du freinage
Les formules données dans les paragraphes précédents correspondent aux conditions de départ, et à la vitesse initiale. Lorsque le système évolue, la vitesse moyenne diminue, et donc aussi les probabilités. Soit
x(t) le taux mesurant la diminution de vitesse par rapport à la vitesse intiale à l'instant t.
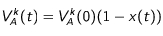
La formule donnant la différence δ des probabilités à l'instant
t, en fonction de la vitesse initiale, le coefficient η et la valeur atteinte pour x à cet instant est la suivante :
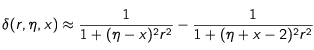
avec
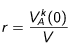
La dérivée par rapport à
x, quant à elle, vaut :
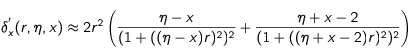
Lorsque η est nul ou négatif, cette dérivée est toujours négative.
Le freinage est de plus en plus ralenti lorsque la vitesse diminue. Lorsque le réglage est positif, les choses sont plus complexes. On doit doit considérer deux cas, selon l'ordre de grandeur de la vitesse initiale :
-
Premier cas : Considérons des vitesses de départ suffisamment grandes pour que :
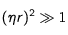
La dérivée devient alors
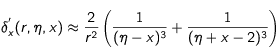
Pour un écart η positif cette dérivée est positive en x = 0 : L'intensité du freinage va commencer par croître. Puisque lorsque x est proche de 1 la dérivée est toujours négative, il y a nécessairement un point d'inflexion. On peut estimer que la position du point d'inflexion, pour des vitesses de départ grandes, ne sera pas éloigné de la valeur x = η.
-
Second cas : Lorsqu'au contraire les vitesses sont faibles, avec un rapport r proche de 0, la dérivée devient :
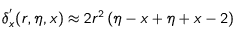
et elle reste négative pour tout x, même pour des valeurs positives de η. Aucun point d'inflexion ne s'observera.
Exemple d'utilisation
Résultats de simulation pour vitesse intiale 30 m/s
Cette vitesse initiale ne correspond pas évidemment aux conditions réelles du dispositif dans sa troisième étape, pour laquelle cette vitesse est de l'ordre du m/s. Nous le présentons cependant, à titre comparatif, en centrant sur la dynamique de la vitesse moyenne du groupe d'atomes, en norme et en direction, et la réponse aux modifications de réglage de la fréquence du laser.
L'introduction aux exemples commentés a pointé en effet sur les différences de comportement selon l'ordre de grandeur des vitesses initiales, différences dues au rapport entre le décalage nécessaire de la fréquence laser et la largeur de la raie de l'atome.
A noter que les résultats qui vont suivre ont été obtenu avec un rapport des poids statistiques (g) valant 1.
Dynamique de la vitesse moyenne
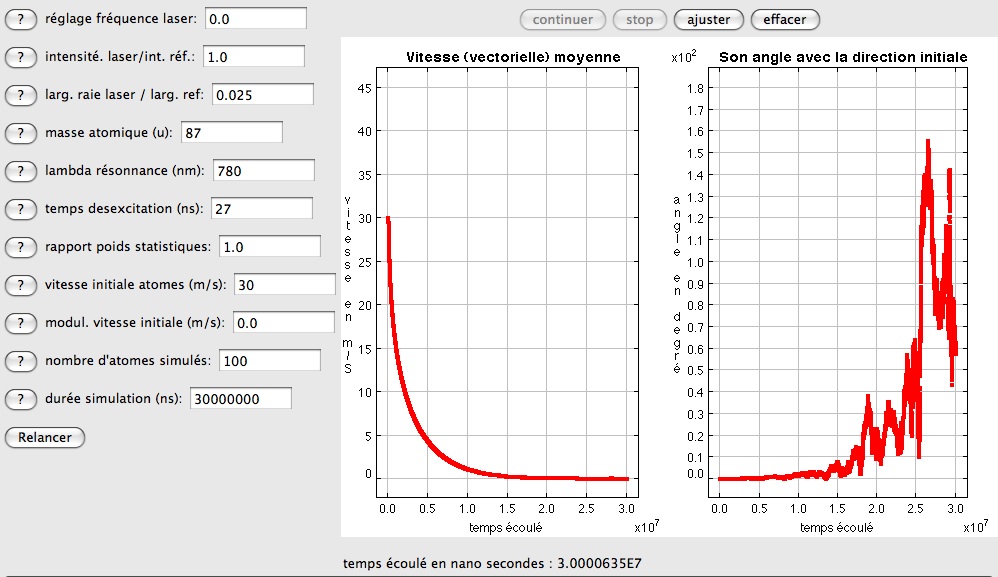
Dans le cas simulé, la fréquence perçue d'un atome contrevenant est calée sur la fréquence de résonnance. L'écart relatif à la fréquence de référence, qui assure ce calage est donc nul. La vitesse moyenne passe de 30 m/s à une vitesse proche de zéro en 15 millisecondes environ. Pendant ce temps, la direction de la vitesse du groupe reste très stable, au moins jusqu'à 10 millisecondes. Après quoi, la valeur de la vitesse se stabilise et sa direction oscille aléatoirement. Le groupe des atomes a parcouru une distance de l'ordre de 30 cm.
Réponses à une diminution notable de la fréquence du Laser
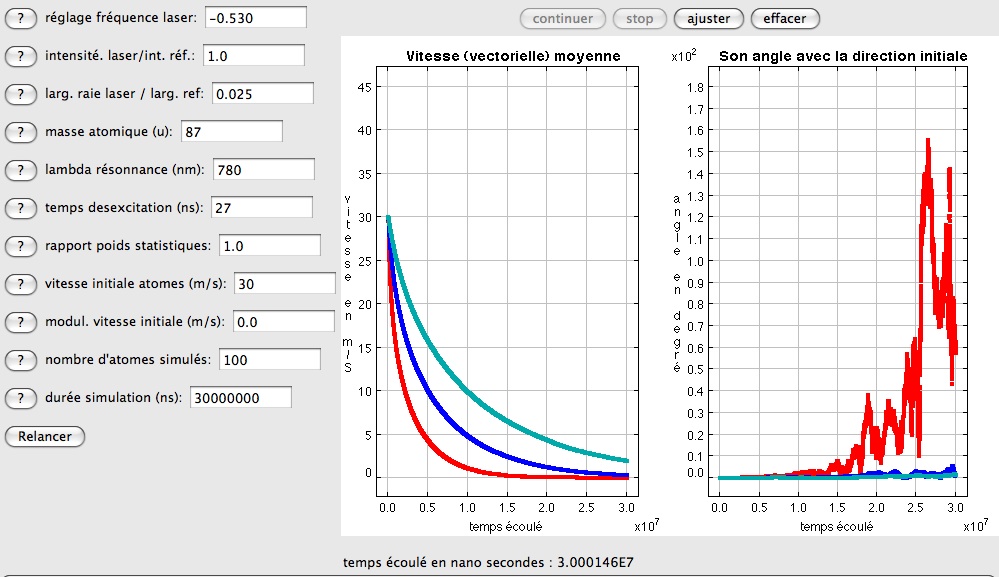
La figure suivante présente la réponse de la vitesse moyenne pour une fréquence non décalée - pour comparaison - , puis décalée négativement d'une fois, puis de deux fois la largeur à mi hauteur de la raie de l'atome (valeurs du réglage laser respectivment de -0.265 et -0.530. On constate une diminution drastique de l'intensité du freinage, qui reste cependant observable. A 30 millisecondes, le système n'est pas encore stabilisé.
Réponse à une diminution notable de la fréquence du laser
Réponses à une augmentation notable de la fréquence du Laser
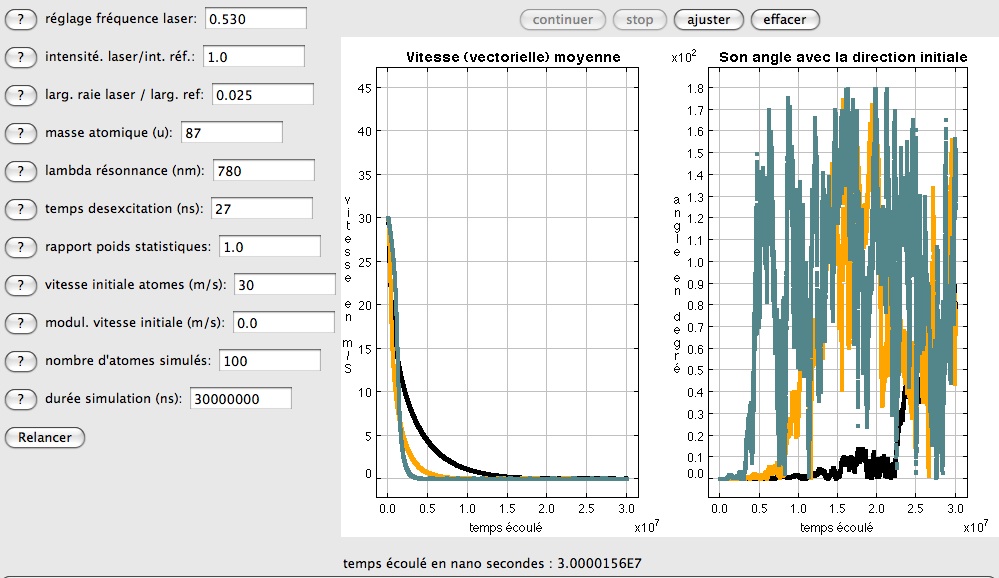
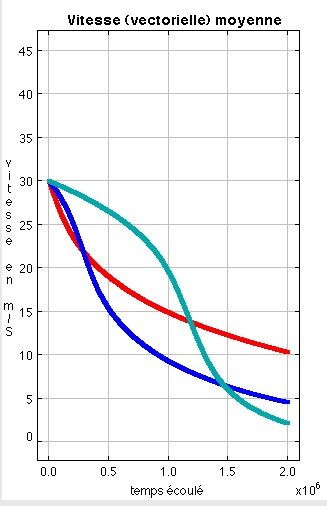
La figure suivante présente le cas symétrique d'un décalage positif de la fréquence, toujours d'une fois, puis de deux fois la largeur à mi hauteur de la raie. On constate que le freinage part d'une valeur plus faible, mais augmente progressivement en intensité. La dynamique de la vitesse présente un point d'inflexion. Ce comportement fait qu'au total, le groupe d'atomes se stabilise plus tôt, l'instant de la stabilisation étant de l'ordre de 5 millisecondes. Le principe de ce gain est de "prendre de l'avance". On atteint le maximum de l'intensité du freinage pour une vitesse déjà réduite notablement. La seconde figure montre un zoom sur le début du processus, montrant la position des points d'inflexion, survenant à des vitesses de 22 et 15 m/secondes environ. Bien entendu, ce gain disparait lorsque la fréquence du Laser devient trop décalée, puisque pour la valeur maximale admise pour le décalage positif, amenant la fréquence du laser sur la fréquence de résonnace, la vitesse moyenne du groupe reste parfaitement constante.
Réponse à une augmentation notable de la fréquence Laser
Zoom sur les deux premières millisecondes
Un paradoxe ?
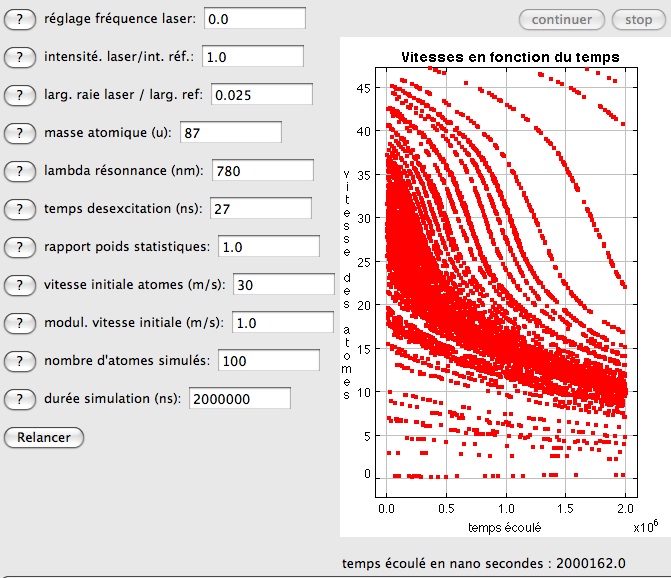
Un tel résultat peut surprendre, lorsqu'on se rappelle que pour une fréquence de laser donnée, le freinage ne dépend que de la vitesse atteinte. De fait, les courbes individuelles des atomes d'un groupe ne se recoupent jamais, même en présence d'inflexion, comme le montre la figure suivante. Dans cette figure, les vitesses de départ sont dispersées fortement, et celles qui sont au dessus de la vitesse moyenne de 30 m/s présentent un point d'inflexion. Mais la fréquence du laser est pour toutes la même. Dans le cas précédent au contraire, la vitesse de départ est la même, mais la fréquence du laser est différente pour chaque courbe.
Evolution des vitesses individuelles d'un groupe d'atomes
Retour sur le confinement
L'étude du libre parcours moyen, en liaison avec la dynamique des vitesses et la fréquence des changements d'orientations, permet d'affiner le confinement. La baisse de la fréquence des changements d'orientations, du à l'écart croissant entre la fréquence perçue d'un photon contrevenant et la fréquence de résonnance, tend à augmenter le libre parcours moyen. A contrario, la diminution des vitesses tend à réduire le libre parcours. La combinaison de ces deux tendances contradictoires abouti au résultat présenté çi après; On y constate d'abord une augmentation du libre parcours, atteignant la dizaine de micromètres en ordre de grandeur, pour redescendre en fin de parcours à 500 nm environ.
Dynamique du libre parcours moyen
Résultats de simulation pour 3 m/s
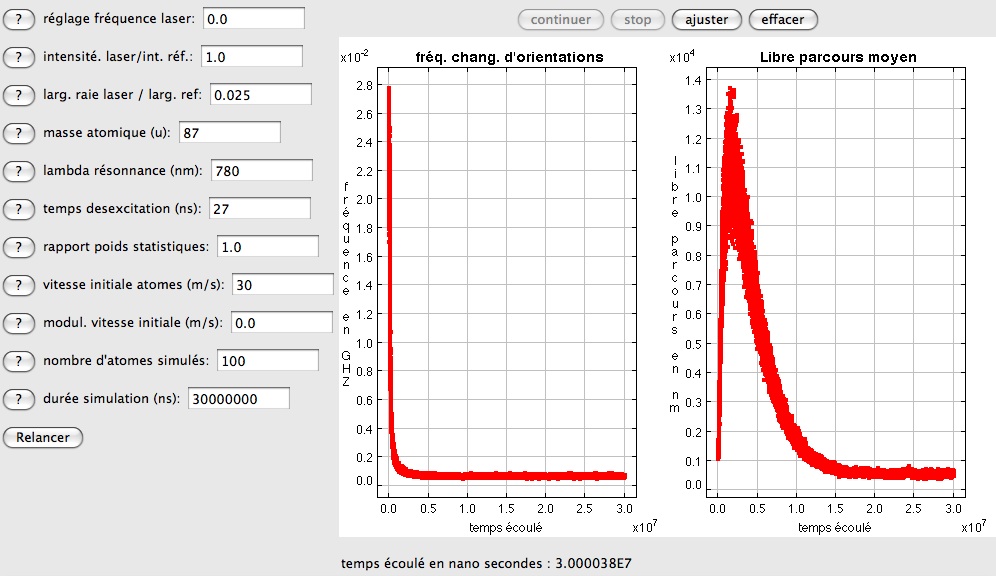
Le comportement de la vitesse moyenne du groupe, pour une fréquence perçue d'un photon contrevenant calé sur la fréquence de résonnance, est donnée dans la figure çi après. On y observe une stabilisation du groupe d'atomes à une vitesse moyenne nulle après un temps d'environ 0.5 millisecondes, la distance parcourue étant donc de l'ordre du mm.
Dynamique de la vitesse moyenne
Réponses à une diminution notable de la fréquence Laser
La dynamique est semblable à celle présentée pour 30 m/s. Pour une fréquence décalée négativement d'une fois, puis de deux fois la largeur à mi hauteur de la raie de l'atome (valeurs du réglage -2.65, -5.30),on constate bien une diminution drastique de l'intensité du freinage, qui reste cependant observable.
Réponses à une augmentation notable de la fréquence du laser
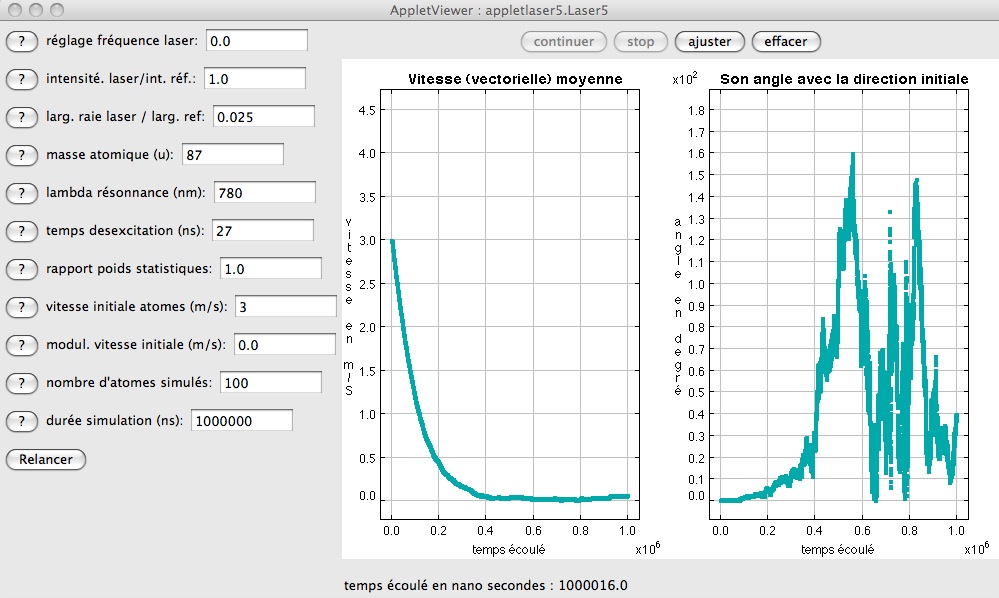
Nous avons pris trois décalages croissants de la fréquence perçue au delà de la fréquence de résonnance, compatibles avec la basse valeur de la vitesse initiale. Ces décalages sont respectivement de respectivement de 1/10, de 2/10 et de 3/10 de la largeur à mi hauteur de la raie, correspondant à des valeurs de réglage de 0.265, 0.530, 0.795 ; on observe une dégradation, au début peu prononcée, de l'intensité du freinage. Aucune inflexion n'est visible.
Réponse à une augmentation de la fréquence du laser
Evaluation du confinement
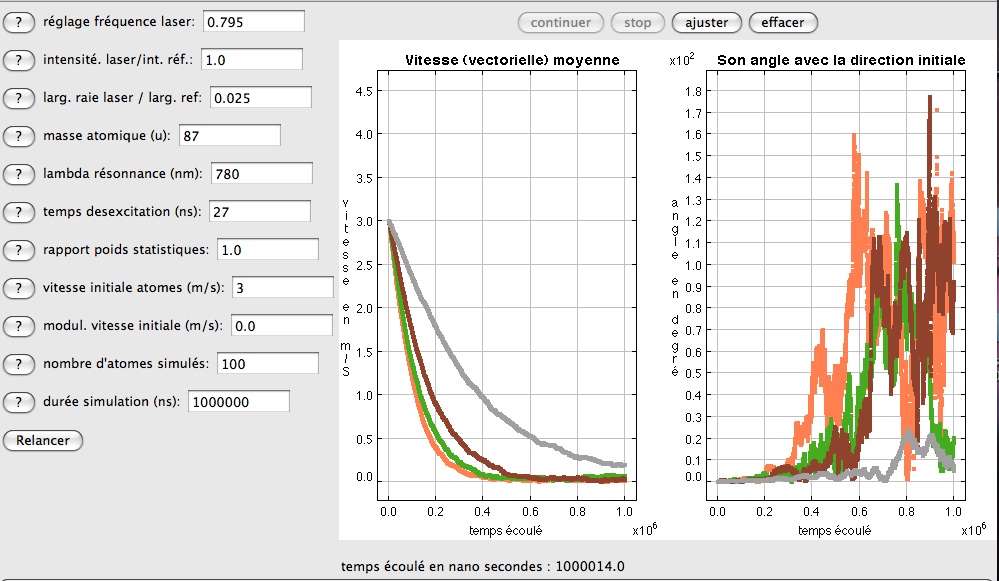
La dynamique du confinement montre une décroissance continue du libre parcours moyen, qui part de la centaine de nanomètres, au début du processus, pour se stabiliser à 10 nanomètres environ. Le temps de stabilisation est du même ordre que celui constaté pour la vitesse moyenne, entre 200 et 600 microsecondes. La fréquence des changements de direction est alors de 2.9 107 GHZ, soit un délai moyen entre deux changements d'orientation - toutes causes confondues - de 35 nanosecondes. Avec une vitesse résiduelle linéaire de l'ordre de 0.3 m/s, on retrouve bien l'ordre de grandeur du libre parcours moyen atteint lors de la stabilisation. Il faut noter dans l'interprétation de ces graphiques que l'épaisseur des traits ne s'interprète pas comme une variabilité individuelle à un instant précis, mais comme une variabilité au cours du temps de la moyenne sur le groupe d'atomes de la grandeur étudiée.
Dynamique du libre parcours moyen
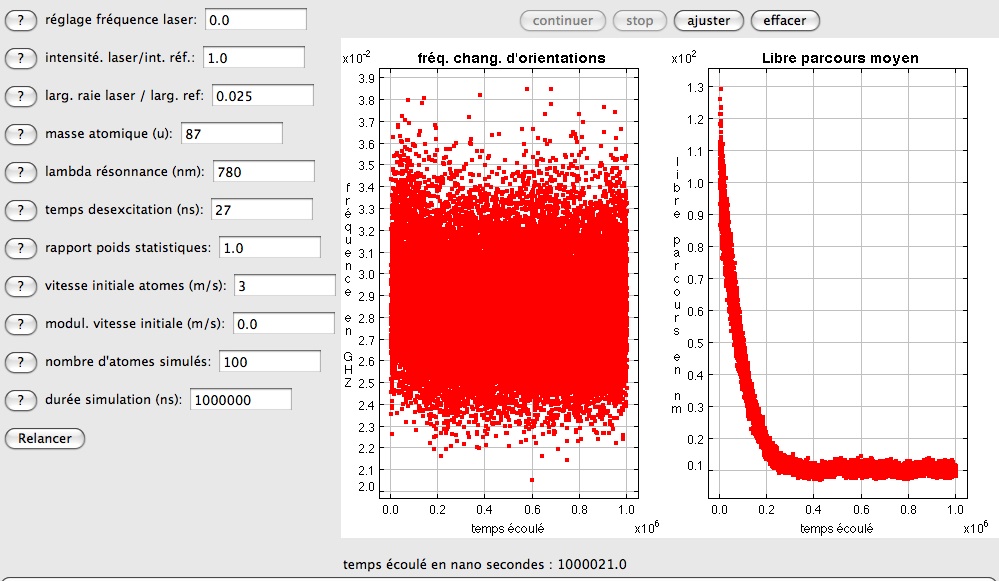
Evaluation de la distribution des vitesses
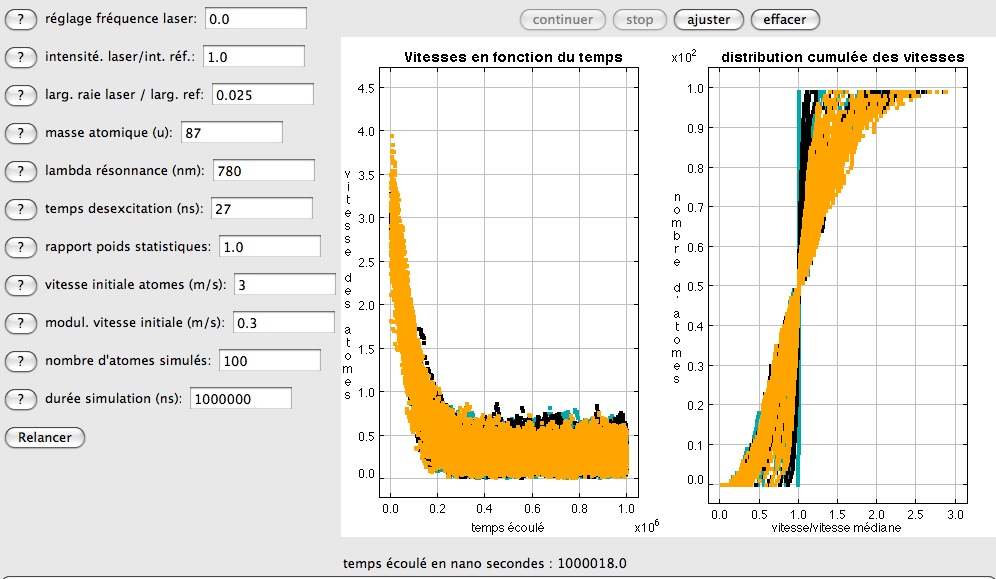
La dynamique des vitesses individuelles linéaires et de leur distribution est donnée par la figure çi après. On constate une fois la stabilisation atteinte, une relativement forte dispersion résiduelle des vitesses linéaires, s'étalant - ici pour 100 atomes - entre 0 m/s et 0.75 m/s environ. La fenètre donnant la distribution cumulée montre l'évolution de cette distribution depuis l'instant de départ, - où toutes les vitesses sont égales - jusqu'à la fin de la simulation, où elle s'est stabilisée. La dernière courbe montre une nette disymétrie, l'écart entre la vitesse maximale et la vitesse médiane étant deux fois plus grand que l'écart entre la vitesse médiane et la vitesse minimale. Il serait intéressant de superposer à cette dernière courbe celle de la distribution maxwellienne de même moyenne et écart type. La dernière figure montre enfin que la présence d'une dispersion des vitesses linéaires au départ du processus - ici de 2 m/s à 4 m/s - n'a pas d'influence sur le résultat final, le processus perdant la mémoire de cette dispersion initiale.
Dynamique de la distribution des vitesses
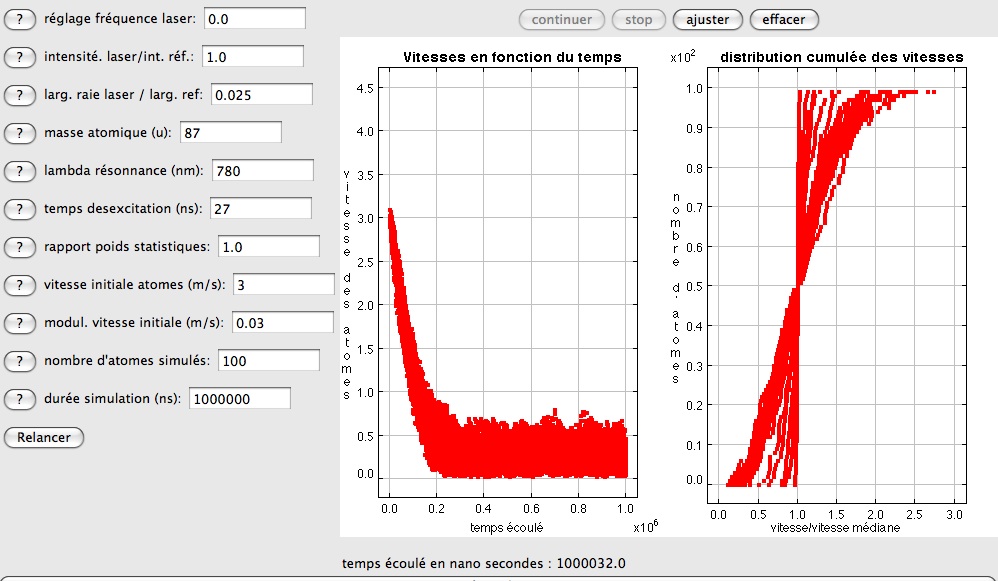
La perte de mémoire de la dispersion initiale
Liste des paramètres d'entrée de l'applet
-
titre : réglage fréquence laser
label : frequencelaser
écart relatif entre la fréquence du laser et celle qui assure l'égalité entre la fréquence perçue d'un atome contrevenant et la fréquence de résonnance.
-
titre : intensité. laser/int. réf.
label : intensitelaser
rapport entre l'intensité commune aux six faisceaux lasers et une intensité de référence.
-
titre : larg. raie laser / larg. ref
label : largeurlaser
rapport entre la largeur, à mi hauteur, de la raie du dispositif laser et la largeur à mi hauteur de la raie des atomes
-
titre : masse atomique
label : masseatome
unités : u
masse individuelle des atomes
-
titre : lambda résonnance
label : lambdatome
unités : nm
longueur d'onde de résonnance des atomes
-
titre : temps desexcitation
label : tauatome
unités : ns
temps moyen de desexcitation spontanée, déterminant la valeur du coefficient d'Einstein d'émission spontanée
-
titre : rapport poids statistiques
label : g1surg0
Poids statistique du niveau 1 rapporté au poids statistique du niveau 0
-
titre : vitesse initiale atomes
label : vitessemoy
unités : m/s
vitesse linéaire initiale moyenne des atomes
-
titre : modul. vitesse initiale
label : modulationvitesse
unités : m/s
norme d'une modulation gaussienne de la vitesse linéaire des atomes autour de leur vitesse moyenne.
-
titre : nombre d'atomes simulés
label : nbatomes
nombre d'atomes simulés
-
titre : durée simulation
label : dureesim
unités : ns
durée totale de la simulation
Liste des paramètres de sortie de l'applet
-
titre : temps écoulé
label : temps
unités : ns
-
titre : vitesse des atomes
label : vitesseat
unités : m/s
-
titre : nombre d'atomes
label : rang
-
titre : vitesse/vitesse médiane
label : vitesse
-
titre : temps écoulé depuis le début
label : tempsecoule
unités : ns
-
titre : nombre d'excitations
label : nbexcitations
unités : par atome et par ns
-
titre : proportion d'atomes excités
label : nbexcites
-
titre : vitesse en m/S
label : vitvecmoy
-
titre : angle en degré
label : vitprjmoy
unités : degres
-
titre : fréquence en GHZ
label : freqmoy
unités : GHZ
-
titre : libre parcours en nm
label : lpm
unités : nm


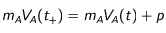
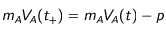
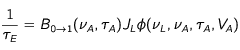
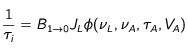
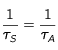
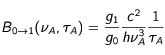
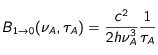
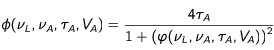
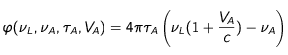
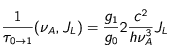
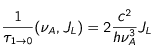
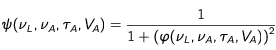
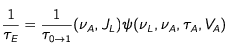
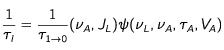
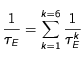
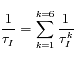 soit
soit