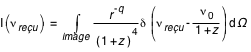Le spectre.
On souhaite maintenant calculer le spectre intégré du disque vu depuis l'observateur. On suppose que chaque point du disque à la distance r émet une raie infiniement fine centrée sur
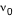
avec la luminosité
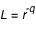
(ce qui est bien évidemment un modèle simpliste). Du point de vue de l'observateur que nous sommes, le spectre est donc donné par :
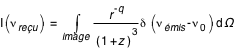
Il faut transformer cette expression afin de l'exprimer en fonction de
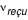
, la fréquence mesurée par l'observateur. Or on sait que
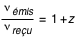
. On en déduit donc, en utilisant le changement d'échelle dans un Dirac :
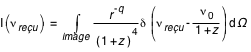
Ce modèle bien que simpliste doit permettre d'obtenir l'allure du spectre bien connu avec deux pics (ce calcul n'est pas encore implémenté dans les applets qui illustrent cet exposé).

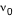 avec la luminosité
avec la luminosité 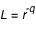 (ce qui est bien évidemment un modèle simpliste). Du point de vue de l'observateur que nous sommes, le spectre est donc donné par :
(ce qui est bien évidemment un modèle simpliste). Du point de vue de l'observateur que nous sommes, le spectre est donc donné par :
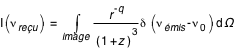
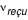 , la fréquence mesurée par l'observateur. Or on sait que
, la fréquence mesurée par l'observateur. Or on sait que 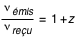 . On en déduit donc, en utilisant le changement d'échelle dans un Dirac :
. On en déduit donc, en utilisant le changement d'échelle dans un Dirac :